Цели работы: ознакомиться с методами планирования эксперимента; научиться составлению центральных композиционных планов 2-го порядка и обработке результатов эксперимента; решить приведенную задачу.
Краткие теоретические сведения
Центральное композиционное планирование используют в тех случаях, когда кривизна поверхности отклика велика и не может быть адекватно описана многочленом первого порядка. Наиболее широко для описания таких поверхностей применяют полиномы второго порядка типа
. (1)
Общий вид матрицы планирования для композиционного 2-фактор-ного плана представлен в табл. 1.
Таблица 1
Композиционный план 2-го порядка для 2 факторов
| Системы опытов | № оп. | х 0 | х 1 | х 2 | х 1 х 2 | х 12 | х 22 |
| Полный факторный эксперимент | +1 | +1 | -1 | -1 | +1 | +1 | |
| +1 | +1 | +1 | +1 | +1 | +1 | ||
| +1 | –1 | +1 | –1 | +1 | +1 | ||
| +1 | –1 | –1 | +1 | +1 | +1 | ||
| Опыты в звездных точках | +1 | +a | a2 | ||||
| +1 | –a | a2 | |||||
| +1 | +a | a2 | |||||
| +1 | –a | a2 | |||||
| Опыты в центре плана | +1 | ||||||
| ... | ... | ... | ... | ... | ... | ... | |
| N | +1 |
Здесь х 1и х 2 – нормированные значения первого и второго факторов, a – величина звездного плеча.
Геометрически план второго порядка для двух факторов можно представить в виде рисунка.
Количество опытов в матрице композиционного плана второго определяется по формулам
при k < 5; 
, при k ³ 5, (2)
где 2 k – число опытов, образующих полный факторный эксперимент (ядро плана); 2 k – число так называемых звездных точек в факторном пространстве, имеющих координаты (±a, 0); (0, ±a); n 0 – опыты в центре плана. Различают два вида композиционного планирования – ортогональное и ротатабельное.
Рис. Композиционный план 2-го порядка для 2 факторов
Ортогональный план второго порядка
В общем виде композиционные планы второго порядка не ортогональны, но они легко приводятся к ортогональным выбором соответствующего звездного плеча a. Значения звездного плеча a для ортогонального композиционного плана приведены в приложении 7.
Пример ортогонального плана второго порядка для двух факторов приведен в табл. 2.
Таблица 2
Ортогональный план 2-го порядка для 2 факторов
| Системы опытов | № оп. | х 0 | х 1 | х 2 | х 1 х 2 | х 1* | х 2* |
| Полный факторный эксперимент | +1 | –1 | –1 | +1 | +1/3 | +1/3 | |
| +1 | +1 | –1 | –1 | +1/3 | +1/3 | ||
| +1 | –1 | +1 | –1 | +1/3 | +1/3 | ||
| Опыты в звездных точках | +1 | +1 | +1 | +1 | +1/3 | +1/3 | |
| +1 | +1 | +1/3 | –2/3 | ||||
| +1 | –1 | +1/3 | –2/3 | ||||
| +1 | +1 | –2/3 | +1/3 | ||||
| +1 | –1 | –2/3 | +1/3 | ||||
| Опыты в центре плана | +1 | –2/3 | –2/3 |
Уравнение регрессии при центральном ортогональном композиционном планировании ищут в следующем виде:
. (3)
Благодаря ортогональности матрицы планирования все коэффициенты регрессии определяются независимо друг от друга по формулам
(4)
; 
здесь j – номер фактора; i – номер опыта; j ¹ 0 при коэффициенте bj и j ¹ u при коэффициенте bju.
Входящие в уравнение (3) вспомогательные переменные определяются по формуле
, где 
. (5)
Расчет вспомогательных переменных производится с целью приведения матрицы к ортогональному виду. Для того чтобы получить уравнение регрессии в обычной форме
, (6)
b 0 определяют по формуле
(7)
и оценивают с дисперсией, равной
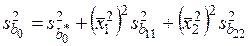. (8)
Рассчитав дисперсию воспроизводимости, проверяют значимость коэффициентов и адекватность полученного уравнения.
Коэффициенты уравнения регрессии, получаемые при помощи ортогональных планов второго порядка, определяются с разной точностью. Ошибки коэффициентов для k < 5 определяются по формулам
. (9)
. (10)
. (11)
. (12)
где u, j = 1, 2, 3, 4; u ¹ j; значения дисперсии воспроизводимости и стандарта определяются по формулам
, (13)
где 
– значения параметра оптимизации в параллельных опытах; m – количество параллельных опытов; 
– среднее значение параметра оптимизации в параллельных опытах.
Значимость коэффициентов регрессии определяется по критерию Стьюдента
. (14)
Коэффициент значим, если tj > t т, где t т – табличное значение критерия Стьюдента, которое определяется по приложению 4 в зависимости от числа степеней свободы воспроизводимости. Незначимые коэффициенты исключаются из уравнения без пересчета.
Проверка адекватности уравнения регрессии осуществляется с помощью критерия Фишера
. (15)
Здесь дисперсия адекватности определяется по формуле
, (16)
где 
– экспериментальное и расчетное значение параметра оптимизации; L – количество значимых коэффициентов уравнения регрессии.
Уравнение адекватно, если расчетное значение F меньше табличного для выбранного уровня значимости р.
Ротатабельный план второго порядка
Ортогональные планы второго порядка не обладают свойством ротатабельности. Бокс и Хантер предложили считать оптимальными ротатабельные планы второго порядка. Пример ротатабельного плана второго порядка для двух факторов приведен в табл. 3.
Определение коэффициентов уравнения регрессии при ротатабельном планировании осуществляется по формулам (17).
 ;  ;  ;  ;
 ;
 .
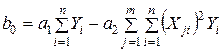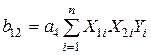| (17) |
Таблица 3
Ротатабельный план второго порядка для k = 2
| Системы опытов | № оп. | х 0 | х 1 | х 2 | х 1 х 2 | х 12 | х 22 |
| Полный факторный эксперимент | +1 | –1 | –1 | +1 | +1 | +1 | |
| +1 | +1 | –1 | –1 | +1 | +1 | ||
| +1 | -1 | +1 | –1 | +1 | +1 | ||
| +1 | +1 | +1 | +1 | +1 | +1 | ||
| Опыты в звездных точках | +1 | –1,412 | +2 | ||||
| +1 | +1,412 | +2 | |||||
| +1 | –1,412 | +2 | |||||
| +1 | +1,412 | +2 | |||||
| Опыты в центре плана | +1 | ||||||
| +1 | |||||||
| +1 | |||||||
| +1 | |||||||
| +1 |
Значения констант для определения коэффициентов регрессии при ротатабельном планировании приведены в табл. 4.
Таблица 4
Значения констант для определения коэффициентов регрессии
| Число факторов, k | Число опытов, N | n 0 | a | a 1 | a 2 | a 3 | a 4 | a 5 | a 6 | a 7 |
| 1,412 | 0,2 | 0,1 | 0,125 | 0,25 | 0,1251 | 0,0187 | 0,1 | |||
| 1,682 | 0,166 | 0,0568 | 0,0732 | 0,125 | 0,0625 | 0,0069 | 0,0568 | |||
| 2,0 | 0,1428 | 0,0357 | 0,0417 | 0,0625 | 0,0312 | 0,0037 | 0,0357 | |||
| 5* | 2,0 | 0,1591 | 0,0341 | 0,0417 | 0,0625 | 0,0312 | 0,0028 | 0,0341 | ||
| 2,378 | 0,0988 | 0,0191 | 0,0231 | 0,0312 | 0,0156 | 0,0015 | 0,0191 |
* полуреплика
Дисперсия воспроизводимости 
при ротатабельном планировании определяется по опытам в центре плана аналогично ортогональному планированию. Ошибки коэффициентов определяются по формулам (18).
Sb 02 = a 1 ; Sbj 2 = a 3 ; Sbuj 2 = a 4 ; Sbjj 2 = (a 5 +a 6) . (18)
Значимость коэффициентов уравнения регрессии определяется аналогично ортогональному планированию. Если незначимым оказался один из квадратичных эффектов, после его исключения коэффициенты уравнения регрессии необходимо пересчитать.
Дисперсию адекватности определяют по формуле
, (19)
где остаточная дисперсия, число степеней свободы остаточной дисперсии и число степеней свободы дисперсии адекватности соответственно равны:
 ,
| (20) | |
 ,
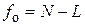| (21) | |
 .
| (22) |
Уравнение адекватно, если расчетное значение критерия Фишера не превышает табличного (приложение 8), взятого для степеней свободы f 1 = f ад и f 2 = f вос.
Задача
По результатам экспериментов получить уравнения регрессии, определить их адекватность и построить расчетные поверхности отклика в области проведения экспериментов.
Ход работы:
1. Получить исходные данные у преподавателя.
2. Определить коэффициенты уравнения регрессии по ортогональному плану эксперимента по формулам (4).
3. Определить дисперсию воспроизводимости и стандарт по формулам (13).
4. Определить ошибки коэффициентов по формулам (9–12).
5. Рассчитать значения критерия Стьюдента по формуле (14) и определить значимость коэффициентов уравнения регрессии. Скорректировать уравнение регрессии с учетом отброшенных коэффициентов.
6. Рассчитать по формуле (15) критерий Фишера и по приложению 8 определить адекватность полученной модели.
7. Построить расчетную поверхность отклика в области проведения эксперимента.
8. Аналогично (п. 1–7) получить уравнение регрессии по ротатабельному плану, определить его адекватность и построить поверхность отклика.
9. Написать вывод по работе.
Приложение 1
