Электронного осциллографа
Цель работы: изучить явление магнитного гистерезиса.
Приборы и принадлежности: кассета ФПЭ-07/02, низкочастотный генератор, осциллограф.
Описание установки
Лабораторная работа проводится на установке, состоящей из кассеты ФПЭ-07/02, генератора и осциллографа, собранной по схеме (рисунок 7.5).
| Om |
| pF |
Рисунок 7.5 – Схема установки
Принцип работы установки основан на явлении гистерезиса, возникающего в ферромагнетиках. Исследуемым образцом является сердечник тороидального трансформатора из марганец–цинкового феррита М2000НМ размерами 31×18,5×7 мм, с двумя обмотками (число витков первичной обмотки N1 = 200, число витков вторичной обмотки N2 = 50). Первичная обмотка подключается к генератору, вторичная обмотка (измерительная) подключается к осциллографу, на экране которого воспроизводится петля гистерезиса исследуемого образца. В цепи, состоящей из намагничивающей обмотки, генератора сигналов и резистора R1, создается переменный ток (напряжение 2–5 В, частота 700–806 Гц, гнезда Х1, Х2). Используемый железный образец имеет форму тора, его намагничивание осуществляется с помощью кольцевой обмотки (рисунок 7.6). Если радиус тора R0 значительно превышает радиус его поперечного сечения r0 (сердечник имеет форму тонкого кольца), то магнитное поле, существующее в обмотке, явлется однородным всюду внутри неё. При этом силовые линии имеют форму окружностей, общий центр которых совпадает с ценром тора.
|
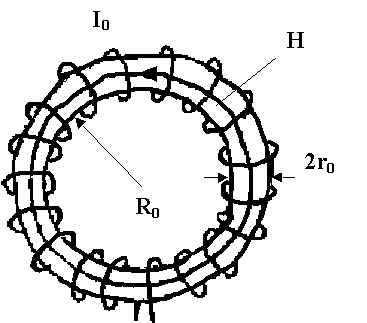
Рисунок 7.6 – Исследуемый образец, сердечник трансформатора
Поскольку вектор напряжённости магнитного поля всюду параллелен поверхности образца, то из граничных условий для векторов магнитного поля следует, что значения 
внутри и вне образца равны между собой. Это обстоятельство позволяет при выполнении расчётов не делать сложных поправок на геометрическую форму образца и существенно упрощает определение магнитной проницаемости железа. Связь между силой тока в обмотке I0 и напряженностью создаваемого этим током магнитного поля 
можно найти с помощью теоремы о циркуляции вектора :
, (7.3)
где интегрирование приводится по окружности, проходящей внутри тора (вдоль линии вектора 
), N – число витков обмотки, NI0 – полный ток проводимости, охватываемый контуром интегрирования. Из выражения (7.3) следует:
, (7.4)
где n – количество витков обмотки, приходящейся на единицу длины тора. Таким образом, напряженность магнитного поля однозначно определяется силой тока в намагничивающей обмотке и линейной плотностью ее витков.
На резисторе R1 возникает напряжение, пропорциональное току в первичной обмотке и напряженности магнитного поля в образце. Этот сигнал подается на вход «Х» осциллографа. Измерительная обмотка трансформатора присоединена к интегрирующей R2C1– цепочке.
При изменении потока внешнего магнитного поля, пронизывающего измерительную катушку, в ней возникает Э.Д.С. индукции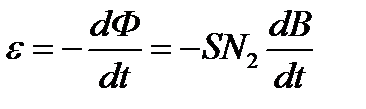 
, где S – площадь поперечного сечения тора. В случае гармонического изменения силы тока зависимость магнитной индукции от времени можно записать в виде 
, где w – циклическая частота переменного тока. Следовательно, во вторичной обмотке действует Э.Д.С. индукции 
. При этом напряжение на интегрирующей емкости С1 пропорционально индукции магнитного поля:
,
где 
– сила тока во вторичной обмотке,
– импеданс вторичной обмотки.
Этот сигнал подается на вход «Y» осциллографа (гнездо Х2, Х3).
Из выражения 
находим индукцию магнитного поля
, (7.5)
где S – площадь поперечного сечения тороидального сердечника, N2 – число витков вторичной обмотки. При получении формулы (7.5) мы пренебрегаем реактивным сопротивлением вторичной обмотки.
Падение напряжения на сопротивлении R1 равно 
и пропорционально отклонению электронного луча по горизонтали. Из этого выражения находим напряженность магнитного поля:
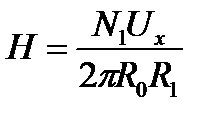, (7.6)
где N1 – число витков в первичной обмотке, R0 – радиус тора (рисунок 7.6).
Ход работы
1 Подключите к кассете ФПЭ-07/02 генератор и осциллограф (рисунок 7.5).
2 Запишите в таблицу 7.1 исходные данные схемы, которые указаны на лицевой панели кассеты.
| R1 | R2 | C1 | S | N1 | N2 | Ux | Uy | H | B | BH | B0 | Hk | mмакс |
Таблица 7.1 – Исходные и опытные данные
3 Выполните калибровку осциллографа по оси X и запишите его чувствительность по оси Х – Ux (В/дел), а также по оси Y – Uy (В/дел), которую показывает указатель соответствующей ручки.
4 Включите генератор и осциллограф в режиме выключенной развертки. Добейтесь, чтобы петля гистерезиса находилась в центре экрана, была симметричной, имела насыщение и занимала большую часть экрана.
5 Нарисуйте координатную сетку экрана осциллографа (в масштабе одна клетка - 2 см) и на нее нанесите график полной петли гистерезиса.
6 Уменьшая выходное напряжение генератора, получите семейство не менее пяти уменьшающихся до точки петель. Снимите для каждой из них координаты вершин Ux0 и Uy0. По полученным точкам постройте кривую намагничивания.
7 Используя масштабы Ux, Uy иформулы (7.5) и (7.6), найдите по графику петли гистерезиса и запишите в таблицу 7.1, значения магнитных параметров BH, B0, Hk (рисунок 7.4) для пяти петель гистерезиса.
8 Используя кривую намагничивания, по формуле 
вычислите магнитную проницаемость при различных значениях напряженности магнитного поля. Запишите в таблицу 7.1 максимальную магнитную проницаемость ферромагнетика mmax.
Тема 8
