1 Взаимная индуктивность катушек
2 Способы взаимного включения катушек
3 Коэффициент связи двух индуктивно связанных катушек
Основные понятия по теме
Каждый из контуров, по которому течет переменный ток, создает в окружающем пространстве переменное магнитное поле. В соответствии с законом электромагнитной индукции Фарадея, в других контурах, находящихся в магнитном поле, индуцируются электродвижущие силы, которые влияют на силу тока в этих контурах.
Следовательно, контуры оказываются взаимосвязанными посредством электромагнитной индукции.
Полный магнитный поток, пронизывающий k -й контур, можно записать в виде
, (5.1)
где 
– индуктивность k -го контура, при k ≠ i – взаимная индуктивность k -го контура, и i -го контура, общее число проводников равно N, Ii – сила тока в i -ом контуре. Для силы тока в k -ом контуре из закона Кирхгофа следует уравнение
, (5.2)
где Rk – активное сопротивление k -го контура, 
εк – сторонняя Э.Д.С. в этом контуре.
Подставляя выражение (5.1) в (5.2), получаем систему уравнений
. (5.3)
Чтобы решить данную систему уравнений относительно токов Ik, необходимо знать собственные индуктивности Lkk и Lki, которые играют роль постоянных коэффициентов в системе уравнений (5.3). Эти индуктивности зависят от формы, взаимного расположения и геометрических параметров контуров. Определение индуктивностей представляет собой самостоятельную задачу.
В случае двух катушек, когда одна из них одета на другую, причем обе катушки имеют общую ось, система (5.3) принимает вид
, (5.4)
Одна катушка подключена через активное сопротивление R1 к внешнему источнику напряжения
, (5.5)
где ε0 – амплитуда входного напряжения, ω – его частота. Другая катушка подключена к измерительному прибору. Пренебрегая влиянием вторичной обмотки на ток в первичной обмотке, а также самоиндукцией контуров и учитывая, что во вторичной обмотке действует только Э.Д.С. индукции, из системы (5.4) получаем
Решая систему уравнений (5.6), находим силу тока в первичной обмотке
,
и напряжение во вторичной обмотке
.
В свою очередь, напряжение в первичной обмотке равно 
. Это позволяет выразить коэффициент взаимной индуктивности катушек следующим образом:
. (5.7)
Если поменять местами катушки L1 и L2,то коэффициент взаимной индуктивности катушек, соответственно, будет равен
, (5.8)
где f – частота генератора, 
и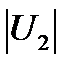 
– амплитуды напряжения на первой и второй катушках, измеренные осциллографом, М21 – коэффициент взаимной индуктивности катушки 2 по отношению к катушке 1, который равен коэффициенту взаимной индуктивности катушки 1 по отношению к катушке 2 – М12, т. е. М = М21 = М12.
Взаимная индуктивность – коэффициент пропорциональности между током, протекающим по одной катушке, и магнитным потоком сквозь витки другой катушки.
Направление магнитных полей зависит от направления намотки катушки, поэтому на схемах начала обмотки обозначают звездочкой (*) или (.). Если токи в обеих обмотках направлены относительно помеченных зажимов, то такое включение катушки называется согласным, при этом магнитные потоки самоиндукции и взаимной индукции складываются, коэффициент взаимной индукции М является величиной положительной. Если катушки включены так, что потоки самоиндукции и взаимной индукции имеют различные знаки, то такое включение называется встречным. М при этом является величиной отрицательной.
Пусть длинный тонкий соленоид длиной l с площадью поперечного сечения S содержит N1 витков плотной намотки. Поверх него изолированным проводом плотно намотана катушка с N2 витками. Вычислим взаимную индуктивность М.
Индукция магнитного поля внутри соленоида 
. Магнитный поток через каждый виток катушки 2 равен:
.
Теперь получаем:
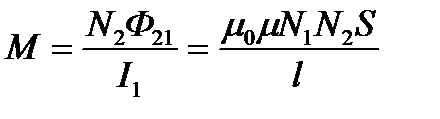, (5.9)
Здесь 
– магнитная постоянная, μ – относительная магнитная проницаемость сердечника.
Выясним соотношение между индуктивностями двух индуктивно связанных катушек одинаковой длины, размещённых на тороидальном сердечнике, и их взаимной индуктивностью М. Первичная катушка имеет индуктивность
, (5.10)
индуктивность второй катушки равна
. (5.11)
Перемножив равенства (5.10) и (5.11) и извлекая корень квадратный из полученного выражения, находим
. (5.12)
В общем случае, при наличии магнитного рассеяния,
, (5.13)
где К – коэффициент связи двух индуктивно связанных катушек.
Найдём К опытным путём. Задаём произвольное напряжение на входе U1, измеряем напряжения на выходе U2 и берём их отношение 
. Аналогичным образом находим коэффициент передачи 
. Затем коэффициент связи К находим из выражения
. (5.14)
Вопросы для самоконтроля
1 Напишите и объясните формулу закона Фарадея для соленоида, помещённого в изменяющееся магнитное поле.
2 Объясните понятия «магнитный поток», «магнитный поток через площадь, ограниченную витком», «взаимная индуктивность катушек».
3 Отчего зависит взаимная индуктивность катушек?
4 Какое из соединений катушек называется согласным, а какое встречным?
5 Приведите примеры определения коэффициента связи в различных цепях.
Лабораторная работа 5
