1*. Множество точек называется выпуклым, если
1 – оно является многоугольником;
2 – оно вместе с любыми двумя своими точками содержит весь отрезок, соединяющий эти точки;
3 – большинство точек отрезка принадлежит данному множеству;
4 – отрезок, соединяющий любые две несовпадающие точки множества, целиком принадлежит этому множеству.
2. Функция называется выпуклой, если
1 – она является строго вогнутой;
2 – она определена на выпуклом множестве W;
3 – она определена на выпуклом множестве W и выполняется условие 
для любых точек х1,х2 Î W и для любого t Î [0,1];
4 - она определена на выпуклом множестве W и выполняется условие F(αX1 + (1-α/2)X2) ≤ αF(X1) + (1-α/2)F(X2) для любых точек х1,х2 Î W и для любого t Î [0,1].
3. Функция называется гладкой, если
1 – непрерывны ее первые производные;
2 – непрерывны ее первая и вторая производные;
3 – на переменные наложено условие неотрицательности.
4. Какая функция имеет локальный максимум?
1 – если в окрестностях точки Х* выполняется неравенство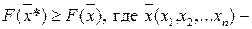 
любая точка, принадлежащая окрестности любого, в том числе бесконечно малого радиуса;
2 – если в окрестностях точки Х* выполняется неравенство 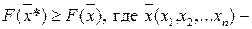любая точка, принадлежащая области определения функции;
3 – если в окрестностях точки Х* выполняется неравенство 
любая точка, принадлежащая окрестности любого, в том числе бесконечно малого радиуса.
5. Какая функция имеет абсолютный максимум?
1 – если в окрестностях точки Х* выполняется неравенство 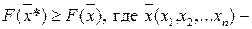любая точка, принадлежащая окрестности бесконечно малого радиуса;
2 – если в окрестностях точки Х* выполняется неравенство 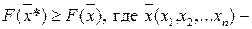любая точка, принадлежащая области определения функции;
3 – если в окрестностях точки Х* выполняется неравенство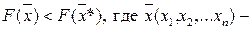 
любая точка, принадлежащая определенному множеству.
6. Задача называется выпуклой, если она имеет
1 – выпуклую целевую функцию;
2 – выпуклую систему ограничений и выпуклую целевую функцию;
3 – выпуклую целевую функцию и нелинейную систему ограничений;
7. «Если область D замкнута и ограничена, то дифференцируемая функция
z = f(x) достигает в этой области своего наибольшего или наименьшего значений или в стационарной точке, или в граничной точке области».
1 – теорема Ляпунова;
2 – теорема Неймана;
3 – теорема Вейерштрасса;
4 – теорема Лагранжа.
8*. Градиентные методы:
1 – наискорейшего подъема;
2 – штрафных функций;
3 –наискорейшего спуска;
4 – локального случайного поиска;
5 – нелокального случайного поиска.
9. В чем отличие метода локального случайного поиска от метода нелокального случайного поиска?
1 – в формировании случайного вектора 
;
2 – в формировании случайного вектора
;
3 – в ограничении количества проводимых испытаний;
4 – в задании начального вектора Х0.
10*. В чем отличие метода штрафных функций при решении задачи выпуклого программирования и задачи линейного программирования?
1 – определяется число М для задания функции штрафов, формируется массив случайных чисел, находится функция штрафов, определяется конечное число неудачных испытаний;
2 – задаются числа Мj для задания функции штрафов для каждого ограничения, формируется массив случайных чисел, находится функция штрафов, определяется конечное число неудачных испытаний;
3 – для задачи линейного программирования штрафные функции подбираются так, чтобы избежать узких гребней, затрудняющих применение методов поиска безусловных экстремумов;
4 – параметр М в процессе решения задачи меняется от малой величины до большой.
11. Все методы решения, основанные на исследовании функций в небольшой окрестности последовательно выбираемых точек, называют
1 – методами отсечения;
2 – методами поиска;
3 – методами возможных направлений;
12. Градиентом функции называется
1 – вектор, проекциями которого на координатные оси служат соответствующие частные производные, т.е. Ñ F = 
;
2 – вектор, направление которого указывает скорость убывания функции в этой точке;
3 – отрезок, ограничивающий область определения функции.
13. Функция называется сепарабельной, если
1 – ее можно представить в виде суммы функций, каждая из которых зависит только от одной переменной;
2 – ее можно представить в виде квадратичной функции;
3 – она содержит константу.
14*. Приближенное решение задач выпуклого программирования градиентным методом заключается
1 – в задании «выгодного» направления приближения к оптимальному решению;
2 – в нахождении оптимального решения за наименьшее число шагов;
3 – в поиске точки начального приближения;
4 – в нахождении приближенного значения оптимального решения в определенной области решения.
15*. Градиентный метод называется «методом наискорейшего спуска», если
1 – величина длины шага выбирается так, что приращение функции при перемещении из точки Х0 в точку Х1 будет наибольшим при решении задачи на минимум;
2 – величина длины шага выбирается так, что приращение функции при перемещении из точки Х0 в точку Х1 будет наименьшим при решении задачи на минимум;
3 – величина длины шага выбирается так, что приращение функции при перемещении из точки Х0 в точку Х1 будет наименьшим при решении задачи на минимум и наибольшим при решении задачи на максимум.
16. Для задач выпуклого программирования справедлива теорема: необходимым и достаточным условием оптимальности вектора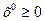 
является существование вектора 
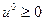такого, что пара 
будет седловой для соответствующей функции Лагранжа, т.е. 
при всех , .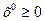
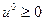1 – теорема двойственности;
2 – теорема Лагранжа;
3 – теорема Куна–Таккера;
4 – теорема Эйлера.
