Дифференциальное уравнение вида
. (12)
где 
– заданные непрерывные функции от x или постоянные, называется линейным дифференциальным уравнением первого порядка.
Его характерным признаком является наличие лишь первых степеней функции 
и ее производной 
. Если 
, то линейное уравнение называется неоднородным. Если 
, то уравнение
. (13)
называется линейным однородным.
Для решения неоднородных линейных уравнений можно использовать: 1) метод Бернулли, или метод подстановки (аналогично тому, как это делалось для однородного относительно переменных x и y уравнения первого порядка); 2) метод вариации произвольных постоянных, или метод Лагранжа, который может быть также использован и для интегрирования линейных дифференциальных уравнений более высоких порядков.
Рассмотрим первый метод подстановки.
Будем искать решение неоднородного линейного уравнения в виде
. (14)
Для удобства аргумент x в дальнейшем будем опускать. Тогда 
. Подставляя (14) в уравнение (12), получим
;
.
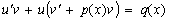Если функцию 
выбрать как некоторое решение уравнения с разделяющимися переменными 
(или однородного линейного уравнения), то исходное уравнение примет вид 
.
Подставляя найденное решение в данное уравнение, получим уравнение с разделяющимися переменными относительно переменной x и функции u(x). Если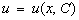 
– общее решение полученного уравнения, то общее решение исходного линейного уравнения (12) примет вид: 
, или окончательная формула для определения имеет вид:
.
Таким образом, интегрирование линейного уравнения (12) сводится к решению двух уравнений с разделяющимися переменными, одно из которых является однородным.
Замечание. Если вместо 
и подставить полученное после интегрирования значение, то получим, что общее решение линейного, уравнения (12), равное сумме общего решения соответствующего однородного линейного уравнения (13) и частного решения неоднородного линейного уравнения (12).
Примеры:
8. 
.
Решение:
Будем искать решение уравнения в виде произведения двух функций: 
. После этой подстановки данное уравнение примет вид: 
.
Вынесем за скобки u: 
Найдем одну из функций v, такую, чтобы выражение в скобках обратилось в нуль: 
. Это уравнение будет с разделяющимися переменными. Решим его. 
Подставим найденную функцию в уравнение, найденное раньше.
.
Т.к. y = uv, то 
- общее решение данного уравнения.
9. 
.
Решение:
.
Теперь для u (x) получим: 
, и общее решение уравнения 
.
Для нахождения частного решения, соответствующего начальным условиям задачи Коши, подставим в общее решение 
.
Откуда получаем частное решение: 
.
Рассмотрим второй метод Лагранжа.
Метод вариации произвольных постоянных (метод Лагранжа) состоит в следующем.
1) Составляется однородное линейное уравнение (13) соответствующее неоднородному линейному уравнению (12) за счет замены правой части 
на ноль. Это уравнение легко проинтегрировать как уравнение с разделяющимися переменными. Его решением является функция
,
где C – произвольная постоянная.
2) Общее решение неоднородного линейного уравнения можно найти исходя из общего решения соответствующего однородного уравнения, варьируя произвольную постоянную, т.е. полагая, что
,
где 
– некоторая, подлежащая определению, дифференцируемая функция от x.
Для нахождения нужно подставить в исходное уравнение, что приводит к уравнению с разделяющимися переменными
,
которое имеет следующее решение:
,
где A – произвольная постоянная. Тогда искомое общее решение линейного неоднородного уравнения примет вид
.
Как несложно заметить, полученное решение совпадает с решением, найденным методом Бернулли.
Пример:
10. Решить уравнение 
Решение:
Разделим уравнение на xy2: 
Полагаем 
.
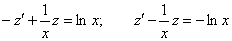Полагаем 
Произведя обратную подстановку, получаем:
11. Решить уравнение 
Решение:
Разделим обе части уравнения на 
: 
Полагаем 
Рассмотрим соответствующее ему линейное однородное уравнение:
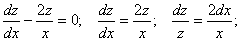
Полагаем C = C(x) и подставляем полученный результат в уравнение, с учетом того, что:
Получаем: 
Применяя обратную подстановку, получаем окончательный ответ: 
.
