Пусть на отрезке [ a, b ] (b > a) задана непрерывная функция y = f (x), принимающая на этом отрезке неотрицательные значения: 
при 
. Требуется определить площадь S криволинейной трапеции ABCD, ограниченной снизу отрезком [ a, b ], слева и справа - прямыми x = a и x = b, сверху – функцией y = f (x). 
Для решения этой задачи разделим произвольным образом основание AD фигуры точками x 0 = a, x 1 , x 2 , …, xn -1 = a, xn = b на n частей [ x 0 , x 1], [ x 1 , x 2], …, [ xi -1 , xi ], …, [ xn -1 , xn ]; символом 
будем обозначать длину i -го отрезка: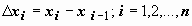 
. На каждом из отрезков [ xi -1 , xi ] выберем произвольную точку 
, найдём 
, вычислим произведение 
(это произведение равно площади прямоугольника Pi с основанием [ xi -1 , xi ] и высотой ) и просуммируем эти произведения по всем прямоугольникам. Полученную сумму обозначим S ступ: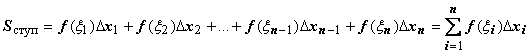 
.
S ступ равно площади ступенчатой фигуры, образованной прямоугольниками Pi, i = 1,2,…, n; на левом рисунке эта площадь заштрихована. S ступ не равна искомой площади S, она только даёт некоторое приближение к S. Для того, чтобы улучшить это приближение, будем увеличивать количество n отрезков таким образом, чтобы максимальная длина этих отрезков 
стремилась к нулю (на рисунке ступенчатые фигуры изображены при n = 7 (слева) и при n = 14 (справа)). При 
разница между S ступ и S будет тоже стремиться к нулю, т.е.
.
Пусть на отрезке [ a, b ] задана функция y = f (x). Разобьём отрезок [ a, b ] произвольным образом на n частей точками [ x 0 , x 1], [ x 1 , x 2], …, [ xi -1 , xi ], …, [ xn -1 , xn ]; длину i -го отрезка обозначим : 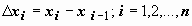; максимальную из длин отрезков обозначим 
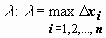. На каждом из отрезков [ xi -1 , xi ] выберем произвольную точку и составим сумму 
.
Сумма 
называется интегральной суммой.
Предел последовательности интегральных сумм при 
, не зависящий ни от способа разбиения отрезка [ a, b ] на части [ xi -1 , xi ], ни от выбора точек , называется определённым интегралом от функции f (x) по отрезку [ a, b ] и обозначается 
, где функция f (x) называется подынтегральной, числа a и b - соответственно, нижним и верхним пределами интегрирования.
.
Свойства определенного интеграла:
1. 
, если b=a.
2. 
.
3. 
.
4. Если y = f (x) интегрируема по отрезку [ a, b ] и точка c принадлежит этому отрезку, то 
.
5. Если и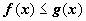 
, и функции f (x), g (x) интегрируемы по отрезку [ a, b ], то 
.
6. Если на отрезке [ a, b ] функция удовлетворяет неравенству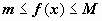 
, то 
.
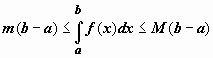7. Если функция f (x) интегрируема по отрезку [ a, b ], то 
.
8. ( Теорема о среднем ) Если f (x) непрерывна на отрезке [ a, b ], то существует точка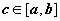 
, такая что 
.
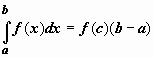Геометрический смысл определённого интеграла. Если f (x) >0 на отрезке [ a, b ], то 
равен площади криволинейной трапеции ABCD, ограниченной снизу отрезком [ a, b ], слева и справа - прямыми x = a и x = b, сверху – функцией y = f (x).
Формула Ньютона-Лейбница.
Если f (x) непрерывна на отрезке [ a, b ], и F (x) - некоторая первообразная функции 
, то 
.
