МОДУЛЬ 2. МАТЕМАТИЧЕСКИЙ АНАЛИЗ.
Тема 2.1. Теория пределов.
Основные понятия теории пределов.
Свойства пределов функций.
Замечательные пределы.
Правила вычисления пределов функций.
Пункт 1. Основные понятия теории пределов.
Число b называется пределом функции у = f(x) в точке а (или при х, стремящемся к а), если для всех значений х, достаточно близких к а и отличных от а, значения функции f(x) сколь угодно мало отличаются от числа b, т.е. выполняется условие |f(x) - b| <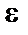 
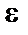, где - сколь угодно малое положительное число окрестности точки а, то есть 
.
Читают: Предел функции f(x) в точке а – число b, к которому стремятся значения функции f(x), когда х стремится к а или f(x) ® b при х ® а.
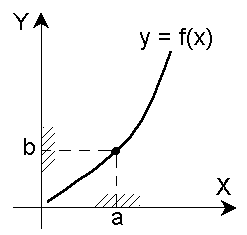
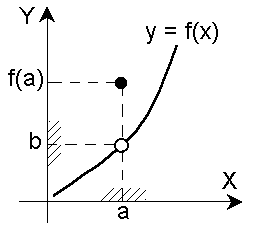
Окрестностью точки а называется любой интервал, содержащий точку внутри себя.
Число b называется пределом функции у = f(x) на бесконечности (или при х, стремящемся к бесконечности), если при всех достаточно больших по модулю значений аргумента х соответствующие значения функции f(x) сколь угодно мало отличаются от числа b.
Теорема о единственности предела. Если функция имеет предел при x→a, то этот предел единственный.
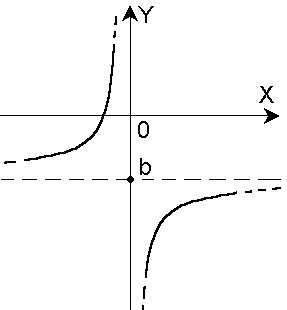
Пределом функции f(x) в точке хо слева (справа) называется предел, вычисляемый в предположении, что х стремится к хо, оставаясь все время меньше (больше) хо.
Пределы слева и справа называются односторонними пределами и соответственно обозначаются: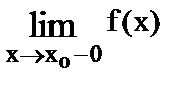 
и 
.
Величина f(x) называется бесконечно малой, если ее предел равен 0, то есть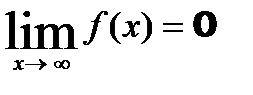 
.
Величина называется бесконечно большой, если ее предел равен ¥, то есть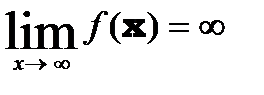 
.
Следует отметить, что обратная бесконечно малой величины является бесконечно большой величиной и наоборот.
Пункт 2. Свойства пределов функции.
Если существуют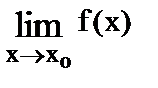 
и 
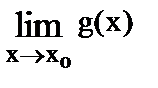, то
1. 
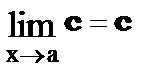где с = const
2. 
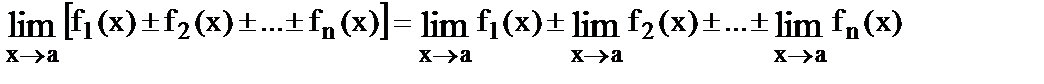
3. 
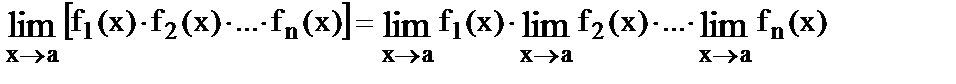
4. 
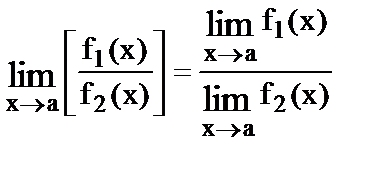где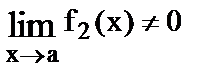 
5. 
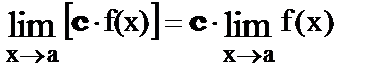где с = const
6. Если f1(x) £ f(x) £ f2(x) и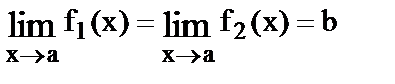 
, то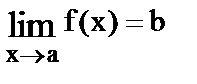 
7. 
8. 
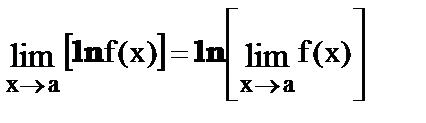
9. 
.
Пункт 3. Замечательные пределы.
Существует два замечательных предела, которые облегчают процесс вычисления различных пределов функций – это первый и второй замечательные пределы функций.
Первый замечательный предел функции.
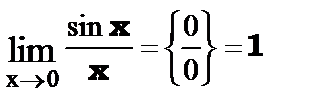или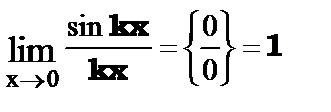 
.
Следствия из первого замечательного предела:
Можно использовать следствия этого предела:
; 
; 
; 
Примеры.
1. 
.
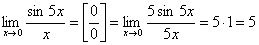2. 
.
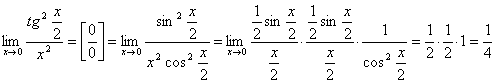3. 
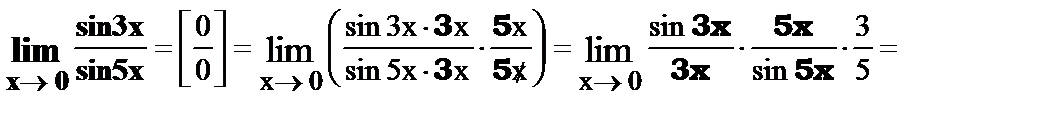
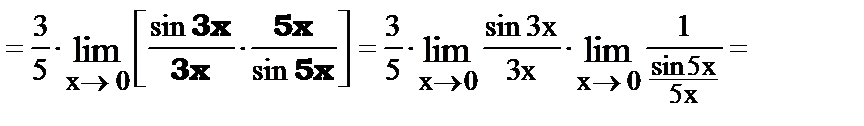
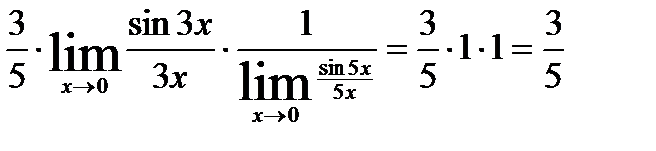
4. 
.
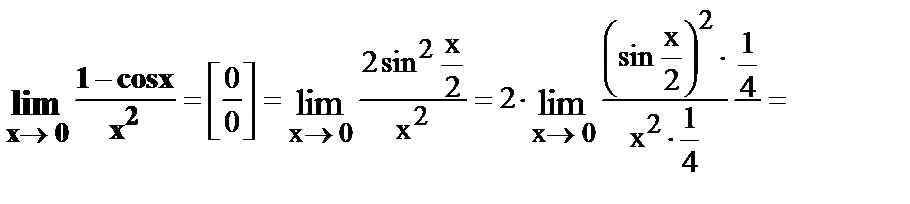
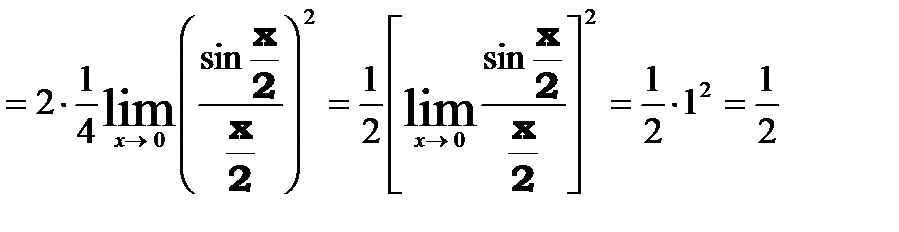Второй замечательный предел функции.
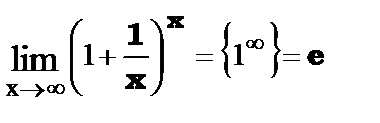или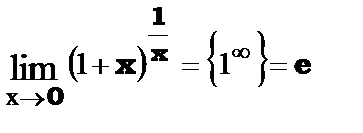 
, где число е - число Эйлера и е» 2,718281…
Примеры:
5. 
.
6. 
.
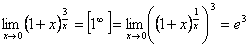7. 
.
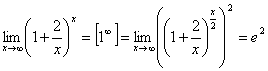8. 
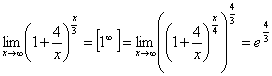
9. 
.
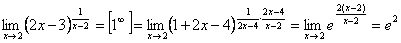10. 
Пункт 4. Правила вычисления пределов.
При вычислении пределов различных функций могут появиться неопределенные выражения вида: 
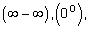
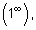
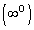. Такие выражения называются неопределенностями. Поэтому наша задача сводится к раскрытию таких неопределенностей.
Неопределенность вида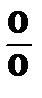 
.
Для того, чтобы раскрыть неопределенность подобного вида, необходимы тождественные преобразования (разложение на множители, применение формул сокращенного умножения и т.д.)
Примеры.
11. 
12. 
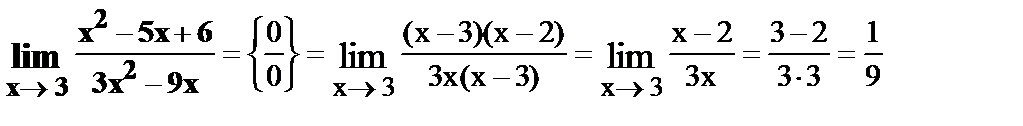
13. 
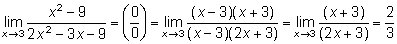
Иногда неопределенность такого вида появляется в пределах функций, содержащих знак радикала. В этом случае уничтожают иррациональность, для чего числитель и знаменатель умножают на выражение, сопряженное выражению, которое содержит иррациональность, при этом используют формулу (a – b) (a + b) = a2 – b2.
Примеры:
14. 
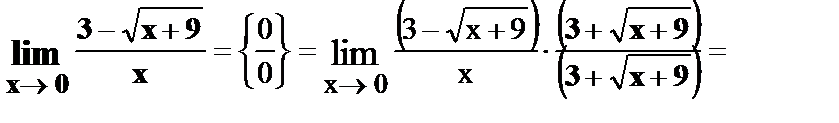
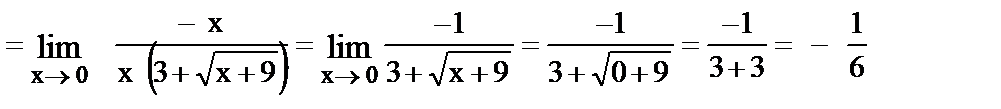
15. 
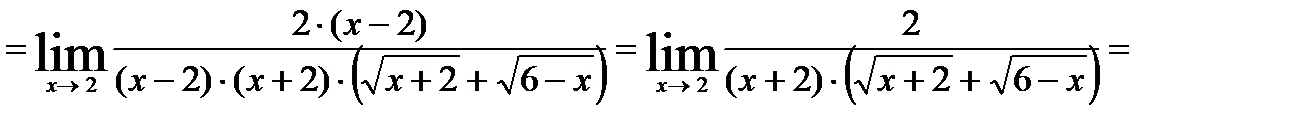
Неопределенность вида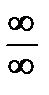 
.
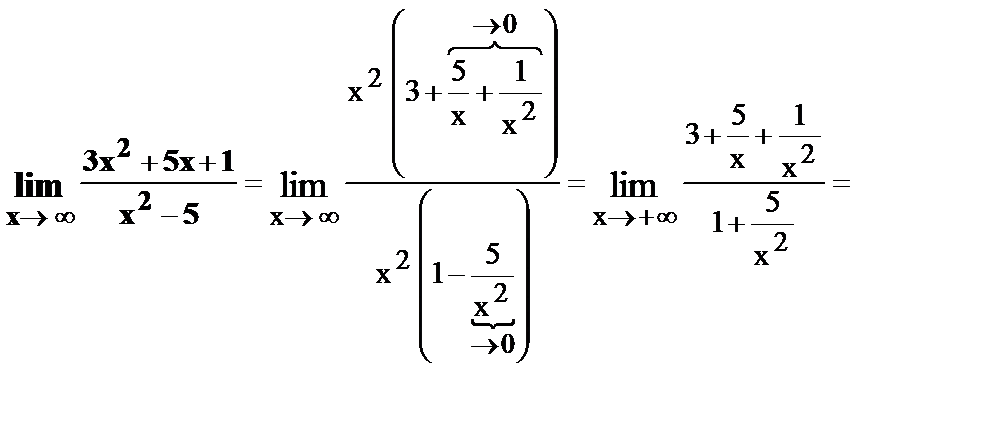
Для того, чтобы раскрыть неопределенность подобного вида, необходимо каждое слагаемой в числителе и знаменателе дроби разделить на наивысшую степень всей дроби.
Примеры:
16. 
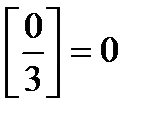
17. 
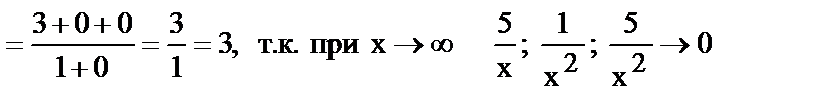
18. 
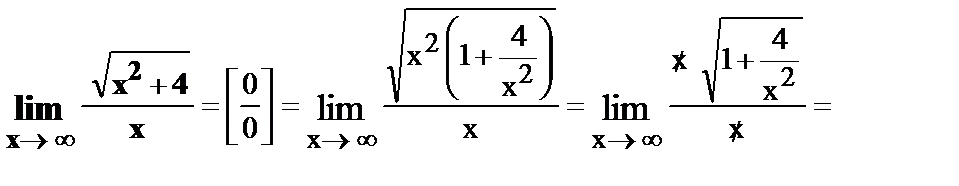
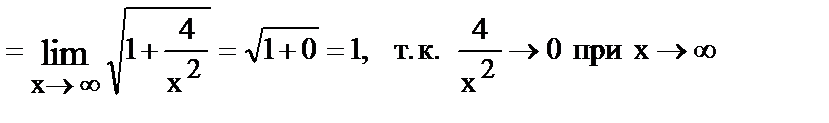
Неопределенность вида ¥ - ¥.
В этом случае нужно:
Ø выполнить вычитание дробей, сделать необходимые тождественные преобразования и свести к неопределенности вида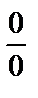 
или 
ИЛИ
Ø числитель и знаменатель одновременно умножить на сопряженное выражение и тем самым свести к неопределенности вида 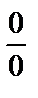или
ИЛИ
Ø преобразовать соответствующую разность f1(x) – f2(x) в произведение:
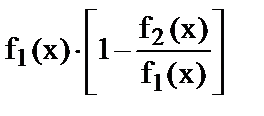и раскрыть неопределенность 
; 
, 
.
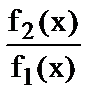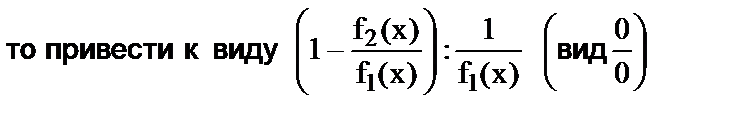Примеры:
19. 
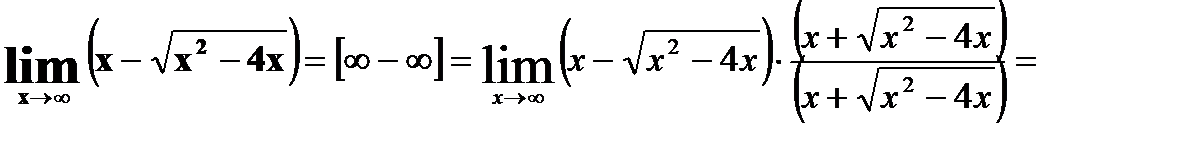
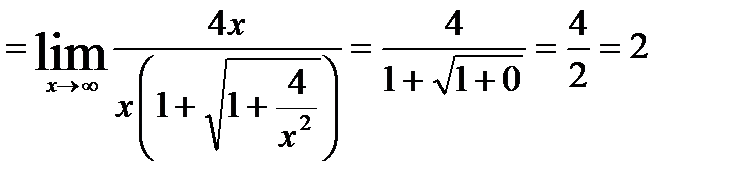
20. 
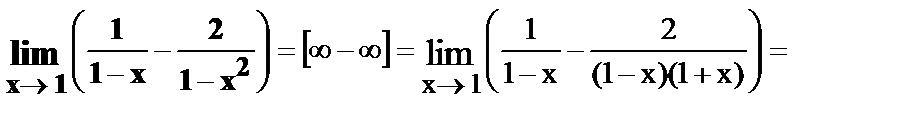
Неопределенность вида 0 × ¥.
Для раскрытия этой неопределенности необходимо преобразовать соответствующее произведение f1(x) × f2(x), где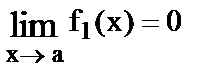 
и 
, в частное 
или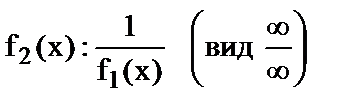 
.
Примеры:
21. 
.
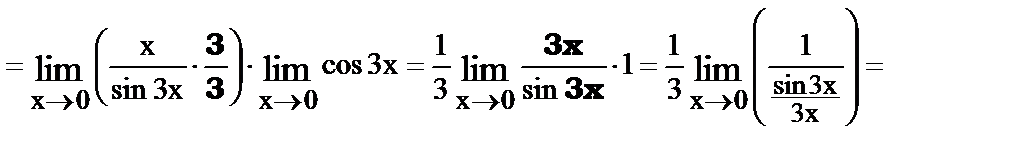
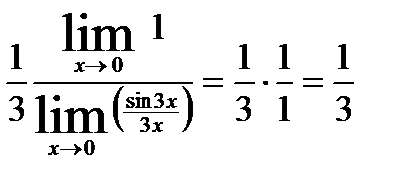22. 
.
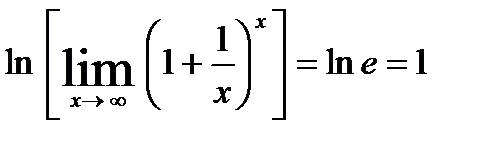Часто для вычисления пределов любых функций используют производные функций. Это носит название правила Лопиталя.
Первое правило Лопиталя.
Если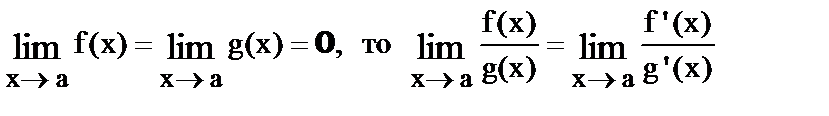 
.
Второе правило Лопиталя.
Если 
.
Примеры.
23. 
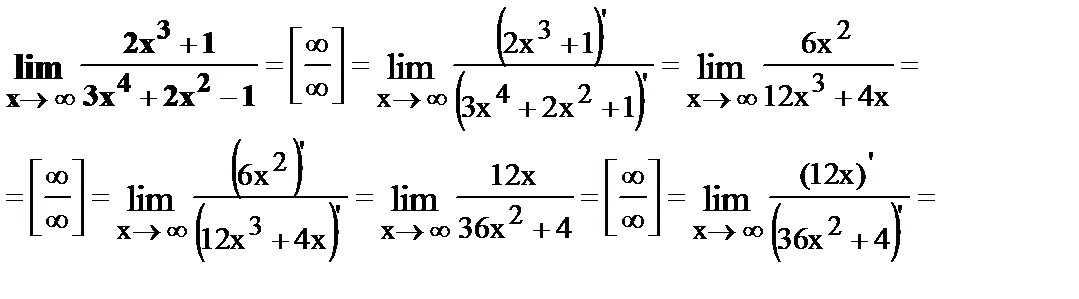
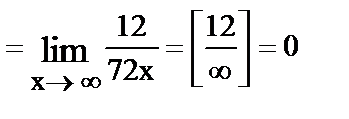
24. 
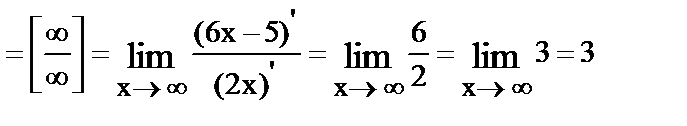
25. 
.
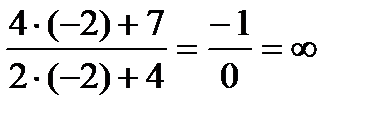26. 
.
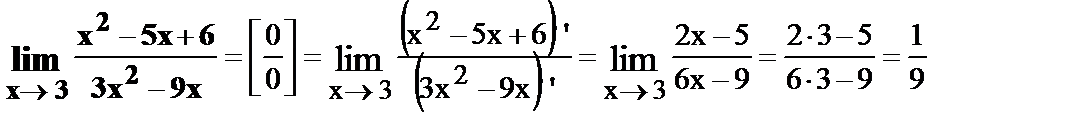