Для степенного ряда а0+а1+а2x2+…+аnxn+… возможны только три случая: 1) ряд сходится в единственной точке x=0; 2) ряд сходится для всех значений x; 3) существует такое R>0, что ряд сходится для всех значений x из интервала (-R, R) и расходится для всех значений x вне отрезка [-R,R]. Интервал (-R, R) называют интервалом сходимости ряда а0+а1+а2x2+…+аnxn+…, а число R – радиусом сходимости этого ряда. Если существует предел D= 
, отличный от нуля, то радиус сходимости степенного ряда а0+а1+а2x2+…+аnxn+… равен 
.
Интегрируемость и дифференцируемость суммы степенного ряда на интервале сходимости.
Пусть функция f(x) разлагается на интервале (-R, R) в степенной ряд f(x)= а0+а1+а2x2+…+аnxn+…. Рассмотрим степенной ряд а1+2а2x+…+nаnxn-1+…, полученный почленным дифференцированием ряда f(x)= а0+а1+а2x2+…+аnxn+…. Тогда: 1) ряд а1+2а2x+…+nаnxn-1+… имеет тот же радиус сходимости R, что и ряд f(x)= а0+а1+а2x2+…+аnxn+…; 2) на всем интервале (-R, R) функция f(x) имеет производную f`(x), которая разлагается в степенной ряд а1+2а2x+…+nаnxn-1+….
Если функция f(x) разлагается в степенной ряд на интервале (-R, R), то она интегрируема в этом интервале. Интервал от суммы ряда равен сумме интегралов от членов ряда.
Ряды Тейлора (Маклорена)
Пусть функция f(x) определена в некоторой окрестности точки x=0 и имеет в этой точке производные всех порядков. Степенной ряд 
называют рядом Маклорена для функции f(x).
Достаточное условие разложимости функции в ряд Маклорена
Пусть функция f(x) определена и бесконечно дифференцируема в интервале (-r, r). Если существует такая константа М, что во всех точках указанного интервала выполняются неравенства 
, то в этом интервале ряд Маклорена сходится к функции f(x).
Разложение в ряд Маклорена функций
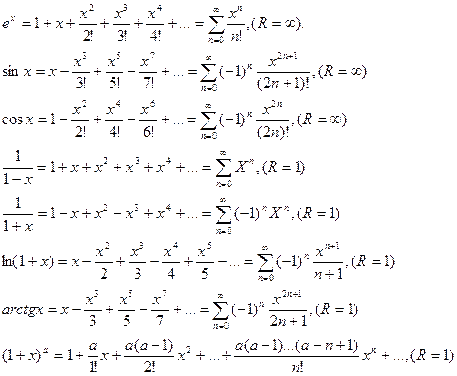
Теорема о существовании и единственности решения задачи
Коши для уравнения первого порядка в нормальной форме.
Если в некоторой окрестности точки 
функция f(x,y) определена, непрерывна и имеет непрерывную частную производную 
, то существует такая окрестность точки , в которой задачи Коши 
, 
имеет решение, притом единственное.
Если задача Коши , имеет единственное решение, то это решение называется частным решением уравнения .
Уравнения с разделяющимися переменными. Автономные
Уравнения.
Уравнения с разделяющимися переменными. Это дифференциальные уравнения вида: 
, где f(x) и g(x) – непрерывные функции. Запишем это уравнение в форме: 
. Для отыскивания решения этого уравнения необходимо, как говориться, разделить в нем переменные, т.е. переписать уравнение следующим образом: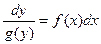 
в предположении, что в рассматриваемой области 
. Теперь левая часть уравнения содержит только переменную y, а правая – только x. Интегрируя обе части этого уравнения получим: 
. Таким образом, найден общий интеграл уравнения.
Частным случаем является автономное уравнение 
Его интегральные кривые при параллельном переносе вдоль оси абсцисс переходят друг в друга.
