Непрерывность функции нескольких переменных

Функция f(р), определенная на множестве Х из Rn, называется непрерывной в точке р0(принадлежащем Х), если Предел при р стрем к р0 от f(р) = f(р0). Или же если р0 – изолированная точка множ-ка Х.

Фf(р), определенная на множестве Х из Rn, называется непрерывной на этом множистве, если она непрерывна в каждой точке множ Х.

Любая элементарная ф непрерывна на всей области ее определения.

 

60.Свойства функций, непрерывных на замкнутом ограниченном множестве: ограниченность, достижение наибольшего и наименьшего значений.

1. Если числовая функция f отnпеременных задана на ограниченном и замкнутом множестве Х из Rn, то она ограничена на этом множестве.

2... то существует точка р0 принадлежащая Х, в которой f принимает свое наименьшее значение, и точка q0 принадлежащая Х, в которой fпринимает свое наибольшее значение.

 

61.Частные производные функции нескольких переменных.

Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения частного приращения функции к приращению соответствующей независимой переменной, когда это приращение стремится к нулю.

Частные производные функции z=f(x,y) в точке (x₀,y₀) обозначаются так:

z’x, dz/dx, f’x(x₀,y₀) – производная по x;

z’y, dz/dy, f’y(x₀,y₀) – производная по y.

 

62.Дифференцируемость функции нескольких переменных.

Пусть функция z=f(x, y) определена в некоторой области D на плоскости xOy. Возьмем точку (x, y) Î D и выбранным значениям x и y дадим любые приращения D x и D y, но такие, чтобы точка (x+ D x, y+ D y) Î D.

Определение. Функция z=f(x, y) называется дифференцируемой в точке (x, y) Î D, если полное приращение D x=f(x+ D x, y+ D y)-f(x,y) этой функции, отвечающее приращениям D x, D y аргументов, можно представить в виде D z=A D x+B D y+ a ( D x, D y) D x+ b ( D x, D y) D y, где A и B не зависят от D x и D y (но вообще зависят от x и y), а a ( D x, D y) и b ( D x, D y) стремятся к нулю при стремлении к нулю D x и D y.

 

63.Дифференциал функции нескольких переменных.

Если функция z=f(x, y) дифференцируема в точке (x, y), то часть A D x+B D y приращения функции, линейная относительно D x и D y, называется полным дифференциалом этой функции в точке (x, y) и обозначается символом dz: dz=A D x+ bD y (2)

Таким образом, D z=dz+ a×D x+ b×D y

 

64.Достаточное условие дифференцируемости функции нескольких переменных.

Как известно, необходимым и достаточным условием дифференцируемости функции y=f(x) одной переменной в точке x0 является существование конечной производной f/(x) в точке x0. В случае, когда функция зависит от нескольких переменных, дело обстоит значительно сложнее: необходимых и достаточных условий дифференцируемости нет уже для функции z=f(x, y) двух независимых переменных x, y; есть лишь отдельно необходимые условия и отдельно – достаточные. Эти достаточные условия дифференцируемости функций нескольких переменных выражаются следующей

теоремой. Теорема. Если функция z=f(x, y) имеет частные производные fx/ и fy/ в некоторой окрестности точки (x0, y0) и если эти производные непрерывны в самой точке (x0, y0), то функция z=f(x, y) дифференцируема в точке (x0, y0).

 

65.Непрерывность дифференцируемой функции.

 

66.Однородные функции.

Пусть D Ì – область в , содержащая вместе с каждой своей точкой (Х1,…,Хn) и все точки вида (tx1,…,txn) при t>0.

Ф-ия f(Х1,…,Хn) с такой областью определения D наз однородной степени a, если для любого t>0 выполняется рав-но: f(tx1,…,txn)= 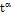f(Х1,…,Хn)

Однородный многочлен степени n явл однородной ф-ии той же степени однородности.

 

67. Формула Эйлера для однородной функции.

Например, формула Эйлера для ф-ии 3х переменных u=f(x,y,z) выглядит так:

(x,y,z)x+ 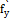(x,y,z)y+ (x,y,z)z=af(x,y,z)

68.Производная сложной функции.

Пусть f(x,y) – ф-я от 2 переменных х и у, а j(t) и y(t) – ф-ии от незав переменной t. В этом случае говорят что F(t)=f(j(t),y(t)) - сложная ф-я от t.

Если ф-я х=j(t), а у=y(t) дифференцируемы в точке t0, а ф-я z= f(x,y) дифференцируема в точке (j(t),y(t)), то сложная ф-я F(t)=f(j(t),y(t)) также дифференцируема в t0. При этом производная сложной ф-ии нах по формуле:

(t0)= (j(t0),y(t0)) j`(t0) + 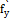(j(t0),y(t0)) y`(t0))

 

69.Производная по направлению.

Производной ф-ии f(x,y) в точке (x0,y0) по направлению e наз предел:

=

 

70.Градиент. Свойства градиента.

Градиентом ф-ии в точке М наз вектор, координаты которого равны соответствующим частным производным данной ф-ии в точке М. Для ф-ии 2х пер f(x,y) имеем:

Grad f(M)= ( (M), (M))

3х пер:

Grad f(M)= ( (M), (M), (M))

Свойства градиента

1. Производная в данной точке по направлению вектора имеет наибольшее значение, если направление вектора совпадает с направлением градиента. Это наибольшее значение производной равно .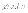

2. Производная по направлению вектора, перпендикулярного к вектору , равна нулю.

 

71) Частные производные высших порядков. Пусть задана функция f(x, y). Тогда каждая из ее частных производных(если они, конечно, существуют) 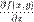и , которые называются также частными производными первого порядка, снова являются функцией независимых переменных x, y и может, следовательно также иметь частные производные. Частная производная 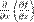обозначается через или , а через или . Таким образом, , и, аналогично, , . Производные и называются частными производными второго порядка. Определение: Частной производной второго порядка от функции z=f(x;y) дифференцируемой в области D,называется первая производная от соответствующей частной производной. Рассматривая частные производные от них, получим всевозможные частные производные третьего порядка: , , 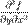и т. д.

 

72) Теорема о равенстве смешанных производных.

Смешанные частные производные одной и той же функции, отличающиеся лишь порядком дифференцирования, равны между собой при условии их непрерывности.

 

73) Формула Тейлора для функции нескольких переменных с остаточным членом в форме Лагранжа.

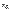Пусть при всех х принадлежит Е существует (n+1)-я производная . Тогда для любого х существует точка , лежащая между и х (то есть при ), такая что

 

74) Локальные экстремумы функций нескольких переменных.

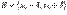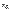Пусть функция определена в некоторой окрестности , , некоторой точки своей области определения. Точка называется точкой локального максимума, если в некоторой такой окрестности выполняется неравенство 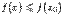(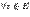), и точкой локального минимума, если . Понятия локальный максимум и локальный минимум объединяются термином локальный экстремум.

 

75) Необходимое условие локального экстремума функций нескольких переменных.

Если точка --это точка локального экстремума функции 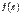, и существует производная в этой точке , то .

 

76) Достаточное условие локального экстремума функций нескольких переменных.

Обозначим Если D > 0, A > 0, то - точка минимума. Если D > 0, A < 0, то - точка максимума. Если D < 0, экстемума в точке нет. Если D = 0, необходимы дополнительные исследования.

 

77) Условный экстремум.

Условный экстремум- минимальное или максимальное значение, достигаемое данной функцией (или функционалом) при условии, что нек-рые другие функции (функционалы) принимают значения из заданного допустимого множества. Если условия, ограничивающие в указанном смысле область изменения независимых переменных (функций), отсутствуют, то говорят о безусловном экстремуме.

 

78) Метод Лагранжа

Пусть — точка условного экстремума функции при выполнении уравнений связи. Тогда в этой точке градиенты являются линейно зависимыми, то есть но .

 

79) Наибольшее и наименьшее значение непрерывной функции на замкнутом ограниченном множестве.

Пусть функция z = f(х;у) определена и непрерывна в ограниченной замкнутой области. Тогда она достигает в некоторых точках своего наибольшего М и наименьшего m значений (т.н. глобальный экстремум). Эти значения достигаются функцией в точках, расположенных внутри области, или в точках, лежащих на границе области.

 

80) Кратные интегралы и их свойства. Условия интегрируемости функции.

В математическом анализе кратным или многократным интегралом называют множество интегралов, взятых от переменных. Свойства: Линейность по функции. Пусть измеримо, функции и интегрируемы на , тогда . Аддитивность по множеству интегрирования. Пусть множества и измеримы, и . Пусть также функция определена и интегрируема на каждом из множеств 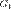и . Тогда интеграл по существует и равен . Монотонность по функции. Пусть измеримо, функции и интегрируемы на , причем . Тогда . Интегральное неравенство треугольника. Следствие предыдущего свойства. Интегральная теорема о среднем. 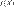Пусть - компакт, функция непрерывна и интегрируема на , тогда Постоянная функция интегрируема на любом измеримом множестве , причем . Как следствие, .

Условия: 1) Необходимое условие интегрируемости. Если функция интегрируема на отрезке, то она ограничена на нем. 2) Необходимое и достаточное условие интегрируемости. Для того, чтобы ограниченная на некотором отрезке функция была интегрируема на нем необходимо и достаточно, чтобы lim∣τ∣→0(Sτ−sτ)=0. 3) Интегрируемость непрерывной функции. Если f(x) непрерывна на [a,b]f(x)∈C[a,b], то она интегрируема на нем. Функция определенная и монотонная на [a,b] интегрируема на нем. Если функция ограничена и непрерывна на отрезке, кроме, может быть, конечного числа точек, то она интегрируема на нем.