Последовательность частичных сумм. Сумма ряда. Сходящиеся ряды

Пусть дана некоторая последовательность действительных чисел а_п. Тогда сумма бесконечного числа членов этой последовательности

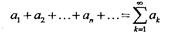
называется числовым рядом, а число а_п (n = 1,2,...) — членом ряда. Если член ряда а_п представлен в виде функции, натурального аргумента а_п= f (п), то его называют общим членом ряда. При этом сумму S_n = а₁ + а₂ +...+ а_п первых п членов ряда называют его n-ой частичной суммой. Таким образом, мы можем образовать новую последователь­ность - последовательность частичных сумм S₁=a₁, S₂=a₁+a₂, S₃=a₁+a₂+a₃, S_n =a₁+ a₂ +...+ a_n. Если эта последовательность имеет конечный предел S = lim S_n при n->infimity, то числовой ряд называется сходящимся, а число S — суммой ряда. В противном случае ряд называ­ют расходящимся.

Свойства сходящихся рядов.

1. Если ряд (l) сходится, то сходится и любой ряд, полученный из него отбрасыванием конечного числа членов. Ряд полученный отбрасыванием первых п членов суммы (l), называется п-м остатком ряда. Таким образом, ряд (l) и любой его остаток сходятся или расходятся одновременно.

2. Если каждый член сходящегося ряда (l), сумма которого равна
S, умножить на некоторое число k, то полученный ряд

также сходится, и его сумма равна kS.

3. Если даны два сходящихся ряда

и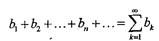

 

с суммами S и Т соответственно, то новый ряд полученный почленным сложением исходных рядов, также сходится, и его сумма равна S + T.

 

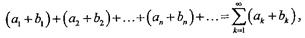
4. Если ряд (1) сходится, то сходится и любой ряд, полученный из него группировкой слагаемых, и суммы рядов одинаковы.

 

Необходимое условие сходимости числового ряда.

Теорема 5.1 (необходимый признак сходимости). Если ряд сходится, то предел его общего члена равен нулю.

Эквивалентная формулировка: Если предел общего члена ряда не равен нулю.или не сугцествует, то данный ряд расходится.

Доказательство. Пусть данный ряд сходится и его сумма равна S. Для любого натурального п имеем S_n= S_n-₁ + а_п или

A_n=S_n-S_n-1

При п -> infinity обе частичные суммы S_n и S_n-1 стремятся к пределу S, поэтому из равенства следует, что

Подчеркнем еще раз, что мы установили только необходимое условие сходимости ряда, т.е. усдовие, при нарушении которого ряд не может сходиться. С помощью этого признака можно дока­зывать только расходимость ряда.

Числовые ряды с неотрицательными членами.

Числовой ряд называется рядом с положительными членами, если общий член ряда а_п >0 для любого n=1,2,.... Критерием сходимости для таких рядов служит ограниченность последовательности частичных сумм ряда.

При решении задач на сходимость рядов первым шагом является проверка выполнения необходимого условия сходимости, т.е.