П р и м е р 1.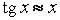 
, 
, потому что
.
П р и м е р 2.
.
О п р е д е л е н и е. Если для функции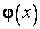 
можно подобрать числа 
и 
, где 
, такие, что
,
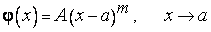то говорят, что функция 
есть главный степенной член функции 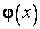в окрестности точки 
.
Правые части соотношений (3) – (7) суть, очевидно, главные степенные члены левых частей при .
Будем говорить, что 
на множестве 
имеет порядок 
или еще есть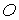 
- большое от на и при этом будем писать
на , (14)
если
,
где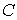 
- не зависящая от 
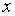положительная константа.
В частности, равенство
на
обозначает тот факт, что ограничена на .
П р и м е р ы:
1) 
на 
;
2) 
на 
;
3) 
на 
.
Производная функции. Задачи, приводящие к понятию производной (задача о мгновенной скорости, задача об угле наклона касательной к кривой).
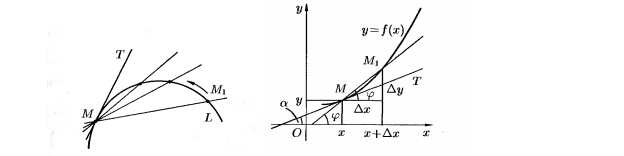
Основные правила дифференцирования. Таблица производных элементарных функций.
Производной от функции 
называется конечный предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
, или 
.
Геометрически производная представляет собой угловой коэффициент касательной к графику функции в точке х, то есть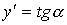 
.
Производная есть скорость изменения функции в точке х.
Отыскание производной называется дифференцированием функции.
Основные правила дифференцирования
Пусть 
, тогда:
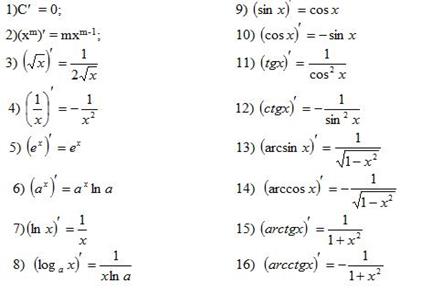
Дифференцирование неявных функций
Дифференцирование функций, заданных параметрически
Дифференцирование функций, заданных параметрически
Пусть функция задана параметрическими уравнениями 
,
тогда 
, или 
Приме: 
12. Дифференциал функции. Приближённые вычисления с помощью дифференциала.
I. Дифференциал функции.
Опр. Дифференциал функции называется главная линейная относительно 
часть приращения функции, равная произведению производной на приращение независимой переменной 
.
1. Понятие дифференциала:
Пусть функция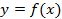 
, определена на промежутке Х и дифференцируема в некоторой окрестности точки 
. Тогда существует конечная производная 
=f’(x).
На основании теоремы о связи бесконечно малых величин с пределами ф-ций можно записать
Где 
-бесконечно малая величина при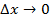 
, откуда 
.
Таким образом, приращение ф-ции 
состоит из двух слагаемых: 1)линейного относительно 
;2) нелинейного (представляющего бесконечно малую более высокого прядка, чем , ибо 
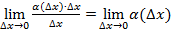=0).
Орп. Дифференциалом ф-ции называется главная, линейная относительно часть приращения ф-ции, равная произведению производной на приращение независимой переменной 
.
Дифференциал ф-ции независимой переменой равен приращению этой переменной. Т.к.
Прим. Найти диффрнц. ф-ции 
. Решение: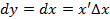 
, откуда 
.
Поэтому формулу для дифференцирования ф-ции можно записать в виде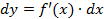 
, откуда 
еперь мы видим, что 
не просто символическое обозначение производной, а обычная дробь с числителем 
и знаменателем 
.
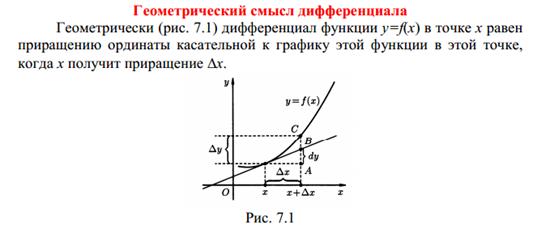
Т.е. геометрический смысл дифференцируемости f (x) в точке х
0 состоит в том, что расстояние от точки на ее графике до соответствующей
на касательной стремится к нулю "быстрее", чем ∆х.
Свойства дифференциала.
С-ва дифференц, фактически аналогичны свойствам производной, одним из отличительных свойств явл. с-во инвариантности форм дифференциала(6).
