Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию | x – a | < δ, x ≠ a, выполняется неравенство | f (x) – A | < ε.
Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности  такой, что
такой, что  сходящейся к числу a, соответствующая последовательность значений функции
сходящейся к числу a, соответствующая последовательность значений функции  сходится к числу A.
сходится к числу A.
Если функция f (x) имеет предел в точке a, то этот предел единственный.
Число A 1 называется пределом функции f (x) слева в точке a, если для каждого ε > 0 существует δ > 0 такое, что для всех  выполняется неравенство
выполняется неравенство 
Число A 2 называется пределом функции f (x) справа в точке a, если для каждого ε > 0 существует δ > 0 такое, что для всех  выполняется неравенство
выполняется неравенство 
Предел слева обозначается  предел справа –
предел справа –  Эти пределы характеризуют поведение функции слева и справа от точки a. Их часто называют односторонними пределами. В обозначении односторонних пределов при x → 0 обычно опускают первый нуль:
Эти пределы характеризуют поведение функции слева и справа от точки a. Их часто называют односторонними пределами. В обозначении односторонних пределов при x → 0 обычно опускают первый нуль:  и
и  . Так, для функции
. Так, для функции 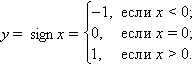


Если для каждого ε > 0 существует такая δ-окрестность точки a, что для всех x, удовлетворяющих условию | x – a | < δ, x ≠ a, выполняется неравенство | f (x)| > ε, то говорят, что функция f (x) имеет в точке a бесконечный предел:

|
Так, функция 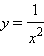 имеет в точке x = 0 бесконечный предел
имеет в точке x = 0 бесконечный предел  Часто различают пределы, равные +∞ и –∞. Так,
Часто различают пределы, равные +∞ и –∞. Так, 

Если для каждого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство | f (x) – A | < ε, то говорят, что предел функции f (x) при x, стремящемся к плюс бесконечности, равен A:

|
Аналогично формулируется определение предела при x, стремящемся к минус бесконечности: 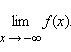 В качестве примера приведем функцию
В качестве примера приведем функцию  которая стремится на бесконечности к нулю:
которая стремится на бесконечности к нулю: 
Наконец, запись 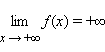 означает, что для любого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство f (x) > ε. Запись
означает, что для любого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство f (x) > ε. Запись  означает, что для любого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство f (x) < –ε. Запись
означает, что для любого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство f (x) < –ε. Запись  означает, что для любого ε > 0 существует такое δ > 0, что для любого x < –δ выполняется неравенство f (x) < –ε.
означает, что для любого ε > 0 существует такое δ > 0, что для любого x < –δ выполняется неравенство f (x) < –ε.
Если функция f (x) имеет конечный предел в точке a, то существует окрестность точки a, в которой функция f ограничена (возможно, что в самой точке a функция не определена). При этом, если A ≠ 0, то найдется окрестность точки a, в которой (быть может, за исключением самой точки a) значения функции f имеют тот же знак, что и число A.
Если существует такое δ > 0, что для всех x, принадлежащих δ-окрестности точки a, выполняются неравенства
| g (x) ≤ f (x) ≤ h (x), |
и если
 , ,
|
то существует 
Если существует такое δ > 0, что для всех x, принадлежащих δ-окрестности точки a, справедливо неравенство
| f (x) < g (x), |
и если 
 то A ≤ B.
то A ≤ B.
Если функции f (x) и g (x) имеют конечные пределы в точке a, причем 
 то
то
·  ,
,
· 
·  если B ≠ 0 и если g (x) ≠ 0 в δ-окрестности точки a.
если B ≠ 0 и если g (x) ≠ 0 в δ-окрестности точки a.
Из существования пределов f (x) в точке a и g (y) в точке f (a) следует существование предела сложной функции g (f (x)) в точке a.
Для вычисления пределов часто используют так называемые замечательные пределы:
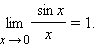 
|
Доказательство
Другие важные пределы (при a > 0, a ≠ 1):
|
следуют из замечательных пределов и свойства предела обратной функции.
Функция α (x) называется бесконечно малой при x → a (здесь a – конечное число или ∞), если  Функция x = 0 является бесконечно малой функцией в каждой точке. Примерами бесконечно малых (на бесконечности) функций являются зависимость силы тяжести от расстояния до притягивающего центра или зависимость скорости движения по параболической орбите от времени.
Функция x = 0 является бесконечно малой функцией в каждой точке. Примерами бесконечно малых (на бесконечности) функций являются зависимость силы тяжести от расстояния до притягивающего центра или зависимость скорости движения по параболической орбите от времени.
· Сумма конечного числа бесконечно малых при x → a функций есть бесконечно малая функция.
· Произведение бесконечно малой при x → a функции на ограниченную в некоторой окрестности точки a функцию есть бесконечно малая при x → a функция.
Если в некоторой окрестности a определены функции f (x), g (x), h (x) такие, что f (x) = g (x) h (x),  , то функции f (x) и g (x) называются эквивалентными при x → a:
, то функции f (x) и g (x) называются эквивалентными при x → a:
| f (x) ~ g (x). |
Так, функции  и
и 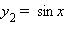 эквивалентны при x → 0, так как
эквивалентны при x → 0, так как  а второй множитель стремится к 1 при x → 0. Другие примеры эквивалентных функций при x → 0:
а второй множитель стремится к 1 при x → 0. Другие примеры эквивалентных функций при x → 0:
| sin x ~ x tg x ~ x arcsin x ~ x arctg x ~ x ex – 1 ~ x ln (1 + x) ~ x (1 + x)α – 1 ~ α x. |
При вычислении пределов функций можно использовать понятие эквивалентности.
Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела.
Следствие. Если две функции f (x) и g (x) равны в некоторой окрестности точки  , за исключением, может быть, самой точки
, за исключением, может быть, самой точки  , то либо они имеют один и тот же предел при
, то либо они имеют один и тот же предел при  , либо обе не имеют предела в этой точке.
, либо обе не имеют предела в этой точке.
Теорема 2. Если функции f(x) и g(x) имеют пределы в точке  , то:
, то:
1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
 (2)
(2)
2) предел произведения функций равен произведению пределов сомножителей, т.е.


 (3)
(3)
3) предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.
 (4)
(4)
Замечание. Формулы (2) и (3) справедливы для любого конечного числа функций.
Следствие 1. Предел постоянной равен самой постоянной, т.е.

Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.

Теорема 3 (о пределе сложной функции). Если существует конечный предел

а функция f(u) непрерывна в точке  , то
, то
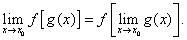
Другими словами, для непрерывных функций символы предела и функции можно поменять местами.
Предел функции в бесконечно удалённой точке
Аналогично пределу последовательности определяется предел функции при  .
.
Число a называется пределом функции f (x) в бесконечно удалённой точке

если для произвольно малого положительного числа  можно найти такое число N, что для всех
можно найти такое число N, что для всех

выполняется неравенство
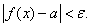
Свойства пределов функции
1) Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:

2) Предел суммы
Предел суммы двух функций равен сумме пределов этих функций:

Аналогично предел разности двух функций равен разности пределов этих функций.
3) Предел произведения функции на постоянную величину
Постоянный коэффициэнт можно выносить за знак предела:

4) Предел произведения
Предел произведения двух функций равен произведению пределов этих функций:

5) Предел частного
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:









