1. Вибір бажаної типової ДЧХ.
Для спрощення вибору ДЧХ існує набір розрахованих і побудованих перехідних функцій систем, які відповідають різноманітним типовим ДЧХ із різними параметрами. Якщо, наприклад, взяти систему з найбільш простою, а саме із прямокутною трапецієподібною ДЧХ, що має коефіцієнт нахилу 
, то ми одержимо гарні перехідні процеси, які можуть бути прийняті за оптимальні.
Звичайно, у реальних системах реалізувати ДЧХ у вигляді простої трапеції (рис. 1,а) досить складно. У цьому випадку або необхідно складний коригувальний пристрій, або зовсім неможливо реалізувати на практиці такі характеристики.
| P(w) |
| 0,5 |
| wа |
| w |
| Р(0) |
| Рmax |
| Pmin |
| P(w) |
| wП |
| wС |
| wП |
| w3 |
| w2 |
| w1 |
| w4 |
| w5 |
| w |
| w0 |
Рисунок 1. Типові ДЧХ
Значно простіше реалізувати типову ДЧХ, що зображена на рис.1,б і яка характеризується наступними параметрами:
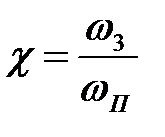– основний коефіцієнт нахилу;
– перший додатковий коефіцієнт нахилу;
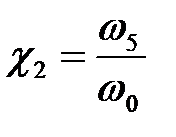– другий додатковий коефіцієнт нахилу;
– перший коефіцієнт форми;
– другий коефіцієнт форми.
Для різних значень коефіцієнтів 
, 
і 
встановлено, що найкращі перехідні процеси можуть бути отримані в системах із ДЧХ, що характеризується коефіцієнтами 
, 
, 
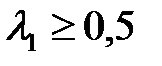. Величина перерегулювання при таких коефіцієнтах як правило залежить від Рmax > 0.
2. Визначення P max і P min типової ДЧХ.
Pmax і Pmin типової ДЧХ побічно характеризують перерегулювання в системі керування. Для визначення Pmax використовується номограма проф. В.В.Солодовникова (мал.2), що представлена у вигляді залежностей 
і 
.
Рисунок 2. Номограма для визначення Рmax і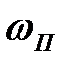 
.
Якщо ДЧХ має негативний «хвіст», то додатково викликане нею перерегулювання 
визначається за формулою:
.
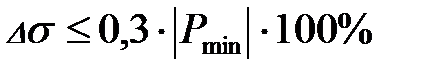Тоді величину максимального перерегулювання знайдемо з умови:
,
де величина 
визначається із графіка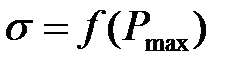 
(рис.2).
Загальне перерегулювання буде дорівнювати:
. (1)
На практиці приймають:
(2)
Таким чином, маючи графік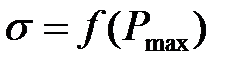 
і з огляду на (1) і (2), можна визначити Рмах і Рmin, які задовольняють заданому перерегулюванню 
.
3. Визначення частоти позитивності 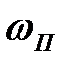типової ДЧХ.
Частота позитивності 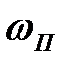типової ДЧХ побічно характеризують швидкодію системи керування. Визначається частота позитивності за графіком 
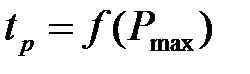номограми проф. В.В.Солодовникова виходячи із заданого часу регулювання 
й отриманого значення Pmax:
, 
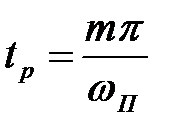де коефіцієнт 
знаходять із графіку 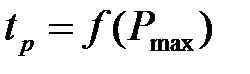(мал.2).
4. Визначення параметрів бажаної ЛАЧХ.
- вибір частоти зрізу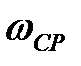 
бажаної ЛАЧХ:
- вибір нахилу бажаної ЛАЧХ в області середніх частот (частоти зрізу). Нахил асимптоти бажаної ЛАЧХ, що проходить через частоту зрізу приймають рівним – 20 дБ/дек. При більшому нахилі важко забезпечити необхідний запас стійкості, перерегулювання й коливальність у системі.
- визначення ширини середньочастотної ділянки бажаної ЛАЧХ.
Для задоволення заданого значення перерегулювання необхідно виконати наступні умови:
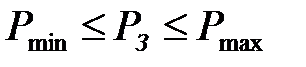(3)
Еквівалентні вимоги до ЛАЧХ можна знайти за допомогою номограми перекладу ЛАФЧХ розімкнутої системи у ДЧХ замкнутій (рис.3). З номограми видно, що умова (3) еквівалентна тому, щоб ЛАФЧХ не заходила в заборонну область, обмежену кривими з індексами Рмах і Рmіn (приблизно ці криві можна замінити прямокутником).
Рисунок 3. Визначення запасів стійкості по фазі й по амплітуді
З вимог до ЛАФЧХ випливають еквівалентні вимоги до ЛАЧХ і ЛФЧХ: для забезпечення заданого перерегулювання необхідно, щоб у діапазоні частот від 
до 
виконувалися наступні умови: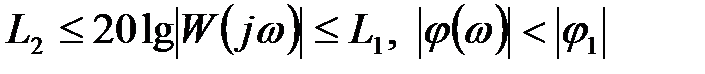 
.
Ординати L1 і L2, що знайдені з умов забезпечення заданого перерегулювання , називають запасом стійкості по амплітуді. Різниця D j(w)= 180 -|j1| називається запасом стійкості по фазі.
5. Побудова бажаної ЛАЧХ.
Бажана ЛАЧХ складається із трьох основних асимптот: низькочастотної, середньочастотної і високочастотної. Крім того, можуть бути асимптоти, що сполучають, з'єднуючі основні.
Низькочастотна ділянка бажаної ЛАЧХ відповідає за точність системи в сталому режимі. Вихідними даними для побудови цієї асимптоти є: необхідний порядок астатизму, величина помилки, вид вихідної ЛАЧХ. В області НЧ бажана ЛАЧХ - це пряма, що проходить через точку 
при 
. 
- розрахований з умови точності коефіцієнт передачі розімкнутого контуру:
- для системи з астатизмом першого порядку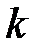 
визначається з умови одержання заданої швидкісної помилки 
при відомій величині вхідного впливу 
. Загальний коефіцієнт підсилення системи з астатизмом першого порядку дорівнює:
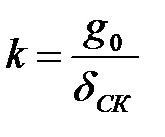
- для статичної системи загальний коефіцієнт підсилення системи визначається за формулою:
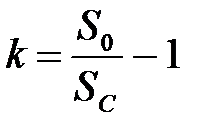
де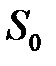 
– статизм об'єкта; 
– статизм системи;
- Якщо задано максимально припустиму амплітуду сигналу помилки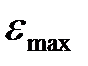 
при гармонійному вхідному впливі 
, те низькочастотна частина бажаної ЛАЧХ повинна розташовуватися не нижче контрольної точки, що має на частоті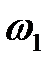 
ординату 
(точка F).
- Якщо вхідний вплив має більш складний вид, чим гармонійний вплив і відомі максимальні значення його першої й другої похідних, то можна підібрати еквівалентний гармонійний вплив з такими ж значеннями похідних. З умови рівності максимальних значень похідних реального вхідного впливу й еквівалентного гармонійного обчислюють еквівалентні значення частоти й амплітуди:
; 
.
Проведення бажаної ЛАЧХ на 3 дБ вище точки з координатами 
(точка F) забезпечує динамічну помилку не більше заданої.
На практиці за низькочастотну асимптоту бажаної ЛАЧХ приймають НЧ асимптоту вихідної ЛАЧХ із необхідним коефіцієнтом передачі.
Середньочастотна асимптота бажаної ЛАЧХ і її сполучення з низькочастотної визначають динамічні властивості системи – стійкість і показники якості перехідної характеристики.
Середньочастотна асимптота бажаної ЛАЧХ проводиться через точку 
з нахилом - 20 дБ/дек. При більшому нахилі важко забезпечити необхідний запас стійкості й припустиме перерегулювання.
Довжина середньочастотної асимптоти встановлюється виходячи з необхідного запасу стійкості (використовуючи знайдені раніше значення L1 і L2). Із цих же міркувань вибирають її сполучення з низькочастотної асимптотою. Крім того, асимптоту, що сполучає, варто вибирати так, щоб характеристика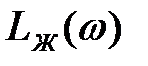 
можливо менше відрізнялася від 
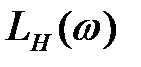і коригувальний пристрій було можливо більше простим.
Спочатку потрібно провести прямі з ординатами L1 і L2, до перетинання з якими продовжують середньочастотну асимптоту. Потім із крапки перетинання середньочастотної асимптоти із прямою L1 нанести асимптоту, що сполучає, з нахилом -40 дБ/дек або -60 дБ/дек до перетинання з низькочастотною асимптотою.
При сполученні необхідно забезпечити, щоб в інтервалі частот від 
до в якому значення ординати бажаної ЛАЧХ укладені між L1 і 0, запас стійкості по фазі був не менше D j(w)= 180 -|j1|. Якщо ж запас стійкості по фазі менше необхідного, то асимптоту, що сполучає, необхідно перемістити вліво. У іншому випадку (при занадто великому запасі стійкості) асимптота, що сполучає, переміщається вправо. Чим більший діапазон займає низькочастотна асимптота, тим краще система відтворює низькочастотні зміни впливу, що задає.
Високочастотна асимптота бажаної ЛАЧХ мало впливає на властивості системи. Тому її варто вибирати так, щоб коригувальний пристрій був як можливо більше простим. Це досягається при сполученні високочастотних асимптот характеристик 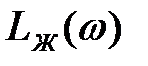і 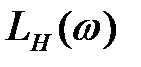. Якщо сполучення не вдається, то високочастотна асимптот 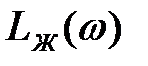повинна мати той же нахил, що й високочастотна асимптот .
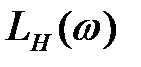Після побудови бажаної ЛАЧХ визначають характеристику коригувального пристрою.
ЛАЧХ послідовного коригувального пристрою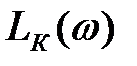 
визначаю графічним вирахуванням ординат ЛАЧХ вихідної (некоректованої) системи з ординат бажаної ЛАЧХ:
.
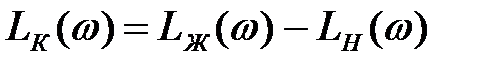За отриманим вираженням 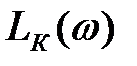знаходять передатну функцію послідовного коригувального пристрою Wк1(p). Потім з'ясовують, при якому значенні передатної функції Wк2(p) паралельного коригувального пристрою й при якому значенні передатної функції Wк3(p) прямого паралельного коригувального пристрою буде отриманий той же ефект. Потім уже можна вирішувати, який коригувальний пристрій доцільніше створювати.
Після вибору технічної реалізації обраного типу коригувального пристрою визначають показники якості в скоректованій замкнутій системі управління.
ПЕРЕЛІК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ
1. Теория автоматического управления / Под ред. А.А.Воронова - М.: Высшая школа, 1986, ч. 1, 2.
2. Теория автоматического управления / Под ред. А.В.Нетушила - М.: Высшая школа, 1983. – 432 с.
3. Попов Е.П. Теория линейных систем автоматического регулирования и управления. М.: Наука, 1989. 304 с.
4. Зайцев Г.Ф., Стеклов В.К., Бріцький О.І. Теорія автоматичного управління. - К., Техніка, 2002.- 688 с.
5. Попович М.Г., Ковальчук О.В. Теорія автоматичного керування. Підручник. – Київ: Либідь, 1997. – 544с.
6. Лукас В. А. Теория автоматического управления. – М.: Недра, 1990. – 416 с.
7. Зайцев Г.Ф. Теория автоматического управления и регулирования. Киев: Вища школа, 1988 - 431 с.
Навчальне видання
Конспект лекцій з курсу
"Теорія автоматичного управління"
Частина 1 - Аналіз та синтез лінійних САУ
Для студентів, що навчаються за напрямом
6.050201“Системна інженерія” (СУА)
(для денної й заочної форм навчання)
Укладач: Федюн Роман Валерійович, к.т.н, доц.
Рецензент Секірін Олександр Іванович, к.т.н, доц.
Відповідальний
за випуск Бессараб Володимир Іванович, к.т.н., доц.., зав. каф.
