В некоторых задачах используется понятие "плавучесть", означающее разность между подъемной силой Архимеда и силой тяжести. Звездочкой помечены задачи повышенной сложности (варианты 158-167).
Задача 114. Ведерко с водой, привязанное к веревке длиной 60 см, равномерно вращается в вертикальной плоскости. Найти: 1) наименьшую скорость вращения ведерка, при которой в высшей точке вода из него не выливается, 2) натяжение веревки при этой скорости в высшей и низшей точках окружности. Масса ведерка с водой 2 кг.
Задача 115. Камень, привязанный к веревке, равномерно вращается в вертикальной плоскости. Найти массу камня, если известно, что разность между максимальным и минимальным натяжениями веревки равна 9,8 Н.
Задача 116. Гирька массой 50 г, привязанная к нити длиною в 25 см, описывает в горизонтальной плоскости окружность. Скорость вращения гирьки соответствует 2 об/с. Найти натяжение нити.
Задача 117. Диск вращается вокруг вертикальной оси, делая 30 об/мин. На расстоянии 20 см от оси вращения на диске лежит тело. Каков должен быть коэффициент трения между телом и диском, чтобы тело не скатилось с диска?
Задача 118. Определить скорость движения автомобиля массой 2 т по вогнутому мосту радиусом 100 м, если он давит на середину моста с силой 25 кН.
Задача 119. Самолет, летящий со скоростью 900 км/ч, делает “мертвую петлю”. Каков должен быть радиус “мертвой петли”, чтобы наибольшая сила, прижимающая летчика к сидению, была равна: пятикратному весу летчика? 2) десятикратному весу летчика?
Задача 120. Средняя высота спутника над поверхностью Земли 1700 км. Определить его скорость и период вращения.
Задача 121. Найти силу тяготения, действующую со стороны Земли на тело массой 1 кг, находящееся на поверхности Луны. Расстояние между центрами Земли и Луны принять равными 384 000 км.
Задача 122. Спутник делает 16 оборотов за время одного оборота Земли. Определить период, высоту и скорость спутника, считая его орбиту круговой.
Задача 123. Трамвайный вагон массой 5 тонн идет по закруглению радиусом 128 м. Найти силу бокового давления колес на рельсы при скорости движения 9 км/ч.
Задача 124. Гирька, привязанная к нити длиною 30 см, описывает в горизонтальной плоскости окружность радиусом 15 см. Какому числу оборотов в минуту соответствует скорость вращения гирьки? (59 об/мин)
Задача 125. Шарик на веревке длиной 50 см равномерно вращается в вертикальной плоскости. Найти, при какой частоте вращения веревка оборвется, если предел прочности веревки mg, где m - масса шарика.
Задача 126. Мотоциклист едет по горизонтальной дороге со скоростью 72 км/ч, делая поворот радиусом кривизны в 100 м. Насколько при этом он должен накрениться, чтобы не упасть при повороте?
Задача 127. Шоссе имеет вираж с уклоном в 10° при радиусе закругления дороги в 100 м. На какую скорость рассчитан вираж?
Задача 128. Средняя высота спутника над поверхностью Земли 1700 км. Определить его скорость и период вращения.
Задача 129. С увеличением высоты полета спутника его скорость уменьшилась с 7,79 до 7,36 км/с. Определить, на сколько изменились период вращения спутника и удаленность его от земной поверхности.
Задача 130. Определить период вращения искусственного спутника вблизи планеты, которую можно принять за однородный шар плотностью ρ.
Задача 131. Спутник вывели на круговую орбиту со скорость v над полюсом Земли. Найти расстояние от спутника до поверхности Земли.
Задача 132. Найти массу Земли, если спутник, движущийся в ее экваториальной плоскости с запада на восток по круговой орбите радиуса R=2∙104 км, появляется над некоторым пунктом на экваторе через каждые τ=11,6 ч.
Задача 133. Подводная лодка, не имевшая хода, получив небольшую плавучесть р = 0.01 mg, начинает подниматься с глубины H=100 м. При этом начавший работать двигатель обеспечивает постоянную горизонтальную силу тяги Т = 0.01 mg. Силу сопротивления принять пропорциональной первой степени скорости V и равной R = –0.1 mV. Определить траекторию лодки и расстояние, пройденное ею по горизонтали к моменту всплытия.
Задача 134. Определить закон движения x (t), y (t) тяжелой материальной точки M массы m = 5 кг, притягиваемой к неподвижному центру O силой, прямо пропорциональной расстоянию до него. Движение происходит в пустоте, сила притяжения F=-k2mOM, k = 20 с –1. Ускорение свободного падения g = 9.8 м/с 2. В начальный момент времени (t=0) 
, v x 0 = 200 м/с, 
. Ось Ox горизонтальна, а ось Oy направлена по вертикали вверх.
Задача 135. Подводная лодка, не имевшая хода, находилась в надводном положении на расстоянии H=100 м от дна. Получив отрицательную плавучесть р = 0.1 mg, она начинает уходить от преследования на очень тихом ходу, который обеспечивается малой постоянной горизонтальной силой тяги двигателя T = 0.001 mg. Горизонтальной компонентой силы сопротивления можно пренебречь, а ее вертикальную составляющую принять равной R = –0.05 mg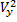 
, гдеVy – вертикальная скорость погружения лодки. Определить закон движения лодки и расстояние, пройденное ею по горизонтали к моменту, когда она ляжет на дно.
Задача 136. Точка M массы m = 5 кг движется под действием силы отталкивания от неподвижного центра O, изменяющейся по закону F=k2mr, где k = 20 c –1, r – радиус-вектор точки. В начальный момент точка M имела координаты M 0 (a,0), a = 24 м, и скорость v0 с проекциями v x 0 = 0, v y 0 = 4 м/с. Определить закон движения и траекторию точки M. Силой тяжести Земли пренебречь.
Задача 137. Подводная лодка, не имевшая хода, получив небольшую положительную плавучесть р = 0.001 mg, начинает подниматься с глубины H=150 м. При этом начавший работать двигатель обеспечивает постоянную горизонтальную силу тяги T=mg. Вертикальной компонентой силы сопротивления можно пренебречь, а ее горизонтальную составляющую принять равной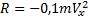 
, гдеVx – горизонтальная скорость лодки. Определить траекторию движения лодки и расстояние, пройденное ею по горизонтали к моменту всплытия.
Задача 138. Подводная лодка, двигавшаяся в надводном положении c малой скоростью U 0 = 0.5 м/с, получив отрицательную плавучесть р = 0.5 mg, начала срочное погружение с выключенными двигателями. Горизонтальной компонентой силы сопротивления можно пренебречь, а ее вертикальную составляющую принять равной R = –0.05 mg 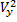, гдеVy – вертикальная скорость погружения лодки. Определить закон движения лодки и расстояние, пройденное ею по горизонтали к моменту, когда она погрузится на глубину H=150 м.
Задача 139. Телу M массы m = 8 кг, принимаемому за материальную точку и находящемуся на гладкой наклонной плоскости с углом наклона к горизонту 
= 30° (рис. 39), сообщена начальная скорость v0 = 18 м/с, направленная под углом 
= 45° к оси x и лежащая в плоскости ху. Ось y горизонтальна. Ускорение свободного падения g = 9.8 м/с 2. Определить закон движения тела по наклонной плоскости x (t), y (t).
Рис.39
Задача 140. Подводная лодка, двигавшаяся в надводном положении со скоростью U 0 = 0.5 м/с, получив отрицательную плавучесть р = 0.1 mg, начала погружение с выключенными двигателями. Силу сопротивления принять пропорциональной первой степени скорости V и равной R=-0,05mV.Определить траекторию движения лодки и расстояние, пройденное ею по горизонтали к моменту, когда она погрузится на глубину H=150 м.
Задача 141. Наибольшая горизонтальная дальность полета снаряда 
м достигается при угле бросания 
по отношению к горизонту. Определить, чему равны начальная скорость снаряда v0 и . Ускорение свободного падения g = 9.8 м/с 2. Сопротивлением воздуха пренебречь. Начальная скорость снаряда v0 при вылете из канала ствола орудия фиксирована.
Задача 142. Береговое орудие, расположенное на высоте H=150 м над уровнем моря, стреляет снарядами, имеющими при вылете из ствола скорость U 0 = 1500 м/с. Определить дальность поражения цели при горизонтальном выстреле и закон движения снаряда x (t), y (t), если вертикальной компонентой силы сопротивления можно пренебречь, а ее горизонтальную составляющую принять равной 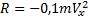, гдеVx – горизонтальная скорость снаряда.
Задача 143. Определить закон движения x (t), y (t) материальной точки M массы m = 8 кг, притягиваемой к неподвижному центру O силой, прямо пропорциональной расстоянию до него. Движение происходит в пустоте, сила притяжения равна F=-k2mOM, k = 12 c –1. В начальный момент времени (t=0) х 0 = 18 м, 
, v y 0 = 6 м/с. Силой тяжести Земли пренебречь.
Задача 144. Материальная точка массы m движется по гладкой горизонтальной плоскости Oxy под действием силы, направленной параллельно оси x. Модуль силы изменяется по закону F=3t2. Начальная скорость 
м/с направлена под углом 
к линии действия силы. Получить уравнение траектории точки y (x).
Задача 145. Точка M массы m = 8 кг движется под действием силы отталкивания от неподвижного центра O, изменяющейся по закону F=k2mr, где k = 12 c –1, r – радиус-вектор точки. Ускорение свободного падения g = 9.8 м/с 2. В начальный момент времени (t=0) х 0 = 20 м, , v y 0 = 50 м/с. Ось Ox горизонтальна, а ось Oy направлена по вертикали вверх. Определить закон движения x (t), y (t) и траекторию y (x) точки M.
Задача 146. Материальная точка массы m движется по гладкой горизонтальной плоскости Oxy под действием силы, направленной параллельно оси у (см. рис. 39). Модуль силы изменяется по закону F=4t3. Начальная скорость V0=5 м/с направлена перпендикулярно к линии действия силы. Найти закон движения x (t), y (t) и уравнение траектории точки y = y (x).
Задача 147. Телу M массы m = 20 кг, принимаемому за материальную точку и находящемуся на гладкой наклонной плоскости с углом наклона к горизонту = 60° (см. рис. 39), сообщена начальная скорость v0 = 2 м/с, направленная под углом = 30° к оси x и лежащая в плоскости ху. Ось y горизонтальна. Ускорение свободного падения g = 9.8 м/с 2. Определить закон движения тела по наклонной плоскости x (t), y (t).
Задача 148. При угле бросания = 60° по отношению к горизонту снаряд имеет горизонтальную дальность полета 
м. Определить, чему при этом равна начальная скорость снаряда v0. Найти также горизонтальную дальность и максимальную высоту траектории при угле бросания 30°. Ускорение свободного падения g = 9.8 м/с 2. Сопротивлением воздуха пренебречь. Начальная скорость снаряда v0 при вылете из канала ствола орудия фиксирована.
Задача 149. Определить закон движения x (t), y (t) тяжелой материальной точки M массы m = 6 кг, притягиваемой к неподвижному центру O силой, прямо пропорциональной расстоянию до него. Движение происходит в пустоте, сила притяжения равна F=-k2mOM, k = 8 c –1. Ускорение свободного падения g = 9.8 м/с 2. В начальный момент времени (t=0) х 0 = 24 м, Vx0=0, у 0 = 40 м, Vy0=0. Ось Ox горизонтальна, а ось Oy направлена по вертикали вверх.
Задача 150. Точка M массы m = 4 кг движется под действием силы отталкивания от неподвижного центра O, изменяющейся по закону F=k2mr, где k = 10 c –1, r – радиус-вектор точки. Ускорение свободного падения g = 9.8 м/с 2. В начальный момент времени (t=0) х 0 = 2 м, v х 0 = 4 м/с,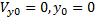 
. Ось Ox горизонтальна, а ось Oy направлена по вертикали вверх. Определить закон движения x (t), y (t) и траекторию y (x) точки M.
Задача 151. Парашютист массы mпадает с раскрытым парашютом на Землю в спокойном воздухе вертикально с установившейся постоянной скоростью V0=5 м/с. На высоте h=100 м над поверхностью Земли он, натянув стропы, приобретает горизонтальную скорость 
м/с. Определить величину горизонтального отклонения парашютиста от первоначального направления его движения в момент приземления и закон его движения, если при дальнейшем спуске он удерживает стропы в том же положении. Горизонтальная компонента силы сопротивления, действующая на парашютиста в воздушном потоке, Rx = –0.01 mVx, где Vx – горизонтальная скорость парашютиста. Изменением вертикальной компоненты силы сопротивления, вызванной наклоном купола парашюта, пренебречь.
Задача 152. Стартуя с поверхности Земли, реактивный снаряд массы M=100 кг движется в течение первых 10 с под действием силы тяги F=5000 H, направленной под углом 
к горизонту (
). Затем сила тяги отключается. Определить траекторию движения снаряда и его дальность полета. Силой сопротивления воздуха пренебречь.
Задача 153. Телу M массы m = 28 кг, принимаемому за материальную точку и находящемуся на гладкой наклонной плоскости с углом наклона к горизонту = 45° (см. рис. 39), сообщена начальная скорость v0 = 34 м/с, направленная под углом = 30° к оси x и лежащая в плоскости ху. Ось y горизонтальна. Ускорение свободного падения g = 9.8 м/с 2. Определить закон движения тела по наклонной плоскости x (t), y (t).
Задача 154. Подводная лодка, не имевшая хода, получив небольшую положительную плавучесть p = 0.01 mg, начинает подниматься с глубины H=100 м. При этом начавший работать двигатель обеспечивает постоянную горизонтальную силу тяги Т = 0.01 mg. Вертикальной компонентой силы сопротивления можно пренебречь, а ее горизонтальную составляющую принять равной R = –0.01 mVx, гдеVx – горизонтальная скорость лодки. Определить траекторию движения лодки y (x) и расстояние, пройденное ею по горизонтали к моменту всплытия.
Задача 155. При угле бросания 
= 42° по отношению к горизонту снаряд имеет горизонтальную дальность полета 
м. Определить, чему равна начальная скорость снаряда v0 при вылете из канала ствола орудия. Найти также горизонтальную дальность полета снаряда и время полета снаряда до цели при угле бросания = 35° и той же начальной скорости v0. Ускорение свободного падения g = 9.8 м/с 2. Сопротивлением воздуха пренебречь.
Задача 156. Определить угол наклона ствола орудия к горизонту, чтобы поразить цель, обнаруженную на той же горизонтальной плоскости, что и орудие, на расстоянии 
м. Дополнительно определить максимальную высоту траектории и время полета снаряда до цели. Начальная скорость снаряда v0 = 600 м/с. Ускорение свободного падения g = 9.8 м/с 2. Сопротивлением воздуха пренебречь.
Задача 157. Определить зависимость горизонтальной дальности полета снаряда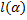 
, максимальной высоты его траектории 
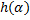и времени полета 
от угла наклона ствола орудия к горизонту. Найти также значения этих величин для = 38°. Начальная скорость снаряда v0 = 980 м/с. Ускорение свободного падения g = 9.8 м/с 2. Сопротивлением воздуха пренебречь.
Задача 158*. Считая Землю шарообразной, найти зависимость ускорения силы тяжести Земли от широты местности. Вычислить g на полюсе, экваторе и на широте Одессы
Задача 159*. Найти изменение ускорения силы тяжести тела на глубине h от поверхности Земли. На какой глубине ускорение силы тяжести составит 0,3 от ускорения силы тяжести на поверхности Земли? Плотность земли считать постоянной. Считать, что со стороны вышележащего слоя тело не испытывает никакого притяжения.
Задача 160*. Воздушный шар массы m под действием выталкивающей силы F = 1.1 mg начинает подъем. Горизонтальная компонента силы сопротивления воздуха пропорциональна квадрату горизонтальной компоненты скорости шара относительно воздуха: Rx = –0.1 m 
, где Vx – его горизонтальная относительная скорость. Вертикальной компонентой силы сопротивления воздуха пренебречь. Определить закон движения шара x (t), y (t), если дует горизонтальный ветер со скоростью 
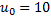м/с.
Задача 161*. Тело M массы m = 8 кг находится под действием двух сил притяжения F1=-k2mO1M, F2=-k2mO2M, k = 20 c –1, направленных к двум неподвижным центрам O 1 (– a,0) и O 2 (a,0), a = 24 м. Движение начинается в точке A 0 (–2 a,0) со скоростью Vx0=0, v у 0 = 18 м/с. Определить закон движения x (t), y (t) и траекторию y (x) точки M. Найти моменты времени, когда она пересекает ось Ox, и вычислить ее координаты в эти моменты времени. Силой тяжести пренебречь.
Задача 162*. Тело M массы m = 2 кг находится под действием двух сил притяжения F1=-k2mO1M, F2=-k2mO2M, k = 120 c –1, направленных к двум неподвижным центрам O 1 (– a,0) и O 2 (a,0), а = 12 м. Ускорение свободного падения g = 9.8 м/с 2. Движение начинается в точке A 0 (2 a,0) со скоростью Vx0=0, v у 0 = 12 м/с. Ось Ox горизонтальна, а ось Oy направлена по вертикали вверх. Определить закон движения x (t), y (t) и траекторию y (x) точки M. Найти моменты времени, когда она пересекает ось Ox, и вычислить ее координаты в эти моменты времени.
Задача 163*. Материальная точка M массы m движется в вертикальной плоскости под действием силы тяжести, постоянной горизонтальной силы тяги F = 0.1 mg, силы сопротивления R = –0.1 mV,где V – скорость точки, и вертикальной подъемной силы Q = 2 m v x, где Vx – горизонтальная скорость точки. Получить закон движения точки вдоль вертикальной оси y, если в начальный момент времени (t=0) ее положение совпадало с началом системы координат, а ее начальная скорость горизонтальна и равна V0=5 м/с.
Задача 164*. Тело массы m на высоте H=500 м над поверхностью Земли имело скорость V0=7 м/с, направленную вертикально вниз. Затем оно попадает в воздушный поток, который движется горизонтально с постоянной скоростью 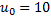м/с. В результате на него действует сила 
где V r – скорость тела относительно потока. Определить величину горизонтального отклонения тела от первоначального направления его движения в момент падения на Землю.
Задача 165*. Парашютист массы m, совершая затяжной прыжок, падает на Землю в спокойном воздухе вертикально с установившейся постоянной скоростью V0=40 м/с. На некоторой высоте от поверхности Земли он попадает в воздушный поток, который движется горизонтально с постоянной скоростью u 0 = 0.5 м/с,и в это же время открывает парашют. Горизонтальная компонента силы, действующая на парашютиста в воздушном потоке, Rx = –0.01 mVrx, где Vrx – горизонтальная скорость тела относительно потока воздуха. Вертикальная компонента силы сопротивления, действующая на парашютиста, Ry = –0.1 m 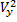, где Vy – его вертикальная скорость. Определить закон движения парашютиста x (t), y (t) после раскрытия парашюта.
Задача 166*. Материальная точка M массы m движется в вертикальной плоскости под действием силы тяжести, постоянной горизонтальной силы тяги F = 0.2 mg, силы сопротивления R = –0.1 mV, где V – скорость точки, и вертикальной подъемной силы Q=2mVx, где Vx – горизонтальная скорость точки. Получить закон движения точки в направлении горизонтальной оси x, если в начальный момент времени (t=0) ее положение совпадало с началом системы координат, а ее начальная скорость горизонтальна и равна V0=5 м/с.
Задача 167*. Парашютист массы m с раскрытым парашютом падает вертикально с установившейся постоянной скоростью V0=5 м/с. На высоте h=100 м над поверхностью Земли он попадает в воздушный поток, который движется горизонтально с постоянной скоростью 
м/с. Определить величину горизонтального отклонения парашютиста от первоначального направления его движения в момент приземления и закон его движения x (t), y (t). Горизонтальная компонента силы сопротивления, действующая на парашютиста в воздушном потоке, Rх = –0.01 mVx, где Vx – горизонтальная скорость парашютиста относительно потока воздуха.
