Координатным способом обычно определяют движение точки, не ограниченные какими-либо условиями, связями. Если на движение точки наложены ограничения, на скорость или координаты, то определить такое движение координатным способом совсем не просто. Удобнее использовать естественный способ задания движения.
Определим, например, движение точки по заданной неподвижной линии, по заданной траектории (рис. 23).
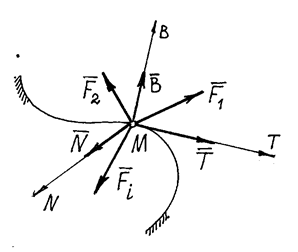
Рис.23
На точку М кроме заданных активных сил 
, действует реакция линии. Показываем составляющие реакции 
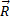по естественным осям 
.
Составим основное уравнение динамики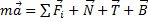 
и спроектируем его на естественные оси
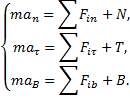
Так как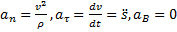 
, то получим дифференциальные уравнения движения, такие
Здесь сила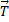 
- сила трения. Если линия, по которой движется точка, гладкая, то Т = 0 и тогда второе уравнение будет содержать только одну неизвестную – координату s:
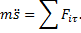
Решив это уравнение, получим закон движения точки s=s(t), а значит, при необходимости, и скорость и ускорение. Первое и третье уравнения (5) позволят найти реакции 
и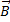 
.
|
Рис.24
Схема решения задачи та же, что и при координатном способе (пример 15). Отличие лишь в выборе осей. Здесь оси N и Т движутся вместе с лыжником. Так как траектория – плоская линия, то ось В, направленную по бинормали, показывать не нужно (проекции на ось В действующих на лыжника сил будут равны нулю).
Дифференциальные уравнения по (5) получим такие
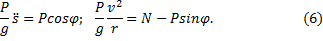
Первое уравнение получилось нелинейным: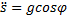 
. Так как 
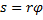, то его можно переписать так: 
. Такое уравнение можно один раз проинтегрировать. Запишем 
. Тогда в дифференциальном уравнении переменные разделятся: 
. Интегрирование дает решение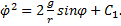 
Так как при t = 0: 
и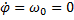 
, то С 1= 0 и 
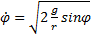, а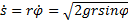 
.
К сожалению, в элементарных функциях второй интеграл найти невозможно. Но и полученное решение позволяет сделать некоторые выводы. Можно найти скорость лыжника в любом положении как функцию угла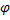 
. Так в нижнем положении, при 
. А из второго уравнения (6) при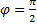 
можно определить давление: 
. То есть давление на лыжника в нижнем положении равно его трехкратному весу.
Пример 24. Научно-исследовательская подводная лодка шарообразной формы и массы m = 1.5∙105 кг начинает погружаться с выключенными двигателями, имея горизонтальную скорость v х 0 = 30 м/с и отрицательную плавучесть Р 1 = 0,01 mg, где P1=mg+Q – векторная сумма архимедовой выталкивающей силы Q и силы тяжести mg, действующих на лодку (рис. 24.1). Сила сопротивления воды R=-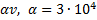 
кг/с. Определить уравнения движения лодки и ее траекторию.
Рис.24.1
Решение. Начало координат выберем в начальном положении лодки, ось Ox направим горизонтально, а ось Oy – вертикально вниз (см. рис. 24.1). На лодку действуют три силы: P=mg – вес лодки, Q – архимедова выталкивающая сила, причем mg>Q, и сила сопротивления R. Лодку примем за материальную точку M. Тогда второй закон Ньютона запишется так: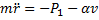 
. В проекциях на оси Ox и Oy он будет иметь вид: 
. Перепишем эти уравнения в форме системы уравнений первого порядка
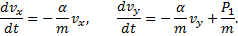
Интегрируя их методом разделения переменных, получаем
После интегрирования и подстановки численных значений параметров и начальных данных находим
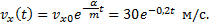
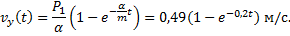
Закон движения находим из решения дифференциальных уравнений
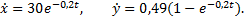
Он описывается соотношениями
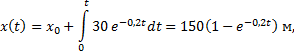
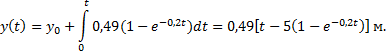
В заключение найдем траекторию y (x). Для этого из первого уравнения выразим время t через координату х
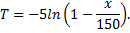
Подставляя это выражение во второе уравнение, находим
Пример 25. Точка, имеющая массу m, движется из состояния покоя по окружности радиуса R с постоянным касательным ускорением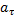 
(рис.25). Определить действующую на точку силу в момент, когда она пройдет по траектории расстояние 
.
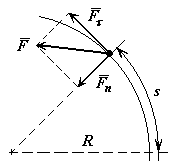
Рис.25
Применяя дифференциальные уравнения движения точки в проекциях на естественные оси, имеем:
;
Так как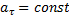 
, то 
;
,
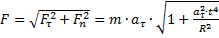; следовательно 
;
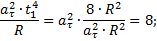
следовательно
.
.
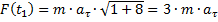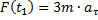