Известны две основные схемы дискретного начисления процентов за фиксированные в договоре интервалы времени: схема простых процентов (simple interest) и схема сложных процентов (compound interest).
Простые проценты представляют собой величину прирастания определенной суммы Р, увеличивающейся за определенный срок (единичный промежуток начисления Т=1) на некоторый процент (по ставке r, представленной в виде дроби) от начальной суммы P, т.е. на rP. Последовательность наращенных сумм P, F1, F2, …, Fn за n промежутков начисления представляет собой арифметическую прогрессию с начальным членом P и разностью rP. Таким образом, к концу n-го промежутка начисления наращенная сумма рассчитывается по формуле: F=P +Pr +Pr+…+Pr=P +Prn, и следовательно,
Fn= P(1+nr) (1).
(1+nr) – называют множителем наращения. Если ставка r измеряется в процентах, то для ее представления в виде дроби следует r поделить на 100.
Наращение по простым процентам применяется при обслуживании сберегательных вкладов с ежемесячной выплатой процентов и вообще в тех случаях, когда проценты не присоединяются к сумме долга, а периодически выплачиваются кредитору. Простые проценты применяют при выдаче краткосрочных ссуд (срок до одного года с однократным начислением процентов).
Сложные проценты представляют собой величину прирастания определенной суммы, увеличивающейся за определенный срок (единичный промежуток начисления) на некоторый процент с учетом получения процентов на проценты. Таким образом, каждая следующая сумма при наращении сложных процентов по ставке r возрастает на долю r от предыдущей и рассчитывается по формуле:
Fn=P(1+ r)n. (2)
Последовательность наращенных сумм P, F1, F2, …, Fn за n промежутков начисления представляет собой геометрическую прогрессию с начальным членом P и знаменателем прогрессии (1+r).
Процентные деньги (проценты) – это величина дохода,
равная Дn=Fn-P (3), т.е. разности между наращенной суммой и начальной.
Норма процента рассчитывается по формуле (4):
 |
Правило 72. Если процентная ставка есть a, то удвоение капитала по такой ставке происходит примерно за 72/a лет. Это правило применяется для небольших ставок, вычисляемых по сложным процентам.
При выводе формул 1, 2 предполагалось, что n измеряется в годах, а r является годовой процентной ставкой. Эту формулы можно применить и при других периодах начисления. Необходимо только следить за соответствием длины периода и процентной ставки (размерность каждого периода nk должна быть согласована с размерностью процентной ставки rk.
В том случае, когда сложные проценты начисляются m-раз в году, а наращение капитала происходит за n лет, где n – целое число, формула нахождения наращенной суммы примет следующий вид:
 (5).
(5).
Можно сделать некоторые выводы для сложных процентов:
Ø Проценты, полученные за год по ставке r не эквивалентны процентам, полученным за год по ставке r/12 в месяц;
Ø чем чаще идет начисление по схеме сложных процентов, тем больше итоговая накопленная сумма.
Для облегчения расчетов составлены таблицы мультиплицирующих множителей, которые показывают, во сколько раз возрастет за n лет сумма, положенная в банк под r процентов годовых: FM(n,r)=(1+r)n. Величина FM(n,r) есть будущая стоимость одной денежной единицы (один рубль, один доллар, одна иена и т.п.)– через n лет при ставке процента r.
Достаточно обыденными являются финансовые контракты, заключаемые на период, отличающийся от целого числа лет. В этом случае проценты могут начисляться с помощью следующих методов:
Ø По схеме сложных процентов 
Ø По смешанной схеме (используется схема сложных процентов для целого числа лет и схема простых процентов для дробной части года): 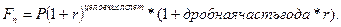
В том случае, когда продолжительность финансовой операции рассчитывается в днях, однозначного определения процента и других параметров финансовой операции нет. Решение будет зависеть от того, как рассчитывается продолжительность года и продолжительность периода финансовой операции.
Таким образом, существует два варианта процентов: точный процент и обыкновенный процент.
При расчете точного процента (exact interest) берется точное число дней в году (365, 366), в квартале (89 – 92), в месяце (28 – 31).
При расчете обыкновенного процента (ordinary) берется приближенное число дней в году (360), в квартале (90), в месяце (30).
Продолжительность периода финансовой операции (например, ссуды) исчисляется также двумя способами: расчет по дням (берется точное число дней) и расчет с приближенным числом дней в месяце (30).
Следовательно, можно выделить три способа расчета процентов:
I. Обыкновенный процент с приближенным числом дней (360/360). Такой способ расчета практикуется в Германии, Дании, Швеции.
II. Обыкновенный процент с точным числом дней (365/360 или АСТ/360). Такой способ расчета практикуется в Бельгии и Франции.
III. Точный процент с точным числом дней (365/365 или АСТ/АСТ). Такой способ расчета практикуется в Великобритании и США.
В российской практике можно встретиться с различными схемами начисления процентов. Эффект от выбора зависит от суммы финансовой операции. Понятно, что использование обыкновенных процентов с точным числом дней ссуды, как правило, дает больший результат, чем применение обыкновенных процентов с приближенным числом дней ссуды.
Пример 1.1. Депозит в 200 тыс. руб. положен в банк на 4 года под 15% годовых. Найти наращенную сумму, если ежегодно начисляются сложные проценты.
Решение. Применим формулу (2) и получим F4=200000 (1+0,15)4.
Пример 1.2. Годовая ставка простых процентов равна 8,3%. Через сколько лет начальная сумма удвоится?
Решение. Обозначим начальную сумму через Р. Тогда Р*(1+n*0,083)³ 2Р, т.е. 1+n*0,083)³ 2, n³ 1/0,083. С точностью до целых – через тринадцать лет.
Пример 1.3. Пусть P=1000, r = 10%- сложные проценты. Найти наращенную сумму за за n=3 промежутка начисления.
Решение. Р=1000; F1=1000 (1+0,1)1=1100; F2,=1100*1,1=1210; F3=1210*1,1=1331,1.
Пример 1.4. Годовая ставка сложных процентов равна r =8%. Через сколько лет начальная сумма удвоится?
Решение. Р(1+0,08)n³2Р; (1+0,08)n ³ 2; n* ln(1,08)³ ln2;
n³ (ln(2)/ln(1,08))=9.
Пример 1.5. М.Е. Салтыков-Щедрин описывает в «Господах Головлевых» такую сцену: «Порфирий Владимирович сидит у себя в кабинете, исписывая цифирными выкладками листы бумаги. На этот раз его занимает вопрос: сколько было бы у него теперь денег, если бы маменька подаренные ему при рождении дедушкой «на зубок» сто рублей не присвоила себе, а положила в ломбард на имя малолетнего Порфирия? Выходит, однако, немного: всего восемьсот рублей».
Требуется рассчитать по приведенным цифрам, какой процент платил в то время ломбард по вкладам. Возраст Порфирия в момент его расчетов примем равным пятидесяти годам.
Решение. В нашем примере нужно воспользоваться формулой сложных процентов, обозначив через х – искомый процент по вкладам (годовую ставку сложных процентов), и взяв n=50.
Получим: 800=100(1+х)50.
Логарифмируя с помощью таблицы логарифмов, получим решение следующим образом: lg800=lg100+50lg(1+x).

Антилогарифм 1+х=1,039. Тогда х=3,9%.
Пример 1.6. Чему равна будущая стоимость одной денежной единицы через 9 лет при ставке процента 10%.
Решение. Так как n=9, r=10%, то согласно таблице мультиплицирующих множителей М(9,10)=2,358.
Пример 1.7. Предоставлена ссуда в размере 7 тыс. руб. 10 февраля с погашением 10 июня под 20% годовых (простая ставка, год не високосный). Рассчитать различными способами сумму к погашению F.
Решение.
1. Подсчитаем точное число дней, которые берется в расчет при выплате процентов. По табл. 161-41=120 (дней)
2. Подсчитаем приближенное число дней ссуды: t= 18 дней февраля (59-41) + 90 дней (март-июнь) + 10 дней июня=118 дней.
3. АСТ/АСТ F=7 (1+120/365*0,2)=7460руб.
4. 360/360 F=7 (1+118/360*0,2)=7459руб.
5. 365/360 F=7 (1+120/360*0,2)=7467руб.
Пример 1.8. 14 марта в банк положили сумму 1000 у.е. до востребования под ставку 12% годовых сложных процентов. Какую сумму снимет вкладчик 1 сентября?
Решение. Однозначного решения нет. Выберем способ расчета 360/360, т.е. в году 360 дней, в месяце 30 дней.
1) Найдем, какую долю от года составляет промежуток времени, в течение которого вклад хранился в банке: t=(30 дней * 5 месяцев +17 дней) / 360. Дни считаем так: из порядкового номера последнего дня вычитается порядковый номер первого дня.
2) Найдем, какую сумму снимет вкладчик 1 сентября: Fn= 1000 *(1+0,12)227/360.
Пример 1.9. Пусть сумма начального вклада Р=750 у.е. наращивается по годовой ставке r=20%. Принятая схема начисления: по простым процентам. Подсчитать проценты за n=4 промежутков начисления (лет). Представить последовательность наращенных сумм за 4 года.
Решение. Так как под процентами (процентными деньгами) понимают величину дохода (приращение денег) In= Fn -P, то сначала найдем Fn
Fn – это наращенная за n лет сумма, которая находится по формуле Fn =P + n´r´P=Р(1+nr), где r – дробное измерение ставки. Таким образом, F4=750(1+4´0,2)=750 1,8=1350.
Следовательно, I4= F4-P=1350-750=600 (у.е.) – процентные деньги за 4 года.
Последовательность наращенных сумм в случае простых процентов представляет арифметическую прогрессию: F1= Р(1+1´r)= 750(1+0,2)= 900; F2= Р(1+2´r)= 750(1+0,4)= 1050; F3= Р(1+3´r)= 750(1+0,6)= 1200; F4 = Р(1+4´r)=750(1+0,8)=1350, каждый следующий элемент последовательности отличается от предыдущего на 150 у.е., т.е. приросты денежных сумм для любого периода составляют 150 у.е. –постоянную долю от первоначальной суммы Р=750 у.е.
Пример 1.10. Предприниматель получил в банке ссуду в размере 25 тыс. руб. сроком на 6 лет на следующих условиях: для первого года процентная ставка равна 10% годовых, на следующие 2 года устанавливается маржа в размере 0,4% и на последующие годы маржа равна 0,7%. Найти сумму, которую предприниматель должен вернуть в банк по окончании срока ссуды.
Решение. Р=25, n1=1, n2=2, n3=3; i1=0,1; i2=0,104; i3=0,107. Тогда F6=25(1+0,1)(1+0,104)2(1+0,107)3=45,469 тыс.руб.
Пример 1.10. Семья положила Р=12 000 руб. на срочный вклад при срочной процентной ставке r=11% годовых (с учетом выплаты процентов на проценты). Сколько денег семья получит через два года, при условии, что в течение двух лет деньги сниматься со сберкнижки не будут?
Решение. Выплата процентов на проценты означает, что одна и та же ставка r начисляется для каждого следующего промежутка начисления на результат предыдущего начисления (наращенную сумму за предыдущий период начисления или, что т о же самое, на сумму, наращенную на начало данного периода начисления). По формуле сложных процентов наращенная сумма за n лет составит величину Fn= Р(1+r)n. Следовательно, в нашем случае при n=2 F2=Р(1+r)2=12000 (1+0,11)2=12000´1,112=1,2321´12000=14785,2
Пример 1.11. В банк вложены деньги в сумме 5 тыс. руб. на 2 года с полугодовым начислением процентов под 20% годовых. Найти величину капитала через 2 года. Проанализировать, изменится ли величина капитала к концу двухлетнего периода, если проценты будут начисляться ежеквартально?
Решение. В этом случае начисление процентов производится 4 раза по ставке 10%, тогда Р=5, n=2, m=2, r(m) = r(2) = 0,2 и
1) 
3) В этом случае начисление происходит 8 раз, m=4, n=2 по ставке 5% (20%/4) и 
Пример 1.12. Банк предоставил ссуду в размере 10 тыс. руб. на 30 мес. под 30% годовых на условиях ежегодного начисления процентов. Какую сумму предстоит вернуть банку по истечении срока?
Решение. n=2,5; целое число лет=2; дробная часть года=0,5.
По схеме сложных процентов F2,5=10(1+0,3)2+0,5=19,269 тыс.руб.
По смешанной схеме F2,5=10(1+0,3)2 (1+0,5*0,3)=19,435 тыс. руб.
Т.о. для банка смешанная схема начисления более выгодная.






