Поскольку число одной из групп в наблюдениях количества переработанной руды и содержания металла в руде равно нулю, то необходимо провести вторичную группировку, уменьшая количество интервалов до 4-х (табл. 3.3, 3.4; рис. 3.2).
Таблица 3.1
| Параметры | Количество переработанной руды | Содержание Ме в руде | Выход конц. | Содержание Ме в конц. | Содержание S в конц. | Извлечение | Потери | |
| Содержание Ме в хвост. | Содержание Ме в сульф. | |||||||
| Max | 314,67 | 0,96 | 1,15 | 68,15 | 0,54 | 80,60 | 0,22 | 1,02 |
| Min | 139,00 | 0,45 | 0,40 | 63,81 | 0,27 | 66,63 | 0,11 | 0,28 |
| Max–Min | 175,67 | 0,51 | 0,75 | 4,35 | 0,27 | 13,97 | 0,11 | 0,78 |
| k | ||||||||
| D | 35,13 | 0,10 | 0,15 | 0,87 | 0,05 | 2,79 | 0,02 | 0,10 |
| Ср.значение | 253,68 | 0,58 | 0,65 | 66,50 | 0,43 | 73,56 | 0,14 | 0,60 |
| Mo | 234,67 | 0,52 | #Н/Д | #Н/Д | 0,54 | 72,57 | 0,14 | 0,65 |
| Me | 264,33 | 0,57 | 0,62 | 66,89 | 0,44 | 73,87 | 0,14 | 0,59 |
| Дисперсия | 1735,79 | 0,01 | 0,02 | 1,45 | 0,01 | 9,70 | 0,00 | 0,04 |
| Стандартное отклонение | 41,66 | 0,10 | 0,14 | 1,20 | 0,08 | 3,11 | 0,02 | 0,20 |
| Средн.абсол. отклонен. от Me | 32,23 | 0,07 | 0,10 | 0,98 | 0,07 | 2,45 | 0,02 | 0,12 |
| Коэф-т вариации | 16,42% | 16,93% | 21,86% | 1,81% | 18,78% | 4,23% | 15,90% | 33,85% |
Таблица 3.2
| Количество переработанной руды | Содержание Ме в руде | Выход конц. | Содержание Ме в конц. | Содержание S в конц. | Извлечение | Потери | |||||||||
| Содержание Ме в хвост. | Содержание Ме в сульф. | ||||||||||||||
| Концы интервалов | Численность групп | Концы интервалов | Численность групп | Концы интервалов | Численность групп | Концы интервалов | Численность групп | Концы интервалов | Численность групп | Концы интервалов | Численность групп | Концы интервалов | Численность групп | Концы интервалов | Численность групп |
| 139,00 | 0,45 | 0,40 | 63,81 | 0,27 | 66,63 | 0,11 | 0,28 | ||||||||
| 174,13 | 0,55 | 0,55 | 0,32 | 69,43 | 0,13 | 0,44 | |||||||||
| 209,27 | 0,66 | 0,70 | 65,55 | 0,38 | 72,22 | 0,15 | 0,60 | ||||||||
| 244,40 | 0,76 | 0,85 | 66,41 | 0,43 | 75,01 | 0,17 | 0,75 | ||||||||
| 279,53 | 0,86 | 1,00 | 64,28 | 0,49 | 77,81 | 0,19 | 0,91 | ||||||||
| 314,67 | 0,96 | 1,15 | 68,15 | 0,54 | 80,60 | 0,22 | 1,07 |
 |








Рис. 3.1. Кривые распределения
Таблица 3.3
| Параметры | Количество переработанной руды | Содержание Ме в руде | |
| Max | 314,67 | 0,96 | |
| Min | 139,00 | 0,45 | |
| Max-Min | 175,67 | 0,51 | |
| k | |||
| D | 43,92 | ||
| Среднее значение | 253,68 | 0,58 | |
| Mo | 234,67 | 0,52 | |
| Me | 259,33 | 0,57 | |
| Дисперсия | 1795,65 | 0,01 | |
| Стандартное отклонение | 42,38 | 0,10 | |
| Среднее абсолютное отклонение от Me | 259,33 | 0,57 | |
| Коэффициент вариации | 16,70% | 17,22% |
Таблица 3.4
| Количество переработанной руды | Содержание Ме в руде | |||
| Концы интервалов | Численность групп | Концы интервалов | Численность групп | |
| 139,00 | 0,45 | |||
| 182,92 | 0,58 | |||
| 226,83 | 0,71 | |||
| 270,75 | 0,84 | |||
| 314,67 | 0,96 |

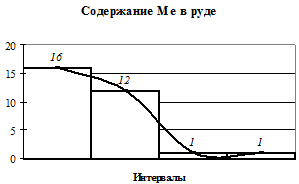
Рис. 3.2. Кривые распределения
Оценка параметров
При проведении практических исследований работу проводят по выборочным данным. Выборка, какой бы большой она не была, не может отождествляться с генеральной совокупностью. Кроме того, для выборочных значений не рассчитывается математическое ожидание. В выборочных исследованиях математическое ожидание совпадает со среднеарифметическим значением, однако среднеарифметическое и другие характеристики зависят от самой выборки.
Если взять другую характеристику – стандартное отклонение – то она тоже связанна с самой выборкой.
Существовали попытки оценить стандартное отклонение с помощью погрешности σ / √ n. Чем больше количество наблюдений n, тем меньше погрешность, поэтому предполагалось увеличивать выборку до бесконечности. Однако точность не увеличилась, так как стали появляться погрешности усреднения внутри самих задач и возникала проблема оценивания самих параметров.
Оценивание параметров ведется по двум направлениям:
1) нахождение точечных оценок параметров распределения;
2) нахождение интервалов оценивания параметров распределения.
Точечные оценки находятся следующим образом:
– точечная оценка среднеарифметического Z есть среднеарифметическое Ż.
– точечная оценка для дисперсии или несмещенная оценка дисперсии:
σ2 = ∑ (Ż – zi)2 / (N – 1),
где N – число наблюдений;
– оценка стандартного отклонения: σ = √ σ2
В интервальных оценках определяется:
– интервальная оценка для среднеарифметического: Ż ± t α σ / √ N, где t α – критерий Стьюдента (t α = 1,7 при уровне значимости α = 0,05 и числе степеней свободы n = N – 1 = 30 – 1 = 29);
– интервальная оценка для дисперсии
σ2(N – 1) / χ2 N – 1; α/ 2 ≤ σ2 ≤ χ2 N – 1; 1 – α/ 2,
где χ – критерий Пирсона.
Для данного случая
χ2 N – 1; α/ 2 = χ229; 0,25 = 45,7; χ2 N – 1; 1 – α/ 2 = χ229; 0,75 = 15,575.
Точечные и интервальные оценки рассмотренного случая приведены в табл. 3.5.
Расчеты позволяют сделать вывод о том, что несмещенная оценка дисперсии и оценка стандартного отклонения отличаются от полученных ранее дисперсий и стандартных отклонений.
Таблица 3.5
| Показатели | Точечные оценки | Интервальные оценки | ||
| для дисперсии | для стандартного отклонения | для среднеарифметического | для дисперсии | |
| Количество перерабатываемой руды | 1795,65 | 42,38 | 253,683 ± 13,152 | [1139,470; 3343,422] |
| Содержание Ме в руде | 0,01 | 0,10 | 0,58 ± 0,03 | [0,006; 0,019] |
| Выход конц. | 0,02 | 0,14 | 0,648 ± 0,45 | [0,013; 0,039] |
| Содержание Ме в конц. | 1,50 | 1,22 | 66,499 ± 0,380 | [0,951; 2,791] |
| Содержание S в конц. | 0,01 | 0,08 | 0,425 ± 0,025 | [0,004; 0,012] |
| Извлечение | 10,03 | 3,17 | 73,564 ± 0,983 | [6,365; 18,677] |
| Содержание Ме в хвост. | 0,001 | 0,02 | 0,143 ± 0,007 | [0,0003; 0,001] |
| Содержание Ме в сульф. | 0,04 | 0,21 | 0,600 ± 0,064 | [0,027; 0,079] |
Порядок выполнения работы
1. Изучить процедуру структурной группировки по данным табл. 1 приложения и предложенного метода.
2. Провести первичную структурную группировку для своего варианта, определенного в 1-й лабораторной работе.
3. Провести вторичную структурную группировку для своего варианта, определенного в 1-й лабораторной работе.
4. Провести оценку параметров кривых распределения на основе критериев Стьюдента и Пирсона и проанализировать полученные результаты в произвольной форме.
Контрольные вопросы
1. Как вычисляется критерий Стьюдента?
2. Что такое критерий Пирсона?
3. Что такое первичная структурная группировка?
4. Чем вторичная структурная группировка отличается от первичной?
5. Как строится интервальный ряд?
Лабораторная работа 4
Объемные группировки
Цель работы: познакомиться с построением таблиц совместимости группировок.




