Назначение корреляционного анализа

Задача корреляционного анализа состоит в количественном определении тесноты связи между двумя признаками и статистической оценке надежности установленной связи.

Условия применения анализа.

1. Корреляционный анализ можно применять только в том случае, когда данные наблюдения или эксперимента можно считать случайными и выбранными из нормальной совокупности.

2. Выборки из изучаемых генеральных совокупностей должны быть достаточно большого объема, так как для статистической методологии важное значение имеет закон больших чисел. Его содержание сводится к следующему: в массе индивидуальных явлений общая закономерность проявляется тем полнее и точнее, чем больше их охвачено наблюдением, только в этом случае происходит взаимопогашение индивидуальных значений признака от средней величины.

3. Отдельные наблюдения должны быть независимыми, то есть результаты, полученные в отдельном наблюдении, не должны содержать информацию о последующих наблюдениях и не должны быть связаны с будущими.

Алгоритм применения корреляционного анализа.

Основной оценкой для тесноты связи между переменными и 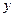служит выборочный коэффициент корреляции r, который определяется по формуле

Свойства выборочного коэффициента корреляции:

 

1. Коэффициент корреляции принимает значения на отрезке [-1; 1], то есть .

В зависимости от того насколько 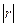приближается к 1, различают слабую, умеренную и сильную связь, то есть чем ближе 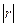к 1, тем теснее связь.

2. Если , то корреляционная связь между и 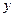представляет собой линейную зависимость.

Запишем более подробно формулу для вычисления коэффициента корреляции: .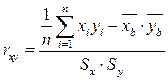

Замечание. Приведена формула для не сгруппированных данных.

Так как r вычисляется по данным выборки, то в отличие от генерального коэффициента корреляции, является величиной случайной. Если , то возникает вопрос, объясняется ли это действительно существующей линейной связью между и 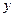или вызвано случайными факторами. Для выяснения этого вопроса проведем проверку статистической гипотезы.

: корреляционная связь отсутствует между переменными и 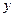, то есть .

Вычислим эмпирическое значение критерия . находим в таблице распределения Стьюдента критическое значение , определенное на уровне значимости и числом степеней свободы . Если , то гипотеза отвергается.

Пример. Фирма провела рекламную компанию. Через 10 недель фирма решила проанализировать эффективность этого вида рекламы, сопоставляя недельные объемы продаж с расходами на рекламу .

 

x
y

 

Для данных, приведенных в таблице найти выборочный коэффициент корреляции, проверить его значимость на уровне значимости .

 

Простейший способ задания статистических данных – набор пар чисел , где – выборка значений переменной , – выборка значений переменной .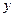

Однако очень часто экспериментальные данные задаются в виде корреляционной таблицы.

 

Yi Xi	12,5	147,5	22,5	27,5	nj
20-21 20,5		-	-	-
21-22 21,5	-		-	-
22-23 22,5	-			-
23-24 23,5	-	-
24-25 24,5	-	-	-
ni					n=20

В первой строке – значения , в первом столбце интервалы изменения 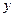, во втором – середина интервала. Центральная часть таблицы – частоты , соответствующие x_i и y_j. В последней строке 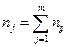, где в последнем столбце -, где – число значений , – число значений . Число всех значений .

Формула вычисления коэффициента корреляции для данных, заданных корреляционной таблицей

Пример. Для данных таблицы найти выборочный коэффициент корреляции, проверить его значимость на уровне α = 0,05.

Решение. Находим суммы:

 

 

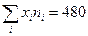
Вычислим:

Подставляя полученные суммы в (), найдем выборочный коэффициент корреляции

Проверим значимость r на уровне α = 0,05.

Для этого вычислим

 

по таблице распределения Стьюдента при k = n-2 = 18, находим 2,1. Так как > , то считаем значение r статистически значимым.

 

Регрессионный анализ.

 

Корреляционно-регрессионный анализ находит широкое применение в социологических исследованиях для прогнозирования уровня результативного признака путём подстановки в уравнение регрессии ожидаемых или планируемых значений факторного признака.

Как было отмечено в 7.1. при корреляционной зависимости между случайными корреляционными X и Y условное математическое одной из них зависит от значений другой.

Корреляционная зависимость может быть представлена в виде

Y₁(x) = M_x(Y); Y₂(y) = M_y(x).

Эти уравнения называются уравнениями регрессии, а их графики линиями регрессии.

При изучении статистической зависимости в социологии одним из главных моментов является установление формы зависимости, вида функции регрессии и её параметров, что является задачами регрессионного анализа.

Рассмотрим простейший случай линейной регрессии, когда функция Y линейна по X, то есть Y_x = a+bx.

Проведем случайную выборку. При значениях х₁, х₂, - x_n, мы наблюдаем значения y₁, y₂, - y_n. Отметим на плоскости O_xy точки с координатами (x₁, y₁), (x₂, y₂) – (x_n, y_n). Если связь между X и Y линейна, то точки группируются вокруг некоторой прямой линии y=a+bx. Точки не находятся прямо на линии, что неудивительно. Ведь помимо x на поведение y оказывают влияние и другие факторы.

Если в уравнение y= ax+b подставить значения x₁, x₂, x_n случайной выборки, то будут получены значения , которые будут отличаться от y₁, y₂, y_n.

Разница называется ошибкой. Значения коэффициентов a и b в уравнении y=a+bx необходимо подобрать так, чтобы минимизировать сумму . Для этого используется метод наименьших квадратов (МНК).

Согласно МНК неизвестные параметры a и b выбираются так, чтобы сумма квадратов отклонений выборочных значений y_i от их значений, вычисленных по формуле, была минимальной, то есть

 

На основании необходимого условия экстремума функции S(a,b) приравниваем к нулю её частные производные.

Получим систему:

После преобразований получим:

Это система двух уравнений с двумя неизвестными a и b. Решая её, находим:

 

 

 

Учитывая, что , , , , получим:

,

Коэффициент в уравнении регрессии Y по X называется коэффициентом регрессии и обозначается b_xy. Из определения выборочного коэффициента корреляции r следует, что .

Из полученных выражений для a и b можно получить формулы: , , поэтому линейное уравнение регрессии можно записать в обычной форме, принятой в математической статистике:

, или

.

Аналогичным образом, уравнение регрессии X на Y имеет вид:

.

Пример. Для зависимости Y от X, заданной в примере 8.1, записать уравнение линейной регрессии y_x=a+bx.

Решение:

1.Воспользуемся данными из предыдущего примера (см. 8.1)

 

 

 

,

Примеры для самостоятельного решения.

По результатам наблюдений найти оценки коэффициентов линейной регрессии.

 

											0,95
											0,99
											0,95
											0,99
											0,95

 

Ранговая корреляция.

 

Изложенный выше метод линейной корреляции является параметрическим, а значит, требует нормального закона распределения для X и Y, а также больших объемов выборок, что предполагает компьютерную обработку данных.

Альтернативой этому методу может служить метод ранговой корреляции Спирмена. Основанием для выбора метода ранговой корреляции служит его универсальность и простота. Метод применим к любым количественно измеренным или ранжированным данным, и позволяет подсчитывать корреляцию «вручную».

Назначение метода ранговой корреляции Спирмена.

Метод ранговой корреляции Спирмена позволяет определить тесноту (силу) и направление корреляционной связи между двумя признаками.

Ограничения.

1. По каждой переменной должно быть представлено не менее 5 наблюдений.

2. При большом количестве одинаковых рангов по одной или обеим переменным метод дает огрубленные результаты.

 

Гипотезы.

Н_о: Корреляция между двумя переменными X и Y не отличается от нуля.

Н₁: Корреляция между переменными X и Y статистически достоверно отличается от нуля.

Описание метода.

Для подсчета ранговой корреляции необходимо располагать двумя рядами значений, которые могут быть проранжированы. Для подсчета ранговой корреляции Спирмена необходимо вычислить квадрат разности рангов

d²= (ранг А- ранг B)².

Коэффициент ранговой корреляции Спирмена подсчитывается по формуле

N ― количество ранжируемых значений.

При заданном уровне значимости α и объеме выборок N в таблице 15 находим r_крит. ― критическое значение критерия Спирмена.

Если r_эмп.< r_крит., Н_о принимается.

Пример. Связаны ли между собой корреляционной зависимостью X и Y, выборочные значения которых представлены в таблице в 1 и 3 столбцах соответственно. Принять α =0,05.

X	RX	Y	RY	d= (Rx-Ry)	d2
			5,5	4,5	20,25
				-1
				-4
				-4
				-2
			5,5	-4,5	20,25

Решение.

, r_эмп < r _крит

Ответ: Н_о принимается.

Примеры для самостоятельного решения:

Выяснить, существует ли корреляционная зависимость между выборками.

											0,99
											0,95
											0,99
											0,95
											0,99

 

 

ЗАКЛЮЧЕНИЕ