ѕример 1. ¬ фирме провод€т проверку финансовой отчетности за 8 мес€цев, фиксируетс€ чиста€ (юридическа€) прибыль и прибыль с дополнительными издержками (экономическа€). ћожно ли считать статистически значимой равенство юридической и экономической прибыли? ”ровень значимости α = 0,01. 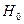 : юридическа€ прибыль не меньше экономической прибыли.
: юридическа€ прибыль не меньше экономической прибыли.
| мес€цы | экономическа€ прибыль | юридическа€ прибыль |
ќтвет: 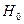 принимаетс€.
принимаетс€. 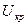 = 8,
= 8, 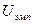 = 26.
= 26.
ѕример 2. ѕриводитс€ статистика рождаемости за один мес€ц по 9 городам ярославской области и 7 городам »вановской области. —редний уровень жизни в ярославской области выше. ћожно ли утверждать, что рождаемость зависит от уровн€ жизни. ѕроверить гипотезу 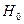 : уровень рождаемости в ярославской области не превышает уровень рождаемости в »вановской области. ѕрин€ть уровень значимости α = 0,05.
: уровень рождаемости в ярославской области не превышает уровень рождаемости в »вановской области. ѕрин€ть уровень значимости α = 0,05.
| город | ярославска€ обл. | »вановска€ обл. |
| - | ||
| - |
ќтвет: 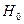 принимаетс€.
принимаетс€. 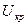 = 15,
= 15, 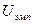 = 34.
= 34.
ѕример 3. ѕо рейтингу успеваемости (максимальное количество баллов) сравнивались студенты - контрактники и студенты - бюджетники в одной и той же учебной группе. ¬ 1 выборке Ц 15 студентов - бюджетников, во 2 выборке Ц 11 студентов-контрактников. ѕроверить гипотезу 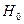 : рейтинг успеваемости студентов - бюджетников не выше, чем у контрактников. ѕрин€ть α = 0,05.
: рейтинг успеваемости студентов - бюджетников не выше, чем у контрактников. ѕрин€ть α = 0,05.
“аблица рейтинга успеваемости
| кол-во студентов | бюджет | контракт |
| - | ||
| - | ||
| - | ||
| - |
ќтвет: 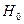 принимаетс€.
принимаетс€. 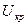 = 50,
= 50, 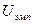 = 66,5.
= 66,5.
ѕример 4. ¬ рамках программы по профилактике безбилетного проезда в электропоездах была собрана статистика числа безбилетных пассажиров по направлению ћосква - ‘р€зино. —равнивались 2 группы Ц безбилетные пассажиры в утренние часы и пассажиры без билетов в вечерние часы. ƒанные собирались в течение 8 дней в утренние часы и 7 дней в вечерние. „исло безбилетных пассажиров утром: 58, 53, 46, 42, 40, 40, 37, 36; число безбилетных пассажиров вечером: 53, 42, 41, 40, 39, 35, 34. ѕроверить гипотезу 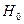 : утром число пассажиров, не оплативших свой проезд не больше, чем вечером. ѕрин€ть α = 0,05.
: утром число пассажиров, не оплативших свой проезд не больше, чем вечером. ѕрин€ть α = 0,05.
ќтвет: 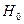 принимаетс€.
принимаетс€. 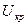 = 13,
= 13, 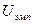 = 20.
= 20.
ѕример 5. ќценить различи€ между двум€ выборками ј и ¬ по уровню количественно измеренного признака с использованием U Ц критери€:
|
|
|
1). ѕрин€ть α = 0,05. ¬ыборка ј: 55, 54, 55, 52, 49, 47, 47, 36, 35. ¬ыборка ¬: 53, 53, 52, 50, 50, 49, 48, 45, 49.
ќтвет: √ипотеза 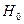 об отсутствии различий между выборками принимаетс€.
об отсутствии различий между выборками принимаетс€.
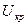 = 17,
= 17, 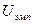 = 38,5.
= 38,5.
2). ѕрин€ть α = 0,01. ¬ыборка ј: 153, 147, 150, 145, 145, 146, 148, 147, 144, 138. ¬ыборка ¬: 146, 151, 149, 147, 145, 144, 137, 142, 138, 137.
ќтвет: √ипотеза 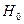 об отсутствии различий между выборками принимаетс€.
об отсутствии различий между выборками принимаетс€.
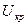 = 19,
= 19, 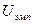 = 33,5.
= 33,5.
3). ѕрин€ть α = 0,05. ¬ыборка ј:75, 80, 82, 79, 90, 87, 76, 73, 89, 91, 81, 74. ¬ыборка ¬: 65, 68, 73, 83, 92, 90, 64, 68, 77, 76, 81.
ќтвет: √ипотеза 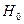 об отсутствии различий между выборками по уровню исследуемого признака отвергаетс€.
об отсутствии различий между выборками по уровню исследуемого признака отвергаетс€.
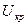 = 43,
= 43, 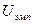 = 33.
= 33.
4). ѕрин€ть α = 0,01. ¬ыборка ј: 50, 60, 70, 80, 90, 100, 250, 350, 450, 550, 650, 750, 850, 900. ¬ыборка ¬: 50, 60, 70, 80, 90, 100, 200, 300, 400, 500, 500, 600, 600.
ќтвет: √ипотеза 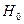 об отсутствии различий между выборками принимаетс€.
об отсутствии различий между выборками принимаетс€.
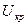 = 43,
= 43, 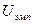 = 74,5.
= 74,5.
5). ѕрин€ть α = 0,05. ¬ыборка ј: 45, 42, 38, 38, 34, 33, 30, 28, 15, 14. ¬ыборка ¬: 45, 41, 38, 33, 31, 30, 21, 20, 20, 14.
ќтвет: √ипотеза 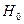 об отсутствии различий между выборками принимаетс€.
об отсутствии различий между выборками принимаетс€.
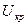 = 23,
= 23, 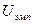 = 43.
= 43.
¬ыбор критери€ различий
ритерии, которые рассматривались в этой главе, предполагают, что сопоставл€ютс€ две независимые выборки. ѕри этом, если объем выборки  ,
, 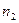 ≥ 11, то используют Q-критерий –озенбаума, если же
≥ 11, то используют Q-критерий –озенбаума, если же  или
или 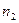 < 11, следует применить U-критерий ћанна-”итни.
< 11, следует применить U-критерий ћанна-”итни.






