Так как оба ограничения этой задачи активно, то товары обоих видов необходимо продавать. По второй теореме двойственности это означает, что остатков ресурсов не будет, и ограничения-неравенства двойственной модели превратятся в ограничения-равенства.
Решая соответствующую модель, находим стоимости ресурсов.
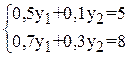
у1 = 8,75 ден. ед., у2 = 6,25 ден. ед.
Проверим выполнение первой теоремы двойственности.
Min Z’= 370*8,75+90*6,25=3800 ден. ед.
Это означает, что выручка от продажи товаров будет равна суммарным расходам на продажу товаров первого и второго вида.
Аналогично можно проверить выполнение рентабельность продаж изделий.
Для товара первого вида: 0,5*8,75+0,1*6,25=5 – следовательно, продавать товары первого вида рентабельно.
Для товара первого вида: 0,7*8,75+0,3*6,25=8 – следовательно, продавать товары второго вида рентабельно.
Этот же вывод можно сделать исходя из второй теоремы двойственности.
Построим матрицу взаимозаменяемости ресурсов.
| у1 | у2 | |
| у1 | 6,25/8,75=0,71 | |
| у2 | 1,4 |
Это означает, что одну единицу второго ресурса можно заменить 1,4 единицами первого ресурса.
Рассмотрим необходимость покупки двух единиц первого ресурса по цене 50 ден. ед. за партию и трех единиц второго ресурса по цене 15 ден. ед. за партию.
Так как одну единицу первого ресурса предлагают по цене 50/2=25 и это больше, чем 8,75, то покупка первого ресурса по таким ценам невыгодна, одну единицу второго ресурса предлагают по цене 15/3=5 и это меньше, чем 6,25, поэтому покупка второго ресурса по таким ценам выгодна.
Тем не менее, вопрос о покупке ресурсов невозможно рассматривать без учета устойчивости. Так как малейшее изменение условий задачи приведется к изменению оптимального плана продаж.
Для того чтобы определить устойчивость необходимо найти матрицу, обратную к матрице ограничений.
В данном случае это будет матрица 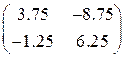
Найдем устойчивость по количеству ресурсов. Для нахождения на сколько можно уменьшить количество ресурсов из обратной матрицы берутся только положительные числа, соответственно для нахождения на сколько можно увеличить объем ресурсов из обратной матрицы берутся только отрицательные величины по модулю.
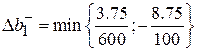 =0,00625
=0,00625
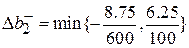 =0,0625
=0,0625
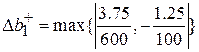 =0,0125
=0,0125
 =0,014583
=0,014583
Таким образом,
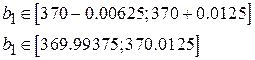 ,
, 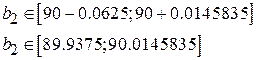
Для расчета по цене товара используется аналогичная методика.
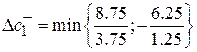 =2,33
=2,33
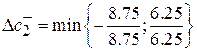 =1
=1
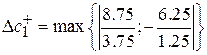 =5
=5
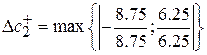 =1
=1
Таким образом, 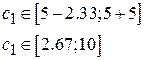 ,
, 
С помощью анализа решения можно ответить и на вопрос продажи нового продукта, если известны затраты ресурсов и продажная цена.
Например, если предлагается на продажу товар третьего вида по цене 10 ден. ед., который требует времени продавца в объеме 1,5 ед., и занимает площадь 0,5 ед., то затраты на его продажу составят 1,5*8,75+0,5*6,25=16,25 ден. ед. Это явно больше 10 ден. ед. прибыли, которой товар третьего типа мог бы принести, и его продажа на данных условиях не выгодна.






