Каждая задача линейного программирования, называемая прямой или исходной, тесно связана с другой задачей, ее называют двойственной.
Математические модели этих задач имеют следующий вид.
прямая задача:
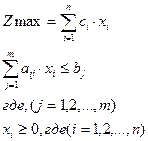
| двойственная задача:
|
Эти задачи экономически могут быть сформулированы следующим образом.
Прямая задача: сколько и какой продукции хi(i-1, 2, …, n) надо произвести, чтобы при заданных стоимостях единицы продукции Сi, объемом имеющихся ресурсов bj (j=1,2,…, m) и нормах расхода ресурсов аij максимизировать выпуск продукции в стоимостном виде.
Двойственная задача: какова должна быть оценка единицы каждого ресурса yj (j=1, 2,…, m), чтобы при заданных bj, ci и аij минимизировать общую оценку затрат на все ресурсы.
Правила построения двойственной задачи по имеемой прямой задаче:
1) Если прямая задача решается на максимум, то двойственная задача решается на минимум; если прямая задача решается на минимум то двойственная на максимум;
2) В задаче на максимум ограничения неравенства имеют вид – ≤, а в задаче на минимум – ³;
3) Каждому ограничению прямой задачи соответствует переменная двойственной задачи, в другой модели ограничению двойственной задачи соответствует переменная прямой задачи;
4) Матрица системы ограничений двойственной задачей получается из матрицы из матрицы систем ограничений прямой задачи транспонированием;
5) Свободные члены системы ограничений прямой задачи являются коэффициентами при соответствующих переменных целевой функции двойственной задачи и наоборот;
6) Если на переменную прямой задачи наложено условие неотрицательности, то соответствующее ограничение двойственной задачи записывается как ограничение-неравенство, в противном случае – как ограничение равенство;
7) Если какое либо ограничение прямой задачи записано как равенство, то на соответствующую переменную двойственной задачи условие неотрицательности не налагается.
Пример:
Прямая задача:
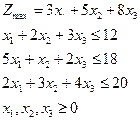
| Двойственная задача:
|
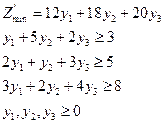
В этой задаче 
– предельные оценки стоимости единицы каждого ресурса, целевая функция – оценка стоимости всех ресурсов, а каждое ограничение есть условие, что оценка ресурсов, идущих на производство продукции 
, не менее чем цена единицы продукции.
Взаимосвязь решений прямой и двойственной задач находится из трех теорем двойственности.
3. 3 Теоремы двойственности.
Первая теорема двойственности:
Если одна из двойственных задач имеет оптимальное решение, то и другая задача имеет оптимальное решение, причем экстремальные значения целевых функций совпадают Z(X)=Z'(Y). Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.
Экономическое содержание первой теоремы двойственности: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения и оценок ресурсов, при этом полная стоимость продукта, полученного в результате реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадения, значений целевых функций для соответствующих решений пары двойственных задач достаточно для того, чтобы эти решения были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными только тогда, когда полная стоимость произведенной продукции и суммарная оценка ресурсов совпадает.
Оценки выступают как инструмент сбалансирования затрат и результатов. Двойственные оценки обладают тем свойством, что они гарантируют рентабельность оптимального плана, т.е. равенство общей стоимости продукции и ресурсов обуславливает убыточность всякого другого плана отличающегося от оптимального. Двойственные оценки позволяют сопоставлять и сбалансировать затраты и результаты производства.
Вторая теорема двойственности:
Для того чтобы план Х* и Y* пары двойственных задач были оптимальными, необходимо и достаточно выполнение условий:
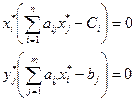
Эти условия называются условиями дополняющей нежесткости. Из них следует, что если какое-либо неравенство системы ограничений в одной из задач не обращается в строгое равенство оптимальным планом этой задачи, то соответствующий элемент оптимального плана двойственной задачи должен равняться нулю. Если какой-либо элемент оптимального плана одной из задач положителен, то соответствующее ограничение в двойственной задаче её оптимальным планом должно обращаться в строгое равенство, т.е.
если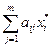 
< bj, то 
;
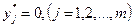если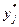 
> 0, то 
.
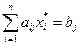Аналогично,
если 
> 
если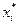 
>0 то 
Экономически это означает, что если по некоторому оптимальному плану X*=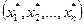 
производства расход j-го ресурса меньше его запаса bj, то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равна нулю. Если же в некотором оптимальном плане оценок его j-й элемент больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу. Отсюда следует вывод: двойственные оценки могут служить мерой дефицитности ресурсов. Дефицитный ресурс, т.е. полностью используемый по оптимальному плану производства, имеет положительную оценку, а избыточный ресурс, т.е. не используемый полностью имеет нулевую оценку.
Третья теорема двойственности:
Двойственные оценки показывают приращение функции цели, вызванное малым изменением свободного члена соответствующего ограничения задачи линейного программирования, т.е.
В последнем выражении дифференциалы заменим приращениями. Тогда получим выражение:
,
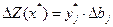если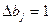 
, тогда 
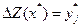, Экономическое содержание третьей теоремы двойственности: двойственная оценка численно равна изменению целевой функции при изменении соответствующего ресурса на единицу. Двойственные оценки yj часто называются скрытыми теневыми или маргинальными оценками ресурсов.
3.4 Решение задач линейного программирования
геометрическим методом
При решении задач линейного программирования геометрическим способом необходимо помнить, что визуализация решения достигается только при рассмотрении задачи с двумя переменными и небольшим количеством ограничений. Также желательно выбрать масштаб осей так, чтобы график был компактным, но было четко видно все точки пересечения ограничений.
С геометрической точки зрения в задаче линейного программирования ищется такая угловая точка или набор точек из допустимого множества решений, на которой достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.
Для нахождения экстремального значения целевой функции при графическом решении задач ЛП используют вектор gradZ на плоскости Х2ОХ2.
Этот вектор показывает направление наискорейшего изменения целевой функции. Координатами вектора grandZ являются коэффициенты целевой функции Z(x).
