Классификация решаемых экономических задач

По уровню информации о ситуации:

1. Деторминированный уровень – наиболее простой уровень информации о ситуации- когда условие, в которых принимаются решения, известны полностью.

2. Стохастический уровень – уровень, при котором известно множество возможных вариантов условий и их вероятностное распределение.

3. Неопределенный уровень - уровень, когда известно множество возможных вариантов, но без какой-либо информации об их вероятностях.

По виду информации о ситуации:

1. Статический вид – информация о ситуации не меняется во времени и известна заранее.

2. Динамический вид – информация о ситуации зависит от времени, прошедшего от начала операции.

По виду критерия оптимальности:

1.Однокритериальные задачи

2.Монокритериальные задачи

 

По типу критерия оптимальности:

1. Линейные задачи

2. Нелинейные задачи

 

По типу области ограничения:

1. Выпуклая область

2. Целочисленная область

3. Булева область

Контрольные вопросы.

6. Что означает понятие «экономическая модель»?

7. Классификация экономических моделей.

8. Классификация решаемых экономических задач.

9. Какое решение является оптимальным?

10. Дать определение показателя эффективности.

 

Лекция. Линейное программирование.

 

Общая постановка задачи

Линейное программирование — наука о ме­тодах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.

Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений.

 

Определение.

Математическое выражение целевой функ­ции и ее ограничений называется математической моделью экономической задачи.

В общем виде математическая модель задачи линейного программирования (ЛП) записывается как

 

Z(x)=C₁X₁+C₂X₂ + ^{. ..} +С_JX_J + ^... +С_nX_{n _} max(min)

при ограничениях:

 

 

где X_i — неизвестные;a _ij, b_j, C_i — заданные постоянные вели­чины.

 

Все или некоторые уравнения системы ограничений могут быть записаны в виде неравенств.

Математическая модель в более краткой записи имеет вид

Z(x) = ∑C_i X_i max(min)

при ограничениях:

 

 

Определение Допустимым решением (планом) зада­чи линейного программирования называется вектор X = (х₁, х₂,,...х_n,), удовлетворяющий системе ограничений.

 

Множество допустимых решений образует область допус­тимых решений (ОДР).

 

Определение Допустимое решение, при котором целевая функция достигает своего экстремального значения, называ­ется оптимальным решением задачи линейного программиро­вания и обозначается Х_опт.

Базисное допустимое решение

 

 

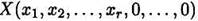
Является опорным решением, где r — ранг системы ограничений.