Построение на местности проектных высот

И линий заданного уклона

 

Часто от репера Государственной нивелирной сети невозможно передать высоту непосредственно на проектную точку. Для этого, как отмечалось выше, создают высотную геодезическую основу, которую закрепляют на строительной площадке. Саму высотную основу привязывают нивелирным ходом либо системами нивелирных ходов к исходным пунктам (реперам) геодезической сети.

Для выноса на местность проектной высоты используют, в основном, метод геометрического нивелирования, реже, при невозможности использовать указанный выше метод, - метод тригонометрического нивелирования.

Для выноса проектной высоты методом геометрического нивелирования нивелир устанавливают посредине между исходной и проектной точками (рис. 9.3). По исходной точке находят горизонт прибора

, (9.11)

где а – отсчёт по рейке, установленной на исходной точке.

 

Рис.9.3. Построение проектной высоты способом геометрического нивелирования.

 

Формулу (9.11) удобно использовать, если с данной станции выносят сразу несколько проектных высот.

Поскольку проектная высота Н_ПР известна, то известно и проектное превышение

, (9.12)

где b_ПР – отсчёт по рейке, установленной в проектной точке, соответствующий проектной высоте. Таким образом,

. (9.13)

Высотное положение проектной точки изменяют до тех пор, пока на рейке не установится отсчёт, равный b_ПР. После этого превышение h_ПР измеряют несколько раз (при нескольких горизонтах прибора) и убеждаются в обеспечении заданной точности построения высоты.

Проектная точка может быть подвижной по высоте, выполненной в виде болта (в конструкции), ею может быть деревянный или металлический кол, забиваемый в землю, часто на строительных конструкциях проектной точкой является черта (откраска) по основанию рейки.

При строительстве зданий всегда требуется передача проектной высоты (отметки) на другой монтажный горизонт, например, по колонне или стене. Для этого от проектной черты на стене или колонне нижнего горизонта рулеткой откладывают проектную разность двух монтажных горизонтов. При передаче высот на несколько монтажных горизонтов на каждом из них выполняют контрольное нивелирование по проектным отметкам.

 

 

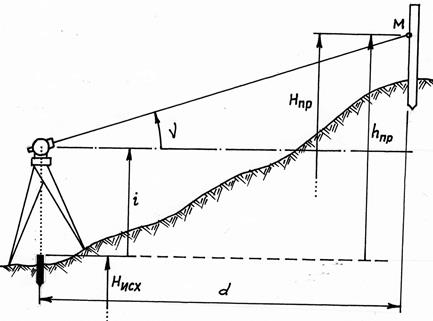
Рис.9.4. Построение проектной высоты способом тригонометрического нивелирования.

 

При использовании для построения проектной высоты метода тригонометрического нивелирования в исходной точке (в точке с известной высотой) устанавливают теодолит (рис. 9.4), измеряют его высоту i, горизонтальное проложение d и определяют угол наклона ν, соответствующий проектной высоте Н_ПР:

. (9.14)

Определяют отсчёт по вертикальному кругу теодолита при «круге право» и «круге лево», соответствующие значению полученного проектного угла наклона:

, (9.15)

где МО – место нуля, предварительно определенное на станции по 2-3 точкам.

Метка М будет соответствовать проектной высоте в заданной точке.

Для контроля построения проектной высоты следует изменить горизонт прибора, измерить несколькими приёмами угол наклона на метку М и вычислить значение проектной высоты по формуле:

(9.16)

Если при построении не будет обеспечена заданная точность, то метку М перемещают на величину расхождения в соответствующем направлении и выполняют контрольную проверку высоты.

Построение линии с проектным уклоном можно выполнить с помощью нивелира либо с помощью теодолита.

 

Рис. 9.5. Построение линии заданного уклона:

а) горизонтальным лучом; б) наклонным лучом нивелира; в) с помощью теодолита.

 

Геометрическое нивелирование удобно использовать при небольших проектных уклонах, например, при строительстве дорог. При значительных уклонах используют теодолит.

На рис. 9.5 представлена схема построения линии. Нивелир устанавливают в створе проектной линии в точке 1 (рис. 9.5 а), высота которой известна (Н_1(ПР)). Далее, на расстояниях d_i от точки 1, выставляют точки на их проектную высоту

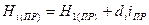(9.17)

с вычислением для каждой из них соответствующего отсчёта по рейке, как это выполнялось при передаче на точку проектной высоты.

В другой схеме (рис. 9.5 б) определяют проектную высоту в конечной точке 2 линии и элевационным винтом нивелира добиваются совпадения отсчётов а по рейкам, установленным в точках 1 и 2. Далее, в промежуточных точках по створу линии выставляют точки, на которых отсчёт по рейке также должен быть равным отсчёту а.

Во второй схеме вместо нивелира можно использовать теодолит (рис. 9.5 в). Теодолит устанавливают в проектной точке 1, определяют проектный угол наклона

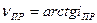, (9.18)

по нескольким измерениям определяют место нуля вертикального круга и вычисляют по формулам (9.15) отсчёт по вертикальному кругу, соответствующий проектному углу. При полученном отсчёте визируют на точку 2 проектной линии и по рейке, установленной в этой точке, берут отсчёт а. Для промежуточных точек линии должны также обеспечиваться такие же отсчёты по рейкам.

 

 

Рис. 9.6. Построение проектного уклона с помощью визирок.

 

После построения линии с заданным уклоном необходимо выполнить контрольные измерения по её зафиксированным на местности точкам и убедиться в правильности построения, т.е. в обеспечении необходимой точности построения проектного уклона. Целесообразно контрольные измерения выполнять способом геометрического нивелирования, если это возможно по условиям измерений.

 

Пример 9.3. Построение проектного уклона с помощью теодолита.

Исходные данные.

Величина проектного уклона i_ПР =-0,145. Точность построения уклона Место нуля МО = -0⁰02,4'. Горизонтальное проложение линии 1-2 d₁₂ = 65,356 м. Проектная высота в точке 1 Н_1(ПР) = 156,857 м.

Решение.

Определяем проектную высоту в точке 2:

Н_2(ПР) = Н_1(ПР) + d₁₂i_ПР = 156,857 + 65,356(-0,145) = 147,380 м.

По формулам (9.18) и (9.15) находим значения проектного угла и отсчётов по вертикальному кругу при «круге лево» и «круге право»: ν_ПР = -8⁰15,0'; ВК(КЛ) = -8⁰15,0' + +(-0⁰02,4') = -8⁰17,4'; ВК(КП) = -0⁰02,4'- (-8⁰15,0') = +8⁰12,6'.

Отсчёт по рейке в точке 2 при наблюдениях после установки отсчётов по вертикальному кругу при положениях КЛ и КП составил а₂ = 1476 мм.

При контрольном нивелировании максимальное расхождение в проектных высотах по линии 1-2 на расстояниях 15 м составило 15 мм. Таким образом, погрешность в построении проектного уклона составила 15 мм/15000 мм = 0,001, что удовлетворяет поставленной задаче.

 

При выполнении аналогичных работ, не требующих высокой точности, можно пользоваться тремя визирками одинаковой длины (рис. 9.6), которые представляют собой вертикальный брусок с прикреплённой к нему горизонтальной планкой.

Две визирки устанавливают в точках 1 и 2 с предварительно выставленными на них проектными высотами. Третью визирку перемещают по створу линии 1-2 и «на глаз» совмещают горизонтальные планки всех трёх визирок (наблюдатель должен находиться в точках 1 или 2). По основанию третьей визирки фиксируют точку с её проектной высотой, соответствующей заданному проектному уклону.

 

Способы разбивочных работ

 

Способ прямой и обратной угловых засечек. Чаще всего эти способы применяют для выноса недоступных точек, а также точек, находящихся на значительных расстояниях от геодезической основы.

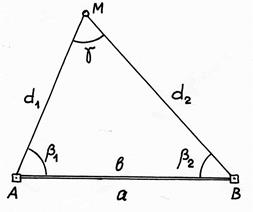
В способе прямой угловой засечки (рис. 9.7 а) положение точки М определяют с исходных пунктов А и В геодезической основы построением в каждой из них горизонтальных углов β₁ и β₂, которые являются разбивочными элементами. Указанные углы строят на местности по правилам, изложенным в § 88. В данной схеме целесообразно использовать одновременно два теодолита. При этом положение проектной точки фиксируют по команде двух наблюдателей при положениях КЛ, а затем – при положениях КП. После фиксирования среднего положения точки М выполняют контрольное измерений углов β₁ и β₂.

Необходимо иметь в виду, что величина угла γ при точке М не должна быть малой и слишком большой. Оптимальным углом, при котором вынос точки может быть выполнен с меньшей погрешностью, является при примерно равных расстояниях от исходных точек до точки М. То есть следует стремиться обеспечить симметричную схему построения точки М. Кроме того, для повышения точности построения проектной точки, а также для контроля её построения, вынос проектной точки на местность выполняют часто с двух базисов геодезической разбивочной основы.

Во многих случаях бывает сложно из одного приема вынести точку М с заданной точностью в её проектное положение. В таких случаях используют способ замкнутого треугольника. Вынос точки осуществляют последовательными приближениями. Для этого с максимально возможной точностью выполняют построение точки М, затем несколькими приёмами измеряют все углы треугольника, уравнивают углы и вычисляют координаты точки М из решения по формулам прямой угловой засечки. Полученные координаты сравнивают с проектными и при недопустимых отклонениях в их значениях определяют поправки (редукции) в положение точки М и смещают последнюю в проектное положение. Для контроля снова измеряют углы и выполняют аналогичные вычисления.

 

 

Рис. 9.7. Вынос проектной точки способами прямой и обратной угловых засечек:

а) способ прямой угловой засечки; б) способ обратной угловой засечки.

 

Рис. 9.8. Вынос на местность проектной точки способом полярных координат.

Рис. 9.9. Вынос на местность проектной точки способом проектного полигона.

Мотод последовательных приближений используют и в способе обратной угловой засечки (рис. 9.7 б). Предварительно точку М выносят на местность и измеряют при ней углы β₁ и β₂. По формулам обратной угловой засечки определяют координаты точки М и сравнивают их с проектными. При необходимости положение точки М редуцируют на величины отклонений по координатам Х и Y, точку М фиксируют в положении М₂ и снова уже в новой точке измеряют горизонтальные углы β а затем вычисляют координаты новой точки М. Все указанные действия выполняют до тех пор, пока задача качественного построения проектной точки не будет решена.

Способ полярных координат используют в тех случаях, когда проектные точки находятся сравнительно недалеко от точек геодезической основы. При этом предпочтительно, чтобы расстояния до них не превышали длины мерного прибора (ленты или рулетки).

На местности от исходного направления АВ (рис. 9.8) строят проектный угол β и проектное расстояние d, которые в данном способе являются разбивочными элементами.

Проектная точка может находиться далеко от точек геодезической основы или не может быть вынесена по техническим условиям способами угловой засечки. В таких случаях к точке прокладывают полигонометрический ход (рис. 9.9), используя для этого последовательно расчётные проектные углы и проектные расстояния. Данный способ называют способом проектного полигона.

По двум ходам от базисной линии АВ геодезической основы получают два положения точки М из решения ходов (1) и (2). В качестве первого приближения вычисляют средние значения координат проектной точки. Затем в полученной точке М измеряют угол β_М и линии d₃ и d₄ и вычисляют координаты точки М в общей схеме замкнутого полигона. Если координаты точки М будут значительно отличаться от проектных, то определяют поправки (редукции) в положение точки М, точку смещают и снова измеряют угол β_М и линии d₃ и d₄. Из решения хода находят координаты точки М и сравнивают их с проектными. Такие действия выполняют до достижения необходимой точности построения проектной точки.

 

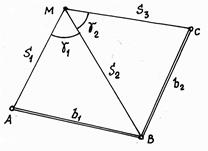Рис. 9.10. Вынос на местность проектной точки способом линейной засечки.

Рис. 9.11. Способы створных засечек: а) способ створно-линейной засечки; б) способ створной засечки.

 

При небольших расстояниях от проектной точки до точек геодезической основы удобно использовать способ линейной засечки, реализуемый с помощью двух или трёх рулеток (рис. 9.10). Разбивочными элементами в этом способе являются только расстояния S или горизонтальные проложения.

Для выноса осей сооружений удобно использовать способы створных засечек (рис. 9.11).

В схеме створно-линейной засечки (рис. 9.11 а) положение точки М определяют на линии створа, образованного пунктами А и В геодезической основы. По линии створа проектным расстоянием d задают положение искомой точки М. При необходимости положение точки М может быть проконтролировано с другой точки створа. В точке А створа устанавливают теодолит, а в точке В – визирную цель (на штативе, с возможностью центрирования и горизонтирования).

В схеме створной засечки (рис. 9.11 б) точку М задают на линии пересечения створов АВ и СD. Для повышения точности работу целесообразно выполнять одновременно двумя теодолитами и двумя визирными целями несколькими приёмами с перестановкой теодолитов и визирных целей. Для контроля измеряют расстояния от построенной точки до исходных пунктов геодезической основы.

Обычно на строительной площадке имеется т.н. строительная сетка. В её системе координат задано положение всех осей (главных, основных и т.д.), а также всех главных (узловых) точек. В этом случае вынос проектных точек осуществляется в системе координат строительной сетки по приращениям координат Δ x и Δ y (рис. 9.12). В общегосударственной или местной системах координат ХОY используется система координат хАy строительной сетки c началом координат в точке А. Ось Аy задается исходным направлением на другую исходную точку (В) геодезической основы. Положение точки М определяется расстояниями Δ x и Δ y, т.е. приращениями координат в системе координат строительной сетки.

Рис. 9.12. Разбивка точек сооружения от строительной сетки.	Рис. 9.13. Способ бокового нивелирования.

Предварительно строят проектное расстояние Δ y, устанавливают в полученной точке С теодолит, строят проектный угол β, равный 90⁰ на точку М и в полученном направлении откладывают отрезок Δ x. Для обеспечения более высокой точности построения точки меньшее из Δ x и Δ y следует строить в виде перпендикуляра, а большее – по створу исходной линии.

Вынос вертикальных осей конструкций выполняют способом бокового нивелирования (рис. 9.13). От оси АВ, на которой находится строительная конструкция, например, колонна, а небольшом расстоянии l строят линию А'В', параллельную исходной линии АВ. В точке А' устанавливают теодолит, который визируют на марку, находящуюся в точке В'. Перпендикулярно к оси колоны последовательно на её основание и верх устанавливают рейку Р (с уровнем, ориентированным осью по продольной оси рейки) и берут отсчёты а₁ и а₂ по вертикальной нити сетки зрительной трубы. Равенство указанных отсчётов определяет вертикальность оси колонны. Если расхождение между отсчётами недопустимо, то положение вертикальной оси колонны выправляют.