Автор возвращает Вас к разделу о разбивке главных точек кривой на трассе линейного сооружения (см. §63). Там говорилось о действиях на местности, которые не могли ещё восприниматься Вами, как понятные по их содержанию и исполнению. Например, привязка трассы. Теперь у вас с этим нет никаких проблем: есть съёмочное обоснование в виде теодолитного хода, есть заданное направление трассы, есть проектное положение нулевого пикета (ПК0). Остаётся только вычислить разбивочные элементы и построить положение ПК0 и направление ПК0-ПК1 на местности. То и другое Вы уже знаете как делать. Или, например, вот эта фраза «теодолитом откладывают угол…» теперь никак Вас не смутит, поскольку об этом как раз вы только что читали в §88 (о построении на местности проектного горизонтального угла). Да и вообще, дальше, Вам будет всё легче и легче, поскольку комплекс геодезических работ тесно взаимосвязан с теми методами и приёмами их исполнения, которые были раньше рассмотрены в предыдущих главах.
В главе 6 были рассмотрены вопросы нивелирования трассы, например, при строительстве дороги. Перед выполнением нивелирования производят разбивку пикетажа, для чего используется теодолит и мерный прибор (дальномер, светодальномер, рулетка) либо только электронный тахеометр.
Для задания направления трассы от какого-либо исходного направления вычисляют проектное значение угла β и строят этот угол на местности, т.е. задают начальное направление трассы от пикета ПК0) до первого угла её поворота УП (рис. 9.15). Автор только что об этом и говорил.
Расстояние между пикетами соответствует 100 м в горизонтальном проложении (либо другому установленному расстоянию, например, 50 м). В связи с тем, что местность может иметь наклон к плоскости горизонта, в проектное расстояние вводят поправку за наклон. При перегибах местности между пикетами (например, между пикетами ПК2 и ПК3) поправки за наклон вводят для каждого из наклонных отрезков с учётом углов наклона ν1 и ν2.
По мере удаления трассы от пикета ПК0) створ линии задают теодолитом, последовательно перемещая его на другие пикеты, с визированием на удаленный задний пикет отсчётом по горизонтальному кругу 0о. В этом случае продолжение створа будет соответствовать отсчёту по горизонтальному кругу 180о.
В точке угла поворота УП выполняют разбивку кривой заданного радиуса. Основные элементы кривой вычисляют по формулам (6.25) – (6.29).
В процессе разбивки кривой все пикеты за углом поворота следует переместить вперёд на величину домера (Д), поскольку длина кривой меньше двух её тангенсов (Т).
Детальная разбивка кривой может выполняться несколькими способами (рис. 9.16).
При разбивке кривой по частям (рис. 9.16 а) всю её, от начала кривой (НК) до конца кривой (КК), делят на две одинаковые кривые: НК-М и М-КК. Для каждой из них производят детальную разбивку, принимая значения НК1' = 1'2 = 23' = 3'КК = Т. При этом значение Т вычисляют по формуле
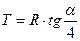. (9.23)
Точки 1' и 3' находятся на линиях НК-УП и КК-УП.
После построения точек 1' и 3' каждую из кривой разбивают способом координат (рис. 9.16 б).
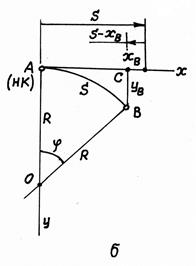
В способе координат положение любой из точек кривой получают в условной системе прямоугольных координат хоy. Ось y – направление от начала кривой к её центру 0; ось х – направление тангенса (Т), т.е. касательной в точке начала кривой.
Координаты точки В, которая находится на расстоянии s, будут равны
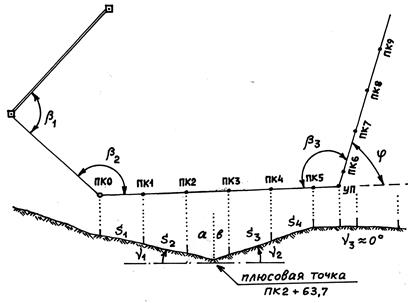
Рис. 9.15. Разбивочные работы при трассировании линейных сооружений.
| 
|
|
|
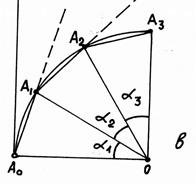
Рис. 9.16. Детальная разбивка кривых на трассе:
а) разбивка кривой по частям; б) способ координат; в) способ хорд; г) способ углов.
; 
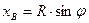, (9.24)
где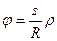 
; ρ- радиан.
При радиусах до 500 м разбивку кривой ведут через 10 м, а при б о льших радиусах – через 20 м.
Технология разбивки следующая. От точки А рулеткой по направлению тангенса, задаваемому теодолитом, откладывают отрезок s. Находят разность (s – x) и откладывают её в обратном направлении. В полученной точке устанавливают теодолит и строят им (и Вы знаете, как это делается!) угол 90о от направления тангенса (линия СВ). Затем по направлению СВ откладывают координату у.
Схема разбивки кривых способом хорд (продолженных или последовательных) представлена на рис. 9.16 в).
При детальной разбивке кривой отрезки (хорды) АоА1 = А1А2 = А2А3 = а. Вообще говоря, значение а может быть и произвольным, но не более длины имеющейся рулетки. Для точки А1
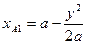, (9.25)
или
, (9.26)
где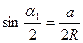 
.
Точки К1 и К2 и т.д. на кривой можно построить способом линейной засечки. По линии АоВо следует отложить хорду а до точки В1, а затем из неё отрезком 0,5 s и из точки Ао отрезком а получить положение точки К1. В этом случае 
.
Чтобы построить точку А2 продолжают линию АоА1 на расстояние а (А1А 2 = а). Из точки А1 радиусом а и из точки А2' радиусом s засекают положение точки А2. Последующие точки получают аналогично.
При детальной разбивке способом углов (рис. 9.16 г) на кривой получают равноотстоящие друг от друга точки А1, А2, …, как и в способе хорд. Для этого в точке Ао устанавливают теодолит и ориентируют 0о горизонтального круга по направлению АоВо (по линии тангенса). Затем устанавливают по горизонтальному кругу отсчёт 0,5 α1 и в этом направлении откладывают хорду а (в точке А1). Далее снова по горизонтальному кругу устанавливают отсчёт 2(0,5 α1), один конец рулетки фиксируют в точке А1, а другой её конец на отсчёте а совмещают в изображении через зрительную трубу теодолита с вертикальной нитью (точка А2) по команде наблюдателя. По аналогии с точкой А2 достраиваются остальные точки, изменяя каждый раз отсчёт по горизонтальному кругу на 0,5 α1. Такие же действия выполняют и из точки КК конца кривой.
Способ стягивающей хорды (рис. 9.17) используют обычно в тех случаях, когда радиус кривой слишком большой, а также в тех случаях, когда нет доступа к центру кривой. Этот же способ используют и для построения переходных кривых.
Рис. 9.17. Способ стягивающей хорды.
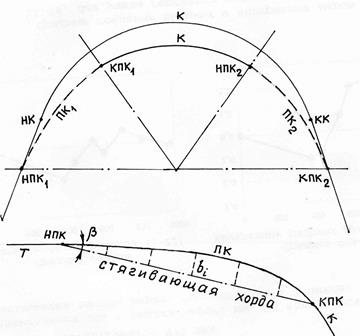
Рис. 9.18. Переходная кривая.
При разбивке круговых кривых разбивочные работы выполняют по частям, короткими хордами либо длинными хордами, но с учётом уклонения кривой от хорды. Если задаться значением угла φ, то можно определить длину хорды
, (9.27)
а величину стрелки прогиба bo в середине кривой – по формуле
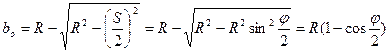(9.28)
Величины стрелок прогиба bi получают по приближённой формуле:
(9.29)
через шаг в 2 м по обе стороны от стрелки bo. Поскольку круговая кривая симметричная, то величины рабочих промеров от середины кривой при равных шагах разбивки по обе стороны будут одинаковыми.
Переходные кривые выполняют в местах сопряжения круговых кривых с прямолинейными участками железных дорог с целью ослабления резких ударов на поворотах при больших скоростях от действия центробежной силы. Для этого в местах сопряжений делают вставку (рис. 9.18), радиус которой изменяется от бесконечности (на прямой) до радиуса круговой кривой. После перехода через круговую кривую радиус изменяется соответственно от радиуса кривой до бесконечности.
Чаще всего для переходных кривых используют радиальную кривую (спираль), уравнение которой имеет вид
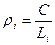, (9.30)
где С – параметр кривой (постоянный коэффициент; его выбирают в пределах 45000 – 150000 в зависимости от скорости движения поезда; при небольших скоростях С < 45000); Li – длина переходной кривой до точки i; ρi – радиус кривизны кривой в указанной точке.
Значения стрелок прогиба через определенный шаг вычисляют от стягивающей хорды с учётом параметров переходной кривой. Поскольку переходная кривая несимметричная, то величины стрелок прогиба будут различными, т.е. разбивку следует выполнять нарастающим итогом либо от НПК (начала переходной кривой), либо от её конца (КПК). Для определения стрелок прогиба переходных кривых существуют специальные таблицы.
Способ стягивающей хорды является более точным из всех, рассмотренных выше, поскольку значения промеров bi значительно меньше, чем промеры от тангенса.
