В абсолютном большинстве случаев в геодезических работах производят двукратные измерения однородных величин: длин линий (примерно одинаковых по величине), горизонтальных углов (образованных примерно одинаковыми по величине сторонами), превышений и др. Также, как и при многократных измерениях одной величины, здесь возникает необходимость оценки точности измерений, т.е. определения СКП разности двойных измерений.
Предположим, что мы имеем ряд из n парных равноточных измерений хi и xi´, для которых можно составить разности di:
di = xi - xi´. (3.36)
В этом случае, полагая, что в исследуемом ряду в разностях не содержатся систематические погрешности, можно записать для СКП разности
. (3.37)
Поскольку измерения равноточные, то можно записать, что
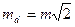, (3.38)
где m – СКП одного измерения.
С учетом (3.37) и (3.38) получим
. (3.39)
Двойные измерения одной величины позволяют в большой степени обнаружить систематические погрешности одного знака и примерно одной величины (односторонние погрешности). Если систематические погрешности отсутствуют, то сумма разностей двойных измерений весьма близка к нулю, т.е. [ d ] = 0. Наличие в измерениях систематической погрешности приводит к её накоплению в сумме разностей двойных измерений, в связи с чем получится величина Q = [ d ]. При n измерениях доля накопленной систематической погрешности в каждой разности будет составлять
. (3.40)
Если из значений разностей двойных измерений исключить величину систематической погрешности,
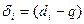, (3.41)
то СКП разности можно вычислить по формуле
, (3.42)
а СКП одного измерения – по формуле
. (3.43)
Пример 3.9. В табл. 3.6 приведена обработка результатов двойных равноточных однородных измерений длин линий светодальномером. Требуется определить наличие в результатах измерений систематической погрешности и выполнить оценку точности одного измерения.
Решение.
Разности d в таблице получены как 1-е измерение минус 2-е измерение.
Сумма разностей двойных измерений [ d ] = - 0,046 м, что говорит о наличии в результатах двойных измерений систематической погрешности. Её значение равно qi = [ d ] / n = = -0,046: 9 = -0,005 м.
Образуем ряд случайных погрешностей, см. формулу (3.34), и возведём полученные уклонения в квадрат (для сокращения записи введён сомножитель 10-6).
Сумма квадратов уклонений [ δi2 ] = 237 · 10-6 = 0,000237.
СКП разности двойных измерений
м.
СКП одного измерения m = md / 
= 0,0054 / 1,41= 0,004 м.
Таблица 3.6
К примеру 3.9
| №№ п/п | 1-е измерение, хi, м | 2-е измерение, хi´, м | Разности, di, м | Система-тическая погрешность, qi | Случайная погрешность, δi | δi2∙ 10-6 |
| 647,263 | 647,261 | + 0,002 | - 0,005 | + 0,007 | ||
| 624,850 | 624,857 | - 0,007 | - 0,005 | - 0,002 | ||
| 636,304 | 636,315 | - 0,011 | - 0,005 | - 0,006 | ||
| 652,842 | 652,844 | - 0,002 | - 0,005 | + 0,003 | ||
| 638,219 | 638,209 | - 0,010 | - 0,005 | - 0,005 | ||
| 625,347 | 625,346 | + 0,001 | - 0,005 | + 0,006 | ||
| 644,936 | 644,936 | 0,000 | - 0,005 | + 0,005 | ||
| 650,027 | 650,015 | - 0,012 | - 0,005 | - 0,007 | ||
| 641,006 | 641,013 | - 0,007 | - 0,005 | - 0,002 |
Следует иметь в виду, что значение m получено как вероятная погрешность по девяти парным измерениям сравнительно одинаковых длин линий. Случайные погрешности в измерениях 1, 3, 6 и 8 превышают полученное значение md. Независимо от этого принято считать, что любая из линий измерена со средней квадратической погрешностью 0,004 м.
Среднее значение любой измеренной линии имеет погрешность М = 
= 0,003 м, как это следует из формулы (3.21) для двух измерений.
