До сих пор мы говорили о результатах измерений, точность которых (степень доверия к ним) была одинаковая, весьма близкая по величине. Строго говоря, в практике измерений не существует равноточных величин. Обеспечить это весьма сложно, да во многих случаях и нет в этом необходимости. К равноточным измерениям можно отнести все результаты, погрешности которых не выходят за пределы допустимой величины, например, двойной СКП.
Часто приходится иметь дело с разнородными величинами. Например, при выполнении геодезических измерений использовать результаты длин линий, которые значительно отличаются по величине либо измерены разными по точности приборами, либо однородные величины в группе измерены равноточно, но с разным числом измерений в группах и т.п. В этом случае, при оценке точности, говорят о неравноточных измерениях.
Перед Вами появляется почти новое для Вас слово – вес. Да нет, слово вес для Вас хорошо знакомо, но вес измерения – это совсем не тяжёлое расстояние или тяжёлый горизонтальный угол. Хотя при измерениях то и другое могут достаться не совсем легко. Смысл веса можно пояснить следующей фразой: «Его слова имеют большой вес». Это значит, что этому человеку можно доверять, и сказанное им является неоспоримым или хотя бы важным в данной ситуации.
А что же может явиться мерилом важности того или иного результата измерения? Как установить, какой из этих результатов «весомее»? Подходов к решению такой задачи много.
Пусть, например, мы измерили одно и то же расстояние S двумя светодальномерами, А и В, имеющими соответственно паспортную точность измерений, равную 5 и 10 мм. Получены следующие результаты: SA = 1826,532 м и SB = 1826,541 м. Очевидно, что мы просто обязаны больше доверять результату SA = 1826,532 м, чем другому. В данном случае только лишь потому, что он получен с использованием прибора, имеющего б о льшую точность.
Здесь, если обозначить точность каждого прибора как mA и mB, мы можем получить относительную характеристику
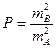, (3.44)
которая и называется весом. Весом результата SA по отношению к результату SB как степенью доверия этого результата по отношению к другому.
Таким образом, если в качестве веса результата измерения взять число, которое характеризует точность, то по смыслу слова вес можно сказать, что, чем больше вес результата, тем выше его точность (тем меньше погрешность, с которой получен данный результат). То есть вес находится в обратно пропорциональной зависимости от погрешности результата.
Пусть точность измерения какой-либо величины характеризуется СКП m, тогда вес Р определяют как отношение
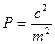. (3.45)
Значение с может быть любым, кроме нуля, но для анализируемой группы результатов измерений его принимают равным примерно среднему значению m по группе, поэтому значения весов результатов измерений не будут слишком большими или слишком маленькими.
В случае, когда mA = mB, вес равен единице – результаты измерений являются равноточными.
Очевидно, что величина СКП зависит от числа измерений, а это значит, что от числа измерений зависит и вес: чем б о льшим числом измерений получен тот или иной результат, тем больше его вес.
Рассмотрим следующий случай. Пусть результат SA1 = 652,345 м был получен прибором А, как среднее арифметическое из nA1 = 6 измерений. Затем тем же прибором А было измерено то же расстояние, но выполнено было nA2 = 9 измерений (получился результат SA2 = 652,348 м). Если возвратиться к формулам (3.21) или (3.22) определения средней квадратической ошибки среднего арифметического, то мы увидим, что эта погрешность зависит от числа измерений: чем больше число измерений, тем меньше погрешность. В данном случае можно полагать, что mA1 > mА2. А это значит, что отношение
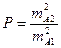(3.46)
будет меньше единицы. То есть результаты измерений оказались неравноточными, несмотря на то, что они были получены при использовании одного и того же прибора. Большее доверие здесь результату, полученному при большем числе измерений.
Уже при обработке ряда равноточных измерений мы сталкивались с результатами, имеющими разный вес. Если принять за единичный вес результат одного измерения, то среднее арифметическое будет получено с б о льшим весом, причем вес его будет в n раз больше, чем вес результата одного измерения.
Предположим, что при равноточных измерениях одной и той же величины Х (заранее неизвестной) выполнено три серии по ni наблюдений в каждой: n1, n2, n3, причем n1> n2> n3. Примем значение с2 (с → no = n1) в формуле (3.45) равным n1. Поскольку значение СКП обратно пропорционально корню квадратному из числа измерений, то квадрат СКП будет обратно пропорционален числу измерений. В связи с этим формулу (3.45) можно переписать в виде
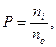(3.47)
В рассматриваемом случае Р1 = 1, Р2 = n2 /n1, Р3 = n3 /n1. Это говорит о том, что серии измерений неравноточны между собой.
Обозначим результаты измерений в сериях 1, 2 и 3 как x1i, x2i, x3i и
вычислим средние арифметические значения измеренной величины в каждой из серий: x1о, x2о и x3о по формуле (3.7).
Для всей группы измерений значение арифметической середины xо определится с учётом их весов из выражения
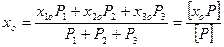. (3.48)
Аналогичная формула получится и для случая n серий измерений.
Из формулы (3.48) следует, что вес арифметической середины равен сумме весов всех измерений, входящих в серии.
Веса всех измерений можно изменить в одинаковое число раз. От этого значение арифметической середины не изменится. То есть в качестве no можно взять и другое число, отличное от n1, n2 и n3. Это число (с, no и др.) называют единицей веса.
Для оценки весов неравноточных измерений или групп неравноточных измерений используют различные приёмы. Так, если известны средние квадратические погрешности в группах измерений, то в качестве единицы веса, обозначим ее буквой μ, может быть выбрана любая из известных СКП либо примерно среднее её значение. Вес результата измерения в группе в этом случае определится по формуле (3.45)
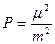. (3.49)
В некоторых случаях в качестве единицы веса используют число измерений в группе. Даже если предположить, что каждая из величин в каждой из групп измеряется равноточно, то при разных числах измерений в группе образуются результаты средних арифметических, неравноточных между собой. Здесь приемлемо использовать для вычисления весов формулу (3.46).
В качестве единицы веса может выступать и, например, измеряемое расстояние, если погрешность его определения функционально зависит от его величины (практически это часто и имеет место). В зависимости от вида указанной функции единицей веса может быть непосредственно длина линии в первой степени либо в квадрате:
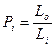; (3.50)
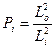, (3.51)
где Lo – единица веса измеряемого расстояния; Li – измеренное расстояние.
При измерении горизонтальных углов на местности в некоторых случаях в качестве единицы веса направления (отсчета по горизонтальному кругу теодолита – углоизмерительного геодезического прибора) используют величину этого направления, поскольку погрешность направления зависит от погрешности установки оси теодолита над вершиной измеряемого угла (погрешность центрирования). Чем короче расстояние (сторона угла), тем больше погрешность направления (обратная пропорциональная зависимость). В этом случае в качестве единицы веса при вычислении весов направлений целесообразно брать квадрат длины стороны.
При измерениях в линейно-угловых геодезических построениях, в тех случаях, когда выполняется уравнивание результатов измерений (см. главу 15), при обработке результатов измерений участвуют неоднородные величины, например, горизонтальные углы и расстояния. В таких случаях принято вес результата измерения расстояния оценивать по следующей формуле:
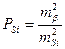, (3.52)
где mβ – СКП измерения горизонтального угла; mS – СКП измерения расстояния.
При использовании формулы (3.52) часто вес измеряемых горизонтальных углов принимают равным единице.
