«Жил на свете человек,
скрюченные ножки…».
Из детской книжки стихов.
В этом стишке не только ножки скрюченные. Всё там скрючено и кривенько. Да и не только там. Утром, идя на работу, учёбу, или вечером, приближаясь к дому, мы никак не ощущаем кривизны Земли (тоже, как выяснено, кривенькая). Больше нам мешают всякие кривые неровности на нашем пути. Поэтому кривизна Земли в некоторой степени вещь относительная.
При выполнении геодезических работ на сравнительно небольших территориях поверхность Земли можно принимать за плоскую, и измеренные расстояния на плоском изображении принимать равными соответствующим расстояниям на сферической поверхности. Чаще всего и приходится выполнять именно такие работы, на небольших по размерам территориях: в пределах площадки строительства, в пределах шахтного поля и т.п. При измерениях значительных по величине расстояний необходимо учитывать влияние кривизны поверхности Земли. Но, как будет показано дальше, измерение некоторых расстояний требует учёта кривизны Земли и для сравнительно небольших расстояний на её поверхности.
Для простоты изложения примем, что Земля представляет собой шар радиусом R (радиус Земли, представляемой в виде шара, принимают равным 6371,11 км). Предположим, что по поверхности шара из точки А в точку В перемещается (перекатывается) материальная точка (рис. 2.1), при этом расстояние S = АВ, которое пройдёт эта точка по поверхности шара, равно
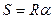, (2.1)
где α - центральный угол дуги АВ (в радианах).
Предположим, что точка движется по касательной в точке А к поверхности шара и пройдёт по ней путь Sо = AB', соответствующий движению по поверхности шара на пути S. Для величины So можно записать:
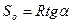. (2.2)
Разность в пройденных путях ΔS = (Sо - S) = R (tgα – α) и будет являться ошибкой в измеренном расстоянии из-за кривизны Земли.
Для малых значений углов α при разложении в ряд функции tg α получим
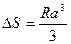, (2.3)
а после подстановки в выражение для S -
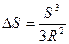, (2.4)
поскольку α = S / R.
Аналогично рассмотрим влияние кривизны Земли на определение вертикальных расстояний.
Математически установлено, что погрешнсоть (отклонение) h, равная разности отрезков ОВ' и OВ = R, находится через принятые ранее параметры по формуле
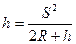
(2.5)
или, ввиду малой разности S и S о при малых α и h, - по формуле
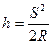. (2.6)
| Рис. 2.1. Учет влияния кривизны Земли. |
Оценка возможных погрешнсотей при измерении вертикальных и горизонтальных расстояний приведена в табл. 2.1.
Таблица 2.1
Погрешности в измеренных расстояниях из-за кривизны Земли
| Измеренное расстояние S, км | 0,1 | |||||||
| Абсолютная погрешность S, м | - | - | - | 0,001 | 0,008 | 1,03 | 8,2 | 65,7 |
| Относительная погрешность ΔS/S | 1/1250000 | 1/50000 | 1/25000 | 1/3000 | ||||
| Абсолютная погрешность h, м | 0,001 | 0,078 | 0,314 | 1,96 | 7,8 |
Точность измерения линий в геодезических сетях высших классов определяется относительной погрешностью порядка 1:400000, что практически является соизмеримым для S = 10 км (и, конечно, более 10 км). До 10 км при измерении горизонтальных расстояний во многих случаях влиянием кривизны Земли можно пренебречь.
Автор приностит свои извинения, что вводит в рассказ понятие относительная погрешнсоть, да и абсолютная погрешнсоть, без всяких необходимых пояснений этого понятия. Получается понятие без понятия. Но дальше об этом будет сказано несколько подробнее, а сейчас автор, думается, правильно посчитал, что читателю понятно слово погрешнсоть даже без определения этого слова. Ну а относительная погрешность – это та же погрешность, но выраженная просто в другой форме. Например, если абсолютную погрешность 8 мм разделить на измеренное расстояние 10 км (см. табл. 2.1), то как раз и получится вот такая относительная погрешность: 1/1250000.
Совсем другая картина наблюдается при оценке погрешностей в вертикальных отрезках. Как раз об этом и было предупреждение выше. Точность определения высот при геодезических работах, например, при топографической съёмке, определяется величиной 5 см, т.е. уже для расстояний S = 1000 м необходимо учитывать кривизну Земли. Если же точность измерений выше, например 5 мм и меньше, то учёт кривизны Земли следует начинать примерно для расстояний 250 – 300 м, что легко проверить обратным расчетом по формуле (2.6).
