Решение некоторых задач с использованием топографической карты

В данном разделе будут приведены описания игр с топографическими картами. Они не азартные, но весьма важные в работе геодезиста и маркшейдера, поскольку картографические материалы, выполненные на любых носителях (на бумаге, в электронном виде), являются практически единственным подспорьем для решения многих практических задач. В круг этих задач входит измерение расстояний, направлений, определение площадей, объёмов и мн.др.

 

17.1. Измерение расстояний

Использование численного, именованного и линейного масштабов. Положение любой точки земной поверхности на плоскости получается в результате проектирования её по определённым математическим законам на вспомогательную поверхность референц-эллипсоида и последующего построения плоского изображения в проекции Гаусса-Крюгера. При построении топографических планов выполняют ортогональное проектирование точек на горизонтальную плоскость. Очевидно, что расстояние между двумя точками, пройденное на местности, в общем случае отличается от его проекции на горизонтальную плоскость (рис. 2.30).

Даже и не в общем случае, а практически всегда, потому что невозможно представить себе какое-либо расстояние на поверхности Земли, равное его проекции на плоскость. Раньше говорилось, что в прокции Гаусса-Крюгера без искажений изображается осевой меридиан зоны. Но ведь меридиан на поверхности Земли – линия воображаемая. Если идти по нему, то придется всё же воспользоваться для этого физической поверхностью, представляющую собой сплошные неровности.

Таким образом, на картах и планах измеряют не фактическое расстояние, а т.н. горизонтальное проложение, которое является проекцией линии местности на горизонтальную плоскость (рис. 2.30). При этом принято величину измеренного на карте отрезка называть расстоянием.

При измерении расстояний на топографических картах или планах используют различные виды масштабов. В § 6 были рассмотрены численный и именованный масштабы (напомним: численный масштаб 1:5000, соответствующий ему именованный масштаб – «в 1 см 50 м»). Под численным и именованным масштабами, записанными под южной рамкой карты, располагают линейный масштаб.

 

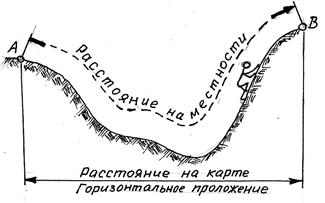
Рис. 2.30. Расстояние на местности и горизонтальное проложение.

 

Линейный масштаб (рис. 2.31) – это графическое изображение численного или именованного масштабов. Отрезок а линейного масштаба называют основанием. Первое основание делят на отрезки величиной 1 мм, что обеспечивает графическую точность отсчета до 0,1 мм.

 

 

Рис. 2.31. Линейный масштаб.

Пример 2.10. На карте масштаба 1:25000 измерено расстояние, которое получилось равным 36,7 мм.

Определить расстояние на местности.

Решение.

При использовании численного масштаба соответствующее расстояние на местности будет равно 36,7 мм х 25000 = 917500 мм = 917,5 м.

При использовании именованного масштаба (в 1 см 250 м) отрезок 36,7 мм = 3,67 см на местности будет соответствовать отрезку 3,67 см х 250 = 917,5 м.

При использовании линейного масштаба величину измеряемого отрезка необходимо взять в раствор циркуля-измерителя и перенести его на шкалу линейного масштаба. Искомый отрезок будет определён непосредственно по линейному масштабу.

 

Следует заметить, что при использовании численного и именованного масштабов получается одинаковый ответ, а при использовании линейного масштаба полученная величина может несколько отличаться от вычисленной из-за графических погрешностей, возникающих при использовании измерителя и при отсчете по шкале линейного масштаба, а также из-за возможной деформации листа топографической карты. В последнем случае применение линейного масштаба является предпочтительным, поскольку при использовании численного или именованного масштабов иногда бывает необходимо определять коэффициент деформации и вводить его значение в результат измерения. Но это при использовании карт и планов, выполненных на бумажном носителе. Электронные карты и планы таким дефектом не обладают.

Использование поперечного масштаба

Для точного графического нанесения точек на топографические план и карту, а также при построении на карте и плане точек по их координатам, используют поперечный масштаб.

 

 

Рис. 2.32. Поперечный масштаб.

 

Поперечный масштаб (рис. 2.32) представляет собой особую графическую шкалу (номограмму), основанием которой служит линейный масштаб. Линейный масштаб достраивают вертикальной шкалой с разбивкой её, например, так же, как и основания, на 10 частей по вертикальному направлению. Наклонными линиями (трансверсалями) соединяют нижние деления с верхними.

Число делений n горизонтального отрезка шкалы поперечного масштаба и число делений m вертикального отрезка может быть различным. При n = m = 10 поперечный масштаб называют нормальным или сотенным. Основание а нормального поперечного масштаба чаще всего делают равным 2 см. В соответствии с этим, цена деления меньшего отрезка основания будет равна 2 см: 10 = 0,2 см = 2 мм. При перемещении вверх (вниз) по трансверсали на один шаг соответствующий горизонтальный отрезок увеличится (уменьшится) на величину 0,2 см: 10 = 0,02 см = 0,2 мм или на величину (а: 100). Таким образом, перемещение на один шаг по трансверсали составит 1:100 основания.

 

Пример 2.11. Необходимо определить длину отрезка АВ, взятого в раствор измерителя с планов различных масштабов.

Решение.

На рис. 2.32 приведена оцифровка основания поперечного масштаба в соответствии с используемым масштабом плана и величины наименьших отрезков основания и трансверсали.

Обратите внимание на то, что отрезки АВ, 2-2, 3-3 располагаются на трансверсали между горизонтальными линиями, что даёт возможность точнее определить их длину.

Для масштаба 1:500 отрезок АВ можно представить в виде следующего набора: два полных основания (20 м), плюс восемь полных делений основания (8 м), плюс шесть с половиной делений по трансверсали (0,65 м) = 28,65 м.

Для масштаба 1:2000 АВ = 2 х 40 м + 8 х 4 м + 6,5 х 0,4 м = (80 + 32 + 2,6) = 114,6 м.

Определите значения отрезка АВ для других масштабов.

 

Пример 2.12. Отложить на поперечном масштабе отрезок L заданной длины в масштабе соответствующего плана.

Решение: приведено на рис. 2.32.

Построение отрезка 1-1 длиной 14,9 м в масштабе 1:500 (основание равно 10 м): отрезок содержит одно полное основание (10 м); остаток 14,9 – 10,0 = 4,9 м содержит четыре полных деления основания (4 м); остаток 4,9 – 4,0 = 0,9 м содержит девять делений (переходов) по трансверсали.

Построение отрезка 2-2 длиной 16,5 м в масштабе 1:1000 (основание равно 20 м): отрезок меньше основания, поэтому один его конец будет находиться на нулевой вертикальной линии; в длине отрезка содержится восемь полных делений основания (16 м); остаток 16,5 – 16,0 = 0,5 м соответствует перемещению по трансверсали вверх на два с половиной деления (в одном делении по трансверсали 0,2 м).

Аналогичным образом построены отрезки 3-3 (305,5 м в масштабе 1:5000) и 4-4 (104,4 м в масштабе 1:2000). Проверьте результаты построения и потренируйтесь в решении подобных задач.

В проекции Гаусса-Крюгера линейные измерения по карте сложностей не вызывают, тем более, что в пределах листа рабочей карты изменение масштаба длин практически не ощущается. Другое дело обстоит с часто используемой в пришельфовой зоне проекцией Меркатора. В этой проекции, например, для средних широт и экваториальной части весьма близкой к проекции Гаусса-Крюгера, простым измерением расстояния ограничиться нельзя. Взяв отрезок в раствор циркуля-измерителя, его необходимо перенести на рамку карты (примерно в том же месте) и по минутным разбивкам (меткам) по широте на рамке карты получить искомую длину.

О минутных метках будет сказано дальше, в п. 17.2.

Для измерения расстояний используют и механические приборы, которые называются курвиметрами (от латинского слова сurvus – кривой, изогнутый). Слово составное, поэтому не сам прибор кривой, это прибор, который позволяет измерять длины кривых линий на плоскости. Они, курвиметры, представляют собой устройство, измерительная часть которого снабжена колесиком, связанным со счетным барабаном. Курвиметр указывает длину пройденного пути в миллиметрах. Для определения расстояния на карте или плане необходимо учесть их масштаб. Точность измерений механическими курвиметрами порядка 0,5%.

В настоящее время на рынке геодезических приборов представлен большой выбор электронных курвиметров, которые дают возможность вводить масштаб картографического материала и определять сразу измеренное расстояние в метрах, километрах. Можно отметить такие зарекомендовавшие себя приборы, как Scale Master II, Scale Master Pro XE, PLANCOM CV-9Jr, PLANCOM CV-98USB и др. Точность измерения расстояний электронными приборами составляет 0,2% при скорости измерений до 2 м/с. Информация о результатах измерений выводится на дисплей прибора.

Впрочем, реализовать такую скорость измерений практически и невозможно.

 

17.2. Определение географических и прямоугольных координат

 

Определение географических координат.

 

И мелькают города и страны,

параллели и меридианы…

(Из геологической песни)

 

Мелькают! А разве они мелькают, если на карте изображены всего два меридиана и две параллели, которые и ограничивают этот лист: по долготе – меридианами и по широте – параллелями. Географические координаты указанных меридианов (западного и восточного) и параллелей (северной и южной) определяются по схемам разграфки карт при образовании их номенклатуры (см. § 10). Таким образом, точки или объекты местности, изображённые на листе топографической карты, имеют географические координаты в пределах разности долгот Δ λ = (λ_В – λ_З) и разности широт Δ φ = (φ_С – φ_Ю). Здесь индексы В, З, С, Ю относятся к восточной, западной, северной и южной рамкам карты.

Но в песне этой поётся о том, что «глобус крутится-вертится», а не топографическая карта. Так что на глобусе «мелькание» меридианов вполне ощущается, а вот «мелькание» параллелей весьма проблематично. Вместе с городами и странами мелькать могут только меридианы. Параллели выглядят на крутящемся глобусе (если он, конечно, не сломан и стоит с наклоном на ножке, как ему и полагается) немелькающими ниточками.

Кстати, слово меридиан происходит от латинского слова meridianus – полуденный.

Здесь следует напомнить, что на плоскости, которую представляет собой карта, географические и прямоугольные координаты, каждая из систем отдельно, однозначно определяют положение искомой точки в плане. А это означает, что между географическими (точнее – геодезическими) и прямоугольными координатами существует функциональная зависимость:

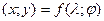. (2.19)

С такой зависимостью Вы встретитесь при изучении дисциплины «Высшая геодезия» при выполнении работы, связанной с перевычислением прямоугольных координат из зоны в зону.

Автор с Вами согласен, да и Вы тоже не будете сильно возражать, что использование в практической жизни на суше или даже на реке или озере географических координат является не совсем удобным. Пусть даже они и являются сопряженными с прямоугольными координатами, перевычисляемыми друг в друга. Прямоугольные координаты понятнее нам, потому что мы реально представляем, что такое 1,5 км или 1500 м. А вот если будет произнесено «2 градуса» или, что совсем неприятно, «6 минут 38 секунд», а последнее может восприниматься как время, а первое может восприниматься как температура, то ничего определенного сказать мало кто сможет. Да и специалист знает, что метры на Луне и метры на Земле – одно и то же, а вот в переводе на градусы, минуты и секунды положение изменяется. Не говорим же мы: «Пойдешь прямо, потом, через два квартала, примерно в 8 секундах и будет этот дом». Это вместо того, чтобы сказать – «примерно в 250 м и будет этот дом».

Для удобства в определении географических координат и повышения точности разности долгот и широт на карте разделены на минутные метки (рис. 2.33), которые, в свою очередь, точками поделены на 6 равных интервалов по десять секунд в каждом из них.

Получается как бы прямоугольная система координат с осями, являющимися рамкой карты и единицами измерения – градусами, минутами и секундами. Но, все-таки, «как бы», потому что рамка карты представляет собой в проекции трапецию, да и параллели и меридианы, в основном, линии не прямые, а сложные кривые, просто «на глаз» это не заметно. В связи с этим юго-западный, например, угол между проекцией меридина 22^о30' и проекцией параллели 54^о55' не прямой.

Определение географических координат т. А заключается в построении через неё параллели и меридиана. Полученные географические координаты этих линий и будут определять географические координаты искомой точки. Построение параллели и меридиана выполняется с помощью большой линейки с ровным краем, перекрывающей внешнюю рамку карты. Линейку необходимо установить так, чтобы её ребро проходило через т. А и через одинаковые отсчеты широты (долготы) на соответствующих минутных метках.

Вы правильно заметите, что как же можно использовать прямую линейку для построения параллели или меридиана, если эти линии являются сложными кривыми?

В пределах графической точности определения координат точек на карте кривизна линий настолько незначительна, что кривую линию параллели или меридиана с допустимой погрешностью можно считать прямой. Просто, считая их прямыми, не следует забывать, что не всё так просто.

 

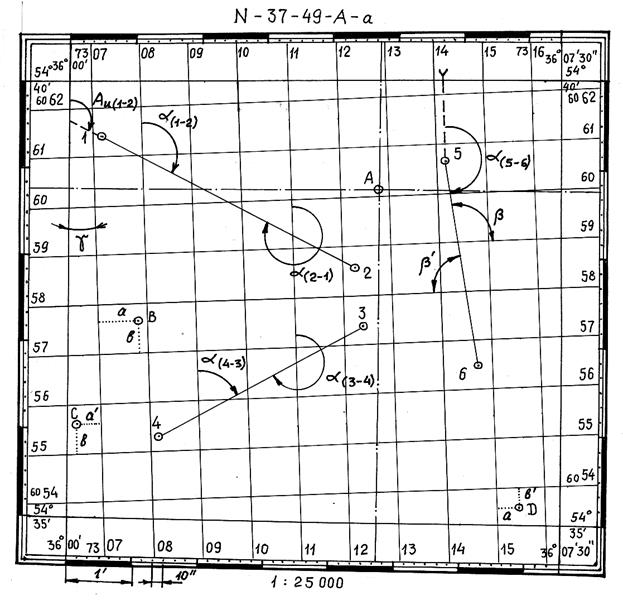
Рис. 2.33. Определение по карте географических и прямоугольных координат.

 

Для топографических карт малых и средних широт, представляющих собой практически прямоугольник (как напоминатние о предыдущем абзаце), для определения широты или долготы можно воспользоваться треугольником с прямым углом. В этом случае проектирование точки А на шкалы широт и долгот производится по перпендикуляру к рамке карты. Таким образом, долгота точки А λ_А = 36º04'44" (восточная), широта φ_А = =54º38'45" (северная).

Можно решить и обратную задачу: нанести на карту точку по её географическим координатам. Для этого с помощью большой линейки необходимо построить меридиан с долготой, равной долготе точки, и параллель с широтой, равной широте точки. На пересечении графически полученных меридиана и параллели и будет находиться искомая точка.

Определение прямоугольных координат

А вот линии километровой сетки на топографической карте «мелькают», поскольку сетка прямоугольных координат на топографической карте строится сравнительно густой в виде квадратов, одни стороны которых параллельны оси х прямоугольной системы координат и перпендикулярны оси у, а другие, наоборот, перпендикулярны оси х и параллельны оси у. В зависимости от масштаба карты подписи километровых линий производятся через определённый шаг, выраженный в километрах. Например, для карт масштабов 1:10000, 1:25000 и 1:50000 этот шаг равен 1 км, для карты масштаба 1:100000 – 2 км. Километровые линии подписывают на внешней рамке карты (рис. 2.33) двумя последними цифрами километров. Полные координаты х и у подписывают только у крайних на листе карты километровых линий.

Сокращенными координатами точки называют квадрат, в котором она находится. Обозначение квадрата складывается из значения горизонтальной и вертикальной линий километровой сетки для юго-западного его угла. Так, точка А находится в квадрате 6012, точка В – в квадрате 5707, точка С – в квадрате 5506, точка D – в квадрате 5315.

Конечно, в квадрате имеется практически бесчисленное число точек, сокращенные координаты которых будут одинаковыми. Но это очень удобно для быстрого поиска на карте заданной точки. Вы в этом сами убедитесь, когда будете работать с топографической картой.

Определение прямоугольных координат т. В сводится к измерению отрезка а по оси у и отрезка b по оси х. Величину отрезка можно определить любым из способов, рассмотренных в разделе 17.1.

В некоторых случаях точка может находиться в неполном квадрате – точки С и D. В рассматриваемом случае координата х точки С определяется так же, как и соответствующая координата т. В. Для определения координаты у _С необходимо измерить отрезок а´ и вычесть его из координаты линии 7307 км. Для точки D координата у_D определяется сложением координаты 7315 км и отрезка а, а для определения координаты х_D необходимо измерить отрезок b´ и вычесть его из координаты 6054 км.

Автор напоминает, что запись координаты у = 7315 км не означает – «семь тысяч триста и т.д.». Вспомним, что впереди координаты у приписывают номер зоны. В данном случае номер зоны – 7.

В табл. 2.6 представлен пример определения координат точек В, С и D.

Здесь также можно решить и обратную задачу: нанести точку на карту (план) по её прямоугольным координатам. Для этого необходимо определить квадрат, в котором находится данная точка, а затем, пользуясь измерителем и линейным масштабом карты, либо именованным масштабом, либо поперечным масштабом, отложить в полученном квадрате отрезки а и b. Для повышения точности построения точки сначала следует отложить по разным сторонам квадрата отрезки а (или b), а затем по полученной линии отложить отрезок b (или а).

Таблица 2.6

Пример 2.13. Определение прямоугольных координат (масштаб карты 1:25000)

Точки	Сокра-щенные коорди-наты	Величина отрезка а (а´)	Величина отрезка b (b´)	Координаты
на карте, мм	на мест-ности, м	на карте мм	на мест-ности, м	Х, км	У, км
В		32,1	802,5	26,7	667,5	6057,668	7307,803
С		19,2	480,0	24,8	620,0	6055,620	7306,520
D		17,3	432,5	15,5	387,5	6053,622	7315,433

 

Х _В = 6057 км + 0,6675 км = 6057,668 км Х _C = 6055 км + 0,6200 км = 6055,620 км

У _В = 7307 км + 0,8025 км = 7307,803 км У _C = 7307 км - 0,480 км = 7306,520 км

Х_D = 6054 км - 0,3875 км = 6053,622 км

У_D = 7315 км + 0,4325 км = 7315,433 км

 

17.3. Ориентирование линий

Измерение дирекционных углов

В § 16 дано определение дирекционного угла, как горизонтального угла, отсчитываемого по часовой стрелке от северного направления осевого меридиана до направления линии. Поскольку линии километровой сетки параллельны осевому меридиану зоны, то значение дирекционного угла в пределах зоны для одной и той же линии остается постоянным. В связи с этим и измерение дирекционного угла можно производить от вертикальной линии километровой сетки (рис. 2.33), а также пользоваться как вспомогательными и горизонтальными линиями этой сетки.

Так, дирекционный угол направления 1-2 измеряется непосредственно полукруглым (или круглым) транспортиром, а дирекционный угол направления 2-1 можно получить как сумму (α_1-2 + 180^о). Такие же измерения выполняют и для линии 3-4 (прямого и обратного направлений).

В некоторых случаях дирекционный угол может быть получен как слагаемое или разность для вспомогательных углов. Так, дирекционный угол, например, линии 5-6 (α_5-6) не может быть определен непосредственно от вертикальной линии 14 или 15 километровой сетки. В связи с этим придется выполнять дополнительные графические построения, что приведет к увеличению ошибки измерения угла. В таких случаях измеряют вспомогательный угол. Из чертежа видно, что угол β больше 90^о на угол t, а дирекционный угол α_5-6 на то же значение меньше 180^о, т.е.

α₅₆ = 180^о – (90^о – β) = 180^о – t. (2.20)

Точность измерения дирекционного угла на карте зависит от качества графических построений линии и точности транспортира. Линии следует проводить толщиной не более 0,1 мм. Геодезический транспортир (круглый или полукруглый) имеет цену деления 30΄, при этом оценка дробной части наименьшего деления производится «на глаз» до 5΄.

 

Измерение истинного азимута

Истинный азимут отсчитывается от северного направления истинного меридиана, которым являются западная или восточная рамки карты (рис. 2.33, линия 1-2).

Автор напоминает, что понятие истинный азимут относится к объединённому понятию геодезический азимут и астрономический азимут, когда пренебрегают уклонениями линий силы тяжести.

Для западной рамки карты значение измеренного истинного азимута линии 1-2 определяется в точке пересечения линии с рамкой карты. Если линия своим продолжением не пересекает западную или восточную рамки карты, то измерить её истинный азимут непосредственно не представляется возможным без дополнительных построений. В этом случае истинный азимут вычисляют по значению измеренного дирекционного угла и величине сближения меридианов γ (§ 16).

Линии километровой сетки образуют угол с западной и восточной рамкой карты. Этот угол и является углом сближения меридианов γ (на рисунке γ - восточное). Для карт центральной части зоны, величина сближения меридианов близка к нулю, в связи с чем вертикальные линии километровой сетки получаются практически параллельными западной и восточной рамкам карты.

· Склонение на 1993 г. западное 3о18΄.Среднее сближение меридианов западное 1о46΄. При прикладывании буссоли (компаса) к вертикальным линиям километровой сетки среднее отклонение магнитной стрелки западное 1о32΄. Годовое изменение магнитного склонения восточное 0о04΄. Поправка в дирекционный угол при переходе к магнитному азимуту плюс 1о32΄.

Рис. 2.34. Сетка меридианов.

 

Решение задач по ориентированию

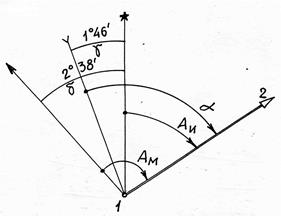
При определении ориентирующих углов на карте обычно измеряют дирекционный угол, поскольку наличие большого числа линий километровой сетки позволяет решить эту задачу сравнительно легко и точно (имеется в виду – графически точно). Истинный азимут и магнитный азимут вычисляют с учётом данных, которые приводятся в левом нижнем углу карты (рис. 2.34).

 

Пример 2.14. Ориентирование линий.

На карте измерен дирекционный угол α = 63^о35΄.

Определить истинный азимут и магнитный азимут на 2003 г.

Решение.

Истинный азимут этой линии А_И = α + γ = 63^о35΄ + (- 1^о46΄) = 61^о49΄.

Для вычисления магнитного азимута предварительно необходимо определить склонение на 2003 г.:

δ₂₀₀₃ = δ₁₉₉₃ + Δδ (2003 – 1993) = -3^о18΄ + (+0^о04΄) · 10 = -2^о38΄ (западное).

В этом случае поправка в дирекционный угол

Δα = δ₂₀₀₃ – γ = -2^о38΄-(-1^о46΄)= - 0^о52΄.

Следовательно А_М(2003) = α + Δα = 63^о35΄ - (- 0^о52΄) = 64^о27΄.

Такой же ответ получится и при вычислении магнитного азимута через истинный азимут: А_{М (2003)} = А_И – δ₂₀₀₃ = 61^о49΄ - (-2^о38΄) = 64^о27΄.

 

При использовании в решении задачи сетки меридианов взаимное расположение меридианов получается наглядным, что уменьшает вероятность ошибки в арифметических действиях.

 

17.4. Ориентирование карты на местности

Ориентирование по местным предметам

Это самый простой способ ориентирования. Наблюдатель должен находиться в опознанной точке А. На карте, располагаемой горизонтально, следует прочертить направление на видимую из точки А точку В либо отметить это направление, например, с помощью визирной линейки, а затем «на глаз» или с помощью той же визирной линейки ориентировать линию на соответствующую точку В местности. Плоскость карты при этом развернется, и карта своим ориентированным положением будет соответствовать местности.

 

 

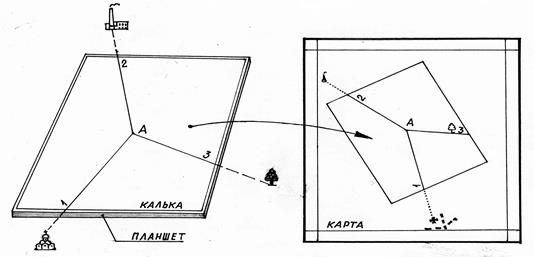
Рис. 2.35. Ориентирование по карте способом Болотова.

 

А.П.Болотов (1803-1853), генерал-майор, известный геодезист и топограф, автор книг по геодезии, работал профессором геодезии в военной академии.

 

Определение на карте точки стояния наблюдателя

Если точку А опознать затруднительно, то положение её на карте определяют с помощью прозрачной кальки, располагаемой на планшете, на которую наносят направления на опознанные на местности и карте точки (способ Болотова) – рис. 2.35. Далее кальку переносят на карту и ориентируют её таким образом, чтобы прочерченные направления прошли через соответствующие точки (объекты) местности, изображённые на карте. Место пересечения указанных направлений и определит положение т. А (наблюдателя).

 

Ориентирование карты с помощью компаса

Нулевой диаметр компаса при ориентировании прикладывают к вертикальной линии километровой сетки либо к ближней (западной или восточной) рамке карты и устанавливают стрелку компаса на север с совмещением одновременно со стрелкой его нулевого отсчета. В этом случае лист карты следует повернуть до тех пор, пока отсчёт по северному концу магнитной стрелки компаса не будет равным величине поправки в дирекционный угол, определённой по формуле (2.18). Если нулевой диаметр компаса приложить к западной или восточной рамке карты, являющимися проекциями меридианов, то учитывать необходимо только склонение магнитной стрелки, предварительно вычисленное по формуле (2.17).

 

17.5. Определение высот точек

 

Для пояснения принципа определения высот по горизонталям карт и планов воспользуемся рис. 2.25.

При определении высот точек по горизонталям необходимо учитывать следующее:

- все точки одной и той же горизонтали имеют одинаковую высоту;

- высота любой сплошной горизонтали кратна высоте сечения рельефа;

- полугоризонталь (прерывистая линия) проводится на половине высоты сечения рельефа;

- наклон местности между соседними сплошными горизонталями либо между соседними сплошной горизонталью и полугоризонталью считается однородным.

Если точка находится между горизонталями, то её высота может быть определена по формуле

Н_i = Н_Г + h_i, (2.21)

где Н_Г – высота горизонтали; h_i – превышение точки i над горизонталью.

Величину h_i определяют интерполированием заложения а по величинам отрезков m и n: h_i = Δ h (m/a) или h_i = Δ h (n/а).

В зависимости от знака превышения получают и соответствующую высоту определяемой точки.

 

Пример 2.15. Определение высот точек А, В, С, D, E, F, G (рис. 2.25).

Решение.

Точки А и В (гора). Точка А находится на горизонтали. В соответствии с указанной высотой сечения рельефа (1 м) высота соседней с вершиной горы горизонтали, кратная 1 м, составит 123 м. Следовательно, Н_А = 123 м.

Точка В «на глаз» находится посредине между горизонталями 121 и 122 м, считая их высоты вниз от горизонтали 123 м. Значит Н_В = 121,5 м.

Точка С (котловина). Здесь нам известна высота горизонтали и направление к понижению – в сторону дна котловины. Это определяется по указанию бергштрихов и дополнительно подписью горизонтали (основание подписи ориентировано в сторону понижения рельефа).

Определим высоту точки С интерполированием заложения а = n + m.

Точка С находится между горизонталями 130 и 140 м (при высоте сечения рельефа 10 м). Предположим, что а = 11,6 мм, n = 3,9 мм, m = 7,7 мм. Из пропорции найдем превышения

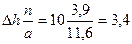м и м

точки С относительно соседних горизонталей. Высота точки С определится как Н_С = 140 – –3,4 = 130 + 6,6 = 136,6 м.

Чаще всего высоты точек по карте определяют оценкой их положения относительно горизонталей «на глаз». Это связано с тем, что ошибка построения горизонталей на карте составляет примерно 1/3 – 1/4 от высоты сечения рельефа, а ошибка оценки «на глаз» положения точки значительно меньше, порядка 1/10 от величины заложения.

Точка D (хребет). На этом фрагменте имеется подписанная высота точки местности (101,5 м). Учитывая высоту сечения рельефа (2 м), соседние с точкой 101,5 м горизонтали имеют высоты 100 и 102 м (повышение рельефа в сторону точки D). Точка D находится между горизонталью 104 м и полугоризонталью 103 м, ближе к основной горизонтали. Оценкой «на глаз» Н_D = 104 – 0,33 = 103,67 м = 103,7 м.

Точка Е (лощина). При высоте сечения рельефа 2,5 м точка Е находится между горизонталями 175 и 172,5 м, посредине между ними. Таким образом, Н_Е = 175,00 – 1,25 = =173,75 м.

Точки F и G (седловина). При высоте сечения рельефа 5 м соседняя с вершиной горы горизонталь, кратная 5 м, имеет высоту 65 м.

Переместимся в точку седловины. Первые по основанию гор горизонтали, находящиеся выше точки седловины, имеют высоту 55 м. Точка F находится «на глаз» на 1,5 м выше горизонтали 55 м, т.е. Н_F = 56,5 м. Точка G находится «на глаз» посредине между горизонталями 40 и 45 м, значит Н_G = 42,5 м.

17.6. Построение профиля

 

«И в тетради в линейку косую

Без конца я твой профиль рисую…»

(Тоже из известной песни)

 

Можно совместить эти две разные задачи – построение одного и другого профилей. Но не очень увлекаться одним из них в ущерб второму. Каждому профилю – своё время. Почти по Екклесиасту-проповеднику: есть время строить профиль, и есть время его использовать; есть время рисовать профиль, и есть время любоваться нарисованным.

Может быть то, о чём дальше будет рассказано, не очень увлекательная задача. И даже без таких сомнений. Но построение профиля – работа весьма и весьма часто выполняемая при строительстве линейных сооружений (автомобильных дорог, железных дорог, трубопроводов и т.п.), в геологии, в маркшейдерском деле и др.

Профиль – это вертикальный разрез рельефа местности по заданному направлению. Получается, как это определено для одного из значений слова профиль в «Словаре русского языка», вид сбоку.

Топографические профили местности используются для решения большого числа различных инженерных задач: при составлении предварительных проектов строительства инженерных сооружений линейного типа, при составлении геологических разрезов, при определении на местности линий видимости между выбранными точками, для составления описания рельефа по выбранному маршруту и др.

Пример построения профиля по направлению АВ показан на рис. 2.36 при высоте сечения рельефа, равной 5 м (карта масштаба 1:25000).

Далее, в качестве примера, приводится последовательность построения профиля местности.

1. Провести на карте карандашом линию АВ, направление которой определяет решение той или иной специальной задачи.

2. Оценить максимальную и минимальную высоту по линии профиля. Оценку можно выполнять с запасом на высоту сечения рельефа.

Н_max ~ 85 м; Н_min ~ 60 м.

3. Задать горизонтальный и вертикальный масштабы профиля.

Горизонтальной линией профиля является ось расстояний, вертикальной линией – ось высот. Масштабы профиля, построенного по топографической карте, по высоте и расстояниям различные. Обычно горизонтальный масштаб профиля равен масштабу топографической карты, с помощью которой он строится, а вертикальный масштаб принимают в 10 раз крупнее горизонтального. Например, масштаб карты 1:50000. Следовательно, горизонтальный масштаб профиля равен 1:50000, а вертикальный масштаб – 1:5000. В некоторых случаях, для большей наглядности, применяют более крупные масштабы высот либо укрупняют и горизонтальный масштаб. При этом для основания масштаба рекомендуется выбирать числа: 1; 2; 2,5; 5 (1:1000, 1:200, 1:50 и т.п.).

В примере горизонтальный масштаб 1:25000 (в 1 см 250 м). По правилам, которые применяются, например, в геологии, вертикальный масштаб должен быть 1:2500 (в 1 см 25 м). Но мы примем в нашем случае для наглядности вертикальный масштаб 1:500 (в 1 см 5 м).

4. Построить оси координат профиля и оцифровать их в соответствии с выбранными горизонтальным и вертикальным масштабами. При этом горизонтальный масштаб не оцифровывается, а в выбранном масштабе изображается длина всего профиля.

5. Указать высоту условного горизонта.

Условный горизонт (УГ) – это линия, абсолютная высота которой на графике профиля подбирается так, чтобы между нижней точкой профиля и линией условного горизонта оставалось место для нанесения другой информации, в отношении которой строится сам профиль.

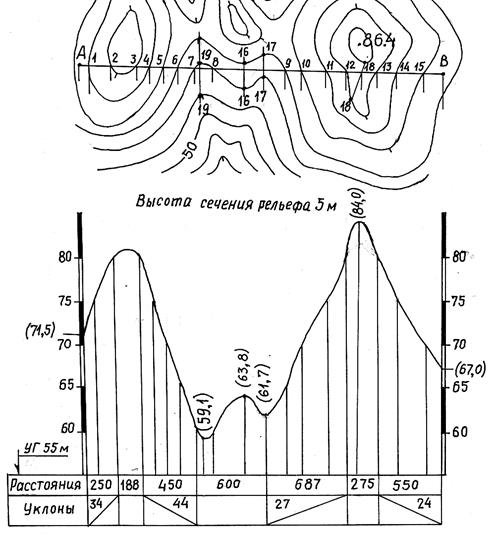
Рис. 2.36. Построение профиля местности по карте.

 

Условный горизонт УГ = 55 м.

Как Вы видите, подбор условного горизонта здесь оказался не совсем удачным. Маловато места осталось для построения какой-либо другой информации, особенно в нижней части профиля. Но это сделано только для уменьшения размера рисунка, а не как рекомендация к построению такого изображения.

6. Отложить на горизонтальной линии отрезки, соответствующие пересечениям горизонталей с линией профиля, а также точек пересечения линии профиля с объектами ситуации (дорогами, линиями связи, объектами гидрографии, границами лесов и т.п.).

7. Нанести отмеченные точки на чертеже в соответствии с их абсолютными высотами. Полученные точки соединить плавной линией.

В некоторых случаях на линии профиля можно определить высоты дополнительных точек. Если, например, точка находится между горизонталями, то ее высоту легко найти интерполированием заложения, как это пояснялось в разделе 17.5:

Н_i = Н_Г ± ( Δ h) m/а, (2.22)

где Н_Г – высота горизонтали; а – заложение; m – расстояние от горизонтали до точки линии профиля. То есть указанная задача решается аналогично определению высоты точки С (см. пример в предыдущем разделе).

При пересечении лощины (хребта) дополнительную точку определяют на линии водослива (водораздела) также методом интерполирования.

При пересечении седловины для точки седловины принимают, что она находится на половине высоты сечения рельефа от ближайшей к ней горизонтали.

Предварительно находят высоты точек А и В по правилам, приведенным выше. В примере высоты указанных точек оценим «на глаз»: Н_А = 71,5 м; Н_В = 67,0 м.

Для точки 16, находящейся на линии водораздела (на хребте), определение высоты связано с построением однородного отрезка – сечения 16-16. В этом случае превышение точки пересечения линии АВ с сечением 16-16 по отношению к горизонтали 60 определится из пропорции:

м,

где 5 м – высота сечения рельефа; 9,0 мм – заложение по сечению 16-16; 6,8 мм – расстояние по сечению 16-16 до линии АВ.

Таким образом, высота искомой точки 16 на профиле будет равна Н ₁₆ = =60,0 м + 3,8 м = 63,8 м.

Точно также можно определить указанную высоту и через другой отрезок сечения 16-16. Только в этом случае высота искомой точки 16 будет определяться через высоту горизонтали 65 м вычитанием полученной соответствующей величины 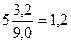м (65,0 – 1,2 = 63,8 м).

Аналогично определены высоты точек профиля по сечениям 17-17 (61,7 м), 18-18 (84,0 м) и 19-19 (59,1 м).

Если высоты точек профиля определяют дополнительно, то их значения записывают в скобках непосредственно на чертеже.

В случаях, когда высота точки не может быть определена, точки с известными высотами соединяют на профиле линией сопряжения, характеризующей форму рельефа в данном месте. Такая линия сопряжения построена между точками 2 и 3 профиля.

8. В сетке профиля выделить «на глаз» однородные склоны и вычислить для них уклоны.

Здесь следует немного остановиться, чтобы выяснить, что такое уклон?

Углом наклона ν является угол в вертикальной плоскости между плоскостью горизонта и направлением на данную точку либо направлением линии ската или заложения в выбранном месте рельефа.

Тангенс угла наклона называется уклоном i

tg ν = i. (2.23)

Величина заложения а связана с углом наклона соотношением

а= Δ h ctg ν, (2.24)

где Δ h, как Вам уже известно, – высота сечения рельефа.

В правом нижнем углу топографической карты приводят график заложений, построенный с использованием формулы (2.24) для установленной для данной карты высоты сечения рельефа. Если на карте используется два значения высоты сечения рельефа, то и график заложений на такой карте строят двойной, для соответствующих высот сечения рельефа.

Для однородной линии тангенс угла наклона равен отношению превышения h крайних точек отрезка к горизонтальному проложению d между ними, т.е

tg ν = h/d. (2.25)

В частном случае, для определения уклона местности между соседними сплошными горизонталями по заложению между ними можно записать, что

ν = arctg (Δ h / а). (2.26)

Значения уклонов задают разными способами. Простым значением тангенса угла наклона (0,0124, 0,005 и т.п.). Для сокращения записи значения уклона часто записывают его увеличенными на 1000 (0,002 → 2; 0,0236 → 23,6 и т.п.), при этом при произношении величины уклона обязательно добавляют слово «тысячных». Часто величину уклона указывают в процентах.

На профилях обычно величину уклона вычисляют до целой тысячной.

Теперь можно перейти к вычислению уклонов по линии АВ.

Для первого отрезка однородной линии профиля А-2 горизонтальное проложение равно 250 м, превышение точки 2 относительно точки А положительное (в строке «Уклоны» это отмечено соответствующим наклоном) 80,0 – 71,5 = +8,5 м. Уклон линии равен +8,5/250 = + 0,034 = 34 тысячных.

Знак «плюс» в сетке профиля не записывается, а указывается графически в виде подъема при движении от точки А к точке В.

Например, для однородного отрезка 3-7, имеющего горизонтальное проложение 450 м, превышение отрицательное, 60 – 80 = –20 м. Уклон будет равен –20/450 = – 0,0444 = – 44 тысячных.

Знак «минус» в сетке профиля не записывается, а указывается графически в виде спуска при движении от точки А к точке В.

Аналогично определены уклоны и для остальных однородных отрезков: 17-12 (27 тысячных) и 13- В (24 тысячных).

Характерными точками рельефа и ситуации на линиях профилей являются точки перегибов рельефа, линии водоразделов и водосливов (тальвеги), седловины, вершины гор (холмов), дна котловин (ям), пересечения с объектами линейного типа, гидрографией, а также и другие точки, представляющие интерес для исполнителя. Часто на разрезах (профилях) указывают границы пересечения линии АВ с площадными объектами, например, лесом, озером и т.п. Если линия профиля пересекает объект, имеющий название, например, река Токай, то и на профиле подписывают это название.

 

 

17.7. Построение линии заданного уклона

 

Как следует из формулы (2.24), увеличение угла наклона или уклона соответствует уменьшению величины заложения. И наоборот.

Значению предельного уклона i_пред соответствует и предельное значение угла наклона ν_пред, а значит и предельная величина заложения а_пред. Таким образом, при построении линии заданного уклона следует выбирать те направления на местности, по которым величина уклона не будет больше предельного либо величина заложения не будет меньше предельного его значения.

 

 

Рис. 2.37. Построение на карте линии заданного уклона.

 

Обычно решают задачу построения линии заданного предельного (возможного максимального) уклона (угла наклона).

Порядок построения линии с заданным значением предельного уклона следующий (рис. 2.37).

Предположим, что необходимо построить на карте линию АВ со значением предельного уклона i = 0,026 (ν = 1,5^о), соответствующего предельному значению заложения, показанного на рисунке. От точки А до точки 1 движение выполняется по линии АВ. Далее руч. Гремячий пересекается под прямым углом к линии водотока до точки 2. От точки 2 перемещение к точке В может осуществиться по двум вариантам (1 и 2). Здесь очевидно, что вариант 1 является оптимальным, исходя из длины общей линии АВ. Однако следует иметь в виду, что при оценке экономической целесообразности оптимальным может оказаться и второй вариант. Например, при изысканиях линейных сооружений (дорог, линий связи и т.п.) более выгодным может оказаться путь в обход лесного массива.

Возможны и другие варианты, например, вариант 3. Однако при постановке задачи проектирования кратчайшего расстояния этот вариант отпадает.

 

17.8. Построение границы водосборного бассейна и зоны затопления

Определение границы водосборного бассейна

Водосборный бассейн представляет собой ту часть земной поверхности, с которой вода, поступающая из атмосферы, стекает по склонам неровностей и собирается затем в одной точке водотока (лощины, оврага, реки и т.п.). При этом примем, что поступающая из атмосферы вода не будет поглощаться грунтом, а будет эвакуироваться по поверхности земли.

 

Рис. 2.38. Построение водосборного бассейна и зоны затопления.

 

На самом деле это не совсем так. Во-первых, часть атмосферной влаги может непосредственно перемещаться по поверхности земли к водотокам, если интенсивность поступления влаги высокая. Во-вторых, часть влаги впитывается в верхний растительный покров и эвакуируется, теперь уже медленно, по поверхности водоупорного грунта тоже в сторону водотока.

Границами водосборного бассейна являются линии водоразделов.

Для построения границы водосборного бассейна необходимо от заданной точки водотока А (рис. 2.38) подняться по линиям, перпендикулярным к горизонталям, до ближайшей водораздельной линии. Далее граница продолжается непосредственно по линиям водоразделов до их замыкания.

Используют границы водосборных бассейнов для последующего определения площади бассейна, необходимой при расчетах возможных притоков воды к отверстиям водопропускных систем под дорогами, при проектировании аэродромов и в других случаях.

Водораздельные линии строят также перпендикулярно к горизонталям по хребтам через вершины гор и точки седловин.

 

Построение зоны затопления

Указанную задачу решают при проектировании плотин либо других гидротехнических сооружений, представляющих собой препятствие для свободного тока воды.

Для построения зоны затопления исходной величиной является абсолютная высота плотины или подпорного сооружения, а также положение самой плотины 1-2 на местности. Абсолютная высота плотины задает абсолютную высоту горизонтали (рис. 2.38), которую сравнительно легко провести между горизонталями, имеющимися на карте.

Граница зоны затопления показывает на карте местность, покрывающуюся водой после строительства плотины, что необходимо для принятия соответствующих предупредительных мер. Кроме того, использование горизонталей карты и отметки водного зеркала позволяет решить задачу о ёмкости водохранилища.

 

17.9. Определение площадей на топографических картах и планах

 

Существует несколько способов определения площадей: аналитический, графический и механический.

 

Аналитический метод

Данный метод заключается в определении площади земельного участка по результатам непосредственных или косвенных измерений линий, углов. Если площади земельных участков представляют собой простые геометрические фигуры (треугольники, многоугольники и т.п.), то их площадь определяют аналитически по размерам сторон треугольников, на которые следует разбить более сложные геометрические фигуры. В этом случае, если известны, например, измерены, основания а_i и высоты h_i, то площадь S многоугольника определяется как сумма площадей нескольких треугольников (рис. 2.39 б):

. (2.27)

Если в треугольнике известны все стороны a, b и с, то для вычисления площади можно воспользоваться другой формулой

, (2.28)

где Р – полупериметр треугольника.

Если в треугольнике известны две стороны а и b и угол между ними b, то площадь находится по формуле

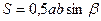. (2.29)

Площадь треугольника может быть найдена также и по известной стороне а и двум прилежащим к ней углам a и b:

. (2.30)

Если известны прямоугольные координаты вершин многоугольника (рис. 2.39 а), то значение его площади может быть получено по формуле:

(2.31)

или

. (2.32)

 

Рис. 2.39. Аналитичесий (а) и графический (б) способы определения площади многоугольника.

То есть удвоенная площадь полигона равна сумме произведений абсциссы (ординаты) каждой из точек на разность ординат последующей и предыдущей (абсцисс последующей и предыдущей) точек. Для этого следует установить направление обхода (по часовой или против часовой стрелки) и установить для каждой из точек последующую и предыдущую относительно неё точку.

В зависимости от направления обхода значение площади может получиться со знаком минус. В связи с этим значение площади всегда надо брать по абсолютной величине. Только значение площади, а не промежуточный результат.

Вычисление площади многоугольника по координатам его вершин следует выполнять для контроля по формулам (2.31) и (2.32).

 

Пример 2.16. Определение площади полигона по координатам его вершин.

Исходные данные

Точки
Х, м	2156,847	1921,315	1541,242	1756,211
Y, м	4600,212	4563,842	4781,747	4763,226

Решение.

S = 0,5 [2156,847(4563,842 – 4763,226) + 1921,315(4781,747 – 4600,212) + 1541,242 (4763,226 – 4563,842) + 1756,211(4600,212 – 4781,747)] = 0,5[2156,847 (-199,384) + +1921,315 (181,535) + 1541,242(199,384) + 1756,211(-181,535)] = 46384,816 м².

S = 0,5 [4600,212(1921,315 – 1756,211) + 4563,842(1541,242 – 2156,847) + 4781,747 (1756,211 – 1921,315) + 4763,226(2156,847 – 1541,242)] = 0,5[4600,212 (165,104) + +4563,842 (-615,605) + 4781,747(-165,104) + 4763,226(615,605)] = 46384,816 м².

Ответы совпали!

 

Графический и механический методы используются для определения площадей непосредственно на картографических изображениях.

 

Графический метод

Графический метод (рис. 2.39 б)предусматривает измерение непосредственно на плане или карте элементов сравнительно простых фигур (треугольника, прямоугольника, трапеции и др.), что позволяет затем вычислить площадь по известным формулам геометрии. Сложные фигуры разбивают обычно на треугольники, в которых измеряют основание и высоту. В некоторых случаях и площади криволинейного контура также разбивают на треугольники или другие простые фигуры.

Фигуры, на которые производят разбивку площадей объектов, должны быть по возможности крупными, мало вытянутыми, б о льшая точность будет достигаться, например, при основании треугольника, равном его высоте, опущенной на это основание.

Часто в пределах измеряемой площади имеются линии или углы, величины которых известны из результатов непосредственных измерений на местности. В этом случае необходимо разбивку привязать к этим линиям или углам, и использовать известные данные при вычислении площади.

Для повышения точности площадь фигуры следует определять не менее двух-трех раз, причем следует использовать при этом разные разбивки. Расхождение в результатах определения площади по нескольким разбивкам не должно превышать 1:50 от величины площади всего участка.

Механический метод

Механический метод определения площадей предусматривает использование палеток, ротометров, планиметров или других приборов.

Определение площадей с помощью палеток.

Принцип определения площади с помощью палетки пояснён на рис. 2.40. Палетка представляет собой прозрачную основу, на которой построена сетка квадратов с известной стороной (квадратная палетка), серия параллельных линий с известным расстоянием между ними (линейная палетка), упорядоченная группа точек с известными расстояниями между ними (точечная палетка).

При использовании квадратной палетки для данного картографического материала определяют площадь элементарной ячейки (квадрата). Например, сторона квадрата равна 2 мм, масштаб карты 1:10000. В этом случае сторона квадрата на местности будет равна 20 м, а площадь – 400 м². Палетку произвольно накладывают на фигуру и определяют число полных квадратов (N) и число всех неполных квадратов (n). Площадь определяют по формуле

S = 0,5 (2N + n) S₀. (2.33)

Рис. 2.40. Определение площади фигуры с помощью палеток:

а – квадратная палетка; б – точечная палетка; в – линейная палетка.

Пример 2.17. Определение площади с помощью квадратной палетки.

Исходные данные (рис. 2.40 а): N = 107, n = 49.

Решение.

S = 400 (107 + 49/2) = 52600 м² (при S₀ = 400 м²).

 

Похожий принцип реализуется и при использовании линейной палетки (рис. 2.40 в). В качестве единичной площади здесь выступает элементарная полоса длиной l_o, например, l_o = 1 см, при известном расстоянии а между линиями. В пределах контура фигуры измеряют длины линий посредине между нанесенными на палетку параллельными линиями, суммируют их и переводят через значение S₀ в площадь. Если крайние границы контура образуют криволинейный треугольник, как это получилось на рисунке, то величину измеренного отрезка делят пополам. То есть площадь элементарной фигуры определяется в этом случае так же, как и площадь треугольника. В примере, который приведен ниже, это учтено для соответствующих отрезков.

Пример 2.18. Определение площади с помощью линейной палетки (рис. 2.40 в).

Исходные данные (результаты измерения в пределах контура криволинейной фигуры): (9,0:2 + 17,2 + 22,4 + 24,6 + 25,0 + 25,8 + 27,0 + 27,0 + 27,2 + 29,3 + 28,0 + 28,0 + 28,5 + 25,0 + 9,4:2) мм = 344,2 мм = 34,42 см.

Площадь определяется на карте 1:5000. Расстояние между линиями палетки 2 мм. Длина единичного отрезка принята равной 1 см. Следовательно, единичная площадь S_о = 50 м · 10 м = 500 м².

Решение.

S = (500 · 34,42) = 17210 м².

 

При использовании точечной палетки (рис. 2.40 б) определяют площадь зоны влияния каждой точки, которая, вообще говоря, равна площади квадрата, как и в квадратной палетке, либо площади прямоугольника, если точки нанесены по прямоугольной сетке. В контуре подсчитывают число точек (N) и умножают его на значение элементарной площади. При этом рекомендуется не принимать во внимание точки, совпадающие с контуром измеряемой площади.

 

Пример 2.19. Определение площади с помощью точечной палетки.

Исходные данные: S_о = 200 м². N = 87 (рис. 2.40 б).

Решение.

S = 200 · 87 = 17400 м².

 

Для повышения точности площадь определяют несколько раз (5 – 6 раз) с произвольной перестановкой используемой палетки в любое положение в том числе и с поворотом относительно ее первоначального положения. За окончательное значение площади принимают среднее арифметическое из результатов измерений.

Более точным и простым в использовании является способ линейной палетки, в котором суммируются отрезки палетки, пересекающие контур.

 

Определение площадей с помощью планиметра

Планиметр был изобретен в 1850 г. русским конструктором П.А.Зарубиным (1816 - 1886). За это изобретение и последующее усовершенствование П.А.Зарубин в 1855 г. был награжден Демидовской премией (пять тысяч рублей), считавшейся самой почётной неправительственной наградой, получил золотые медали за это изобретение. Это, действительно, было замечательным изобретением, поскольку такой прибор позволяет измерять площади на картографических материалах практически любых криволинейных фигур.

Планиметр – это механический прибор, состоящий из полюсного рычага 1 с грузиком 3 (рис. 2.41). Грузик содержит в центре иглу для закрепления его в устойчивом положении на столе. На другом конце полюсного рычага имеется сферическая шарнирная головка, которая свободно вставляется в гнездо 5 обводного рычага 2. На обводном рычаге имеется обводной штырь (игла) 4 и счётный механизм 6. Счётный механизм имеет дисковую шкалу 7 счёта оборотов, счётное колесо 8, один оборот которого соответствует одному делению дисковой шкалы. Внешний ободок счётного колеса скользит по бумаге, проворачивается за счет трения и приводит в движение через червячную передачу дисковую шкалу. Со шкалой счётного колеса сопряжена шкала нониуса 9, по которой берут отсчёт дробной части наименьшего деления шкалы счётного колеса.

Полный отсчёт (рис. 2.41) содержит четыре значащих цифры: 1-я – отсчёт по шкале диска (3); 2-я – подписанное число на дисковой шкале до нулевого индекса нониуса (5); 3-я – число полных наименьших делений от ближайшей по возрастанию подписанной цифры счётного колеса до нулевого индекса нониуса (8); 4-я – ближайшее от нулевого индекса нониуса деление, совпадающее с делением шкалы счётного колеса (2). Таким образом, отсчёт равен 3582.

Последовательность измерения площади фигуры.

1. Установить планиметр на карте таким образом, чтобы при обводе фигуры угол между полюсным и обводным рычагом не был меньше 30^о и больше 150^о. При этом колесо счётного механизма обязательно должно перемещаться по поверхности бумаги. Если фигура большая, т.е. не обеспечивается поставленное выше условие, то ее следует измерять по частям. После подбора установки планиметра закрепить полюс нажатием на грузик и в дальнейшем при измерениях его не смещать.

2. Установить обводную иглу в точку фигуры, имеющей известную площадь и находящейся примерно в том же месте, что и измеряемая площадь. Такой фигурой может быть один, два или несколько квадратов километровой сетки системы прямоугольных координат карты. Если на картографическом материале отсутствуют фигуры известной площади, то можно их построить. Например, окружность известного радиуса, треугольник, квадрат и т.п. Взять начальный отсчет А_о по шкалам счётного устройства (например, А_о = 5783).

3. Аккуратно обвести фигуру с известной площадью с возвращением в начальную точку. Взять отсчет В_о (например, В_о = 5648).

4. Установить обводную иглу в точку фигуры с неизвестной площадью и взять начальный отсчет А (например, А = 4277).

5. Аккуратно обвести фигуру с неизвестной площадью с возвращением в начальную точку. Взять отсчет В (например, В = 4203).

6. Вычислить разности отсчётов

С_о = А_о – В_о и С = А – В: С_о = 5783 – 5648 = 135; С = 4277 – 4203 = 74.

7. Вычислить площадь фигуры. Предположим, что известная площадь S_о (S_о = 4 км²), тогда .

В приведенном примере: S = (4 км² · 74): 135 = 2,193 км².

Отношение

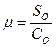(2.34)

называется ценой деления планиметра. Таким образом,

S = μС. (2.35)

Для повышения точности измерений площадь определяют несколько раз по схеме, приведенной выше. Целесообразно обвод площадей (известной и неизвестной) выполнять по часовой и против часовой стрелки, т.е. один полный прием измерения площади будет заключаться в двойном измерении. Обычно достаточно двух полных приемов. Окончательное значение площади находят как среднее арифметическое из результатов полных приемов измерений.

Если планиметр содержит два отсчётных устройства, то достаточно выполнить один полный прием, но при использовании во всех случаях двух отсчётных устройств, т.е. для каждой из точек брать по два отсчёта, например, А_о1, А_о2, В_о1, В_о2, А₁, А₂ и т.д. И, понятно, если и при использовании планиметра с двойным отсчётным усторойством выполнить измерение площади обводом по часовой и против часовой стрелке, то точность измерения будет выше.

До начала работы с планиметром необходимо выполнить его поверки в соответствии с указаниями, приводящимися в инструкции по пользованию либо в другой соответствующей литературе.

При решении различных задач требования к точности определения площадей различные. В связи с этим в каждом случае требуется выбирать и способ определения площади.

В настоящее время выпускаются планиметры различных конструкций, в том числе и электронные планиметры, выдающие результаты измерений на электронное табло. На рынке геодезических приборов представлены механические планиметры полярного типа ППМ (Россия), механические планиметры полярного типа фирмы Sokkia КР26, КР27, планиметры механические роликового типа КР46, КР92N, электронные полярного типа PLANIX 5, роликового типа PLANIX 7 и др.

Электронные планиметры имеют дисплей, а также клавиатуру для управления его работой и задания необходимых параметров, в частности, масштаба картографического материала, на котором измеряются площади фигур. Дисплей электронных планиметров имеет 8 разрядов.

Площади фигур любого контура на картографических материалах, заданных в электронном виде, измеряют по принципу планиметра. По обводе контура курсором программой обработки производится интегрирование площади по формулам (2.31) или (2.32) при использовании в расчетах большого числа вершин многоугольника, определяющих данный криволинейный контур.

 

Глава 3