Равномерным называется такое распределение случайной величины. Все значения которых лежат на некотором отрезке [а;в] и имеют постоянную плотность вероятности на этом отрезке. Таким образом, 
Так как h(b-a)=1, то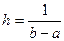 
и, следовательно
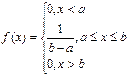
Функция распределения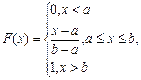 
Основные числовые характеристики:
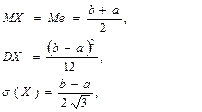
Вероятность попадания равномерно распределенной случайной величины в интервале (х1,х2), расположенной внутри отрезка [a,b]: 
.
4) Экспоненциальное распределение
Аналогом закона Пуассона для НСВ служит показательный (экспоненциальный) закон, функция плотности распределения которого имеет вид: 
, где λ>0 – постоянный параметр масштаба.
Функция распределения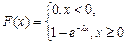 
.
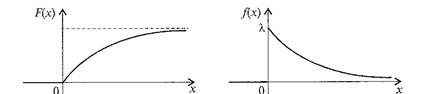
Числовые характеристики:
В теории массового обслуживания математическое ожидание экспоненциальной случайной величины – это среднее время обслуживания одной заявки.
Если Т – непрерывная случайная величина, выражающая продолжительность времени безотказной работы какого-либо элемента, а λ – интенсивность отказов (среднее число отказов в единицу времени), то продолжительность времени t безотказной работы этого элемента можно считать случайной величиной, распределенной по показательному закону с функцией распределения 
, которая определяет вероятность отказа элемента за время t.
Функция надежности определяет вероятность безотказной работы элемента за время t: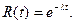 
Закон больших чисел. Центральная предельная теорема.
На практике сложно сказать какое конкретное значение примет случайная величина, однако, при воздействии большого числа различных факторов поведение большого числа случайных величин практически утрачивает случайный характер и становится закономерным.
Этот факт очень важен на практике, т.к. позволяет предвидеть результат опыта при воздействии большого числа случайных факторов.
Однако, это возможно только при выполнении некоторых условий, которые определяются законом больших чисел. К законам больших чисел относятся теоремы Чебышева.
Теорема. (Неравенство Чебышева) Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине меньше положительного числа e, не меньше чем 
.
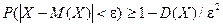
Теорема. Если Х1, Х2, …, Хn- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышаю постоянного числа С), то, как бы мало не было положительное число e, вероятность неравенства
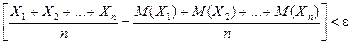
Т.е. можно записать:
Часто бывает, что случайные величины имеют одно и то же математическое ожидание. В этом случае теорема Чебышева несколько упрощается:
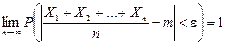
Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий.
Отклоняясь от математического ожидания как в положительную, так и в отрицательную сторону, от своего математического ожидания, в среднем арифметическом отклонения взаимно сокращаются.
Таким образом, величина среднего арифметического значений случайной величины уже теряет характер случайности.
Центральная предельная теорема Ляпунова.
Теорема. Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.
