Рассмотрим последовательность n идентичных повторных испытаний, удовлетворяющих следующим условиям:
1) Каждое испытание имеет 2 исхода, называемые успех и неуспех; это – взаимно несовместные и противоположные события;
2) Вероятность успеха – р – остается постоянной от испытания к испытанию; вероятность неуспеха – q; р+q=1;
3) Все n испытаний – независимы. Это означает, что вероятность наступления события в любом из n повторных испытаний не зависит от результатов других испытаний.
Вероятность того, что в n независимых повторных испытаниях, в каждом из которых вероятность появления события равна р, событие А наступит ровно m раз,
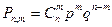
Это выражение называется формулой Бернулли.
Так как правая часть этого равенства представляет собой общий член биномиального разложения (q+p)n, то этот закон называют биномиальным.
Таким образом, биномиальным называют закон распределения ДСВ Х – числа появлений события в nнезависимых испытаниях, в каждом из которых вероятность наступления события равна р; вероятности возможных значений Х=0, 12,…,m…,n вычисляются по формуле Бернулли.
Для случайной величины Х, распределенной по биномиальному закону, имеем
МХ=np;
DX=npq;
σ(X)=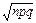 
Мода при биномиальном распределении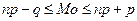 
.
Вероятность появления хотя бы одного события А при n испытаниях равна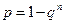 
.
Гипергеометрическое распределение.
В задачах контроля продукции часто применяется гипергеометрическое распределение, которое описывается следующей математической моделью.
Пусть во множестве из N элементов содержится k элементов с признаком В. Вероятность выбрать элемент с признаком В при одном случайном извлечении из множества равна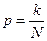 
. Пусть из множества случайным образом извлекают n элементов, одновременно или последовательно, но без возвращения. Тогда число х элементов с признаком В, содержащихся в выборке, удовлетворяет гипергеометрическому закону распределения.
Замечание. В отличии от биномиального закона, применимого в случае независимых событий, в гипергеометрическом распределении события зависимы.
Вероятность появления в выборке из n элементов ровно х элементов с признаком В вычисляется по формуле: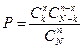 
.
Числовые характеристики:
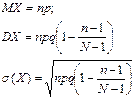
Распределение Пуассона.
Закон Пуассона называют законом редких событий, поскольку он проявляется там, где производится большое число испытаний, в каждом из которых с малой вероятностью происходит «редкое» событие. Например, число телефонных вызовов, поступивших на коммутатор за некоторый промежуток времени, число несчастных случаев, произошедших в городе за некоторый промежуток времени и т.д.
Распределение Пуассона можно описать с помощью следующей математической модели. Пусть событие А происходит многократно с течением времени, то есть имеет место поток однородных событий, который удовлетворяет следующим условиям:
1) Поток стационарен, то есть вероятность попадания k событий в промежуток времени (t; t+τ) зависит только от числа событий k и длины промежутка τ, но не зависит от начала t. Это означает, что математическое ожидание числа событий в единицу времени (плотность потока) постоянно.
2) Поток без последствия, то есть вероятность попадания k событий в промежуток времени (t; t+τ) не зависит от числа и появления событий до момента времени t, то есть имеет место взаимная независимость появления того или иного числа событий в непересекающиеся промежутки времени.
3) Поток ординарен, то есть вероятность попадания двух и более событий в промежуток времени (t; t+τ) пренебрежимо мала по сравнению с вероятностью попадания одного события в этот промежуток, то есть вероятность одновременного появления двух и более событий равна нулю.
Поток событий, удовлетворяющий условиям 1)–3) называется простейшим. Плотность простейшего потока обозначим μ.
Вероятность того, что событие А в промежутке времени τ осуществится х раз, равна
,
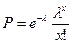где λ=μτ – среднее число событий, происходящих в промежутке времени τ.
Числовые характеристики: МХ= DX=λ, σ(X)=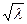 
Теорема о связи биномиального распределения с законом Пуассона.
Пусть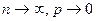 
таким образом, что произведение np остается постоянным и равным некоторому числу λ>0. Тогда вероятность того, что случайная величина, распределенная по биномиальному закону, примет значение, равное m, стремится к вероятности этого же события, вычисленной по закону Пуассона с параметром λ=np, то есть
.
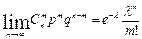Замечание. Если распределение Пуассона применяется вместо биномиального, то n должно иметь порядок не менее нескольких десятков, лучше нескольких сотен, а np<10.
