1) Для нахождения Мо НСВ необходимо проверить критическую точку функции плотности распределения (если таковая есть) на максимум и принадлежность соответствующему промежутку на котором f(x) задается. Возможно, что мода будет являться одним из концов отрезка или ее вообще не будет.
2) Медиана находится из условия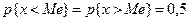 
. Решив данное уравнение, необходимо проверить принадлежность полученного решения соответствующему промежутку.
3) 
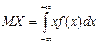. Математическое ожидание НСВ сохраняет все свойства математического ожидания ДСВ.
4) 
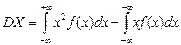. Дисперсия НСВ сохраняет все свойства дисперсии ДСВ.
5) 
6) Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени случайной величины: νk=M(Xk). Первый начальный момент – это математическое ожидание случайной величины.
При определенных допущениях относительно случайной величины по начальным моментам можно восстановить функцию распределения СВ.
7) Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины от своего математического ожидания: μk=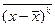 
. Дисперсия случайной величины – это второй центральный момент случайной величины.
Законы распределения НСВ.
Нормальное распределение.
Нормальное (Гауссово) распределения было открыто тремя учеными в разное время: Муавром в 1737 г. в Англии, Гауссом в 1809 г. в Германии и Лапласом в 1812 г. во Франции.
Оно возникает обычно, когда СВ Х представляет собой суму большого числа независимых СВ, каждая из которых в образовании суммы играет незначительную роль.
Нормальное распределение является предельным случаем почти всех реальных распределений вероятности. Оно широко используется в математической статистике, в частности, в моделях регрессии часто ошибка принимается распределенной по этому закону; предпосылка о нормальном распределении учитывается и в большинстве критериев статистической проверки гипотез.
Многие экономические показатели имеют близкий к нормальному закон распределения. Например, доход населения, прибыль фирм в отрасли, объем потребления и т.д. имеют близкое к нормальному распределение. Однако само нормальное распределение в экономике не используется, оно имеет чисто математический интерес.
Говорят, что СВ имеет нормальное распределение, если функция плотности вероятности имеет вид: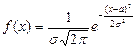 
, где МХ=а – параметр расположения, σ>0 – параметр масштаба. Чем меньше σ, тем круче график.
Функция распределения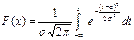 
– функция интеграла Лапласа.
График плотности вероятности нормально распределенной случайной величины называют палаткой Эйлера.
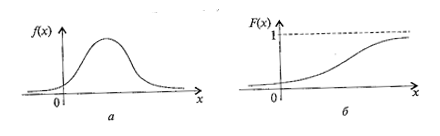
Если а = 0 и σ=1, то говорят о стандартизированном нормальном распределении с плотностью распределения 
. Эта функция четная и табулированная.
Функция распределения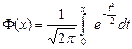 
также табулирована и обладает следующими свойствами:
1) Ф(х)=0;
2) Ф(-х)=-Ф(х);
3) Ф(-∞)=Ф(+∞)=0,5.
Для расчета вероятности попадания нормально распределенной случайной величины в промежуток от α до β используется формула: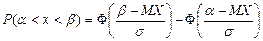 
. Эту формулу иногда называют интегральной теоремой Лапласа.
В частности, для симметричного относительно математического ожидания промежутка (МХ-Δ,МХ+Δ) можно использовать формулу 
.
С вероятностью, очень близкой к единице, все возможные значения нормально распределенной случайной величины сосредоточены на отрезке [а-3σ;а+3σ]. Это так называемое правило трех сигм: Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
Локальная теорема Муавра-Лапласа. При р≠0 и р≠1 и достаточно большом n биномиальное распределение близко к нормальному закону, причем их математические ожидания и дисперсии совпадают, т.е. имеет место равенство:
.
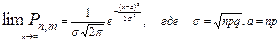Числовые характеристики. Мо=а
Ме=а
