Числовыми характеристиками дискретной случайной величины являются меры положения – характерные точки. Вокруг которых группируются значения, принимаемые случайной величиной и меры рассеивания – параметры, показывающие как группируются эти значения вокруг мер положения, каков характер этой группировки.
Основные меры положения ДСВ.
1. Мода – самое вероятное значение случайной величины (абсцисса самой высокой точки полигона вероятностей). ДСВ может не иметь моды, а может иметь несколько мод. Понятие моды работает хорошо в том случае, когда она определена однозначно.
2. Медиана ДСВ определяется так: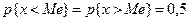 
(Me –cередина распределения вероятностей).
3. Математическое ожидание или генеральное среднее дискретной случайной величины – это средневзвешенное значение случайной величины с весами вероятностями:
МХ =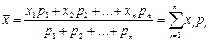 
Свойства математического ожидания:
1. Математическое ожидание постоянной равно самой этой постоянной: МС=С.
2. Константа выносится за знак математического ожидания: М(СХ)=С∙МХ.
3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий: М(Х+У)=МХ+МУ.
4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: М(Х∙У)=МХ∙МУ.
5. Для зависимых случайных величин М(Х∙У)=МХ∙МУ+kx,y, где kx,y= 
– момент корреляции случайных величин Х и У.
Меры рассеивания ДСВ.
Дисперсией ДСВ Х называется математическое ожидание квадрата отклонения этой случайной величины от ее математического ожидания: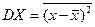 
. Дисперсия характеризует степень «сосредоточенности» или «разброс» случайной величины около ее математического ожидания.
На практике для расчета дисперсии ДСВ удобно пользоваться следующей формулой: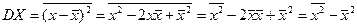 
, то есть дисперсия равна разности математического ожидания квадрата случайной величины и квадрата математического ожидания случайной величины.
При использовании дисперсии на практике возникает следующее неудобство: размерность дисперсии не совпадает с размерностью случайной величины. Поэтому используют среднее квадратическое отклонение или стандарт случайной величины: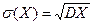 
.
Свойства дисперсии:
1. Дисперсия постоянной равна нулю: DC=0.
2. Постоянная выносится за знак дисперсии с возведением в квадрат: D(CX)=C2∙DX.
3. Дисперсия суммы независимых случайных величин равна сумме дисперсий: D(X+Y)=DX+DY.
4. Дисперсия произведения независимых случайных величин равна разности произведения математических ожиданий квадратов случайных величин и произведения квадратов математических ожиданий случайных величин:D(X∙Y)=D(X2)D(Y2)-(DX)2(DY)2.
Законы распределения ДСВ.
