Теорема Эйлера-Шаля доказывает, что любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра. В соответствии с этим легко доказывается, что при плоско-параллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нолю. Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например PV, CV.
При определении положения МЦС скорость любой точки может быть записана: VM=VCV+VMCV, где точка СV выбрана за полюс. Поскольку это МЦС и VCV=0, то скорость любой точки определяется как скорость вращении вокруг мгновенного центра скоростей.
Из рис. 1.5 видно, что мгновенный центр скоростей лежит в точке пересечения перпендикуляров, проведенных к скоростям точек, при этом всегда справедливо соотношение
Рис. 1.5
На нижеприведенных рисунках показаны примеры определения положения мгновенного центра скоростей и приведены формулы для расчета скоростей точек.
Для рисунка 1.6:
1. СV совпадает с точкой В VB=0. Шатун АВ вращается вокруг точки В
2.
3. МЦС лежит в «бесконечности»
4.
Рис. 1.6
Рис. 1.7
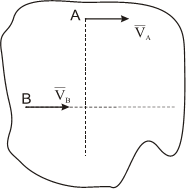
Рис. 1.8
здесь VB II VA
В этом случае МЦС находится в “бесконечности”, т.е
Рис. 1.9
Формулы справедливы при отсутствии проскальзывания в точке СV.
Рис. 1.10
РАСПРЕДЕЛЕННЫЕ СИЛЫ
В инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности по тому или иному закону. Рассмотрим некоторые простейшие примеры распределенных сил, лежащих в одной плоскости.
Плоская система распределенных сил характеризуется ее интенсивностью q, т. е. значением силы, приходящейся на единицу длины нагруженного отрезка. Измеряется интенсивность в ньютонах, деленных на метры 
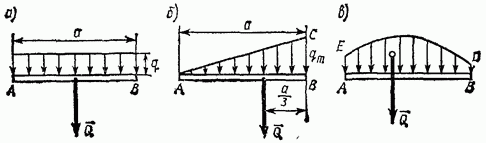
Рис. 69
1) Силы, равномерно распределенные вдоль отрезка прямой (рис. 69, а). Для такой системы сил интенсивность q имеет постоянное значение. При статических расчетах эту систему сил можно заменить равнодействующей 
По модулю,
Приложена сила Q в середине отрезка АВ.
2) Силы, распределенные вдоль отрезка прямой по линейному закону (рис. 69, б). Примером такой нагрузки могут служить силы давления воды на плотину, имеющие наибольшее значение у дна и падающие до нуля у поверхности воды. Для этих сил интенсивность q является величиной переменной, растущей от нуля до максимального значения 
Равнодействующая Q таких сил определяется аналогично равнодействующей сил тяжести, действующих на однородную треугольную пластину ABC. Так как вес однородной пластины пропорционален ее площади, то, по модулю,
Приложена сила Q на расстоянии 
от стороны ВС треугольника ABC (см. § 35, п. 2).
3) Силы, распределенные вдоль отрезка прямой по произвольному закону (рис. 69, в). Равнодействующая Q таких сил, по аналогии с силой тяжести, по модулю равна площади фигуры ABDE, измеренной в соответствующем масштабе, и проходит через центр тяжести этой площади (вопрос об определении центров тяжести площадей будет рассмотрен в § 33).
4) Силы, равномерно распределенные по дуге окружности (рис. 70). Примером таких сил могут служить силы гидростатического давления на боковые стенки цилиндрического сосуда.
Пусть радиус дуги равен 
, где 
- ось симметрии, вдоль которой направим ось 
Действующая на дугу система сходящихся сил имеет равнодействующую Q, направленную в силу симметрии вдоль оси 
при этом численно 
Рис. 70
Для определения величины Q выделим на дуге элемент, положение которого определяется углом 
а длина 
Действующая на этот элемент сила численно равна 
а проекция этой силы на ось 
будет 
Тогда
Но из рис. 70 видно, что 
Следовательно, так как 
то
где 
— длина хорды, стягивающей дугу АВ; q — интенсивность.
Рис. 71
Задача 27. На консольную балку А В, размеры которой указаны на чертеже (рис. 71), действует равномерно распределенная нагрузка интенсивностью 
Пренебрегая весом балки и считая, что силы давления на заделанный конец 
- определены по линейному закону, определить значения наибольших интенсивностей 
этих сил, если 
Решение. Заменяем распределенные силы их равнодействующими Q, R и R, где согласно формулам (35) и (36)
и составляем условия равновесия (33) для действующих на балку параллельны сил
Подставляя сюда вместо Q, R я R их значения и решая полученные уравнения, найдем окончательно
Например, при 
получим 
а при 
Задача 28. Цилиндрический баллон, высота которого равна Н, а внутренний диаметр d, наполнен газом под давлением 
Толщина цилиндрических стенок баллона а. Определить испытываемые этими стенками растягивающие напряжения в направлениях: 1) продольном и 2) поперечном (напряжение равно отношению растягивающей силы к площади поперечного сечения), считая 
малым.
Решение. 1) Рассечем цилиндр плоскостью, перпендикулярной его оси, на две части и рассмотрим равновесие одной из них (рис.
72, а). На нее в направлении оси цилиндра действуют сила давления на дно 
и распределенные по площади сечения силы (действие отброшенной половины), равнодействующую которых обозначим Q. При равновесии 
Считая приближенно площадь поперечного сечения равной 
получим для растягивающего напряжения 
значение
Рис. 72
2) Рассечем теперь цилиндрическую поверхность плоскостью, проходящей через ось цилиндра, на Две другие половины и рассмотрим равновесие одной из них, считая, что все силы приложены к ней в плоскости среднего еечени (рис. 72, 6).
На эту половину цилиндра действуют: а) равномерно распределенные по дуге полуокружности силы давления с интенсивностью 
согласно формуле (37) равнодействующая этих сил 
распределенные по сечениям цилиндра силы (действие отброшенной половины), равнодействующие которых обозначим 
причем ввиду симметрии 
Из условий равновесия 
откуда 
Так как площадь сечения, по которому распределена сила S, равна 
(площадью сечения дна цилиндра пренебрегаем), то отсюда для растягивающего напряжения 
находим
Как видим, растягивающее напряжение в поперечном направлении вдвое больше, чем в продольном.
Экзаменационный билет № 23
- Определение ускорения точки при естественном способе задания движения точки. Касательное, нормальное ускорения точки.
- Опоры и опорные реакции.
- Задача.
