Пользуясь полученными результатами, рассмотрим некоторые частные случаи движения точки.
1. Прямолинейное движение. Если траекторией точки является прямая линия, то 
. Тогда 
и все ускорение точки равно одному только касательному ускорению:
Так как в данном случае скорость изменяется только численно, то отсюда заключаем, что касательное ускорение характеризует изменение числового значения скорости.
2. Равномерное криволинейное движение. Равномерным называется такое криволинейное движение точки, в котором числовое значение скорости все время остается постоянным: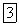 
. Тогда 
и все ускорение точки равно одному только нормальному ускорению:
Вектор ускорения а направлен при этом все время по нормали к траектории точки.
Так как в данном случае ускорение появляется только за счет изменения направления скорости, то отсюда заключаем, что нормальное ускорение характеризует изменение скорости по направлению.
Найдем закон равномерного криволинейного движения. Из формулы (17) имеем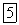 
Пусть в начальный момент времени 
точка находится от начала отсчета на расстоянии 
Тогда, беря от левой и правой частей равенства определенные интегралы в соответствующих пределах, получим
так как 
Окончательно находим закон равномерного криволинейного движения точки в виде
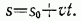
Если в равенстве (25) положить 
, то s даст путь, пройденный точкой за время t. Следовательно, при равномерном движении путь, пройденный точкой, растет пропорционально времени, а скорость точки равна отношению пути ко времени:
3. Равномерное прямолинейное движение. В этом случае 
а значит, и 
что единственным движением, в котором ускорение тонки все время равно нулю, является равномерное прямолинейное движение.
4. Равнопеременное криволинейное движение. Равнопеременным называется такое криволинейное движение точки, при котором касательное ускорение остается все время постоянным: 
Найдем закон этого движения, считая, что при 
где 
— начальная скорость точки. Согласно первой из формул 
Так как 
то, беря от обеих частей последнего равенства интегралы в соответствующих пределах, получим
Формулу (26) представим в виде
Вторично интегрируя, найдем закон равнопеременного криволинейного движения точки
При этом скорость точки определяется формулой (26).
Если при криволинейном движении точки модуль скорости возрастает, то движение называется ускоренным, а если убывает, — замедленным.
Рис. 125
Рис. 126
Так как изменение модуля скорости характеризуется касательным ускорением, то движение будет ускоренным, если величины 
имеют одинаковые знаки (угол между векторами 
острый, рис. 125, а), и замедленным, если разные (угол между 
и 
тупой, рис. 125, б).
В частности, при равнопеременном движении, если в равенстве (26) о и а, имеют одинаковые знаки, движение будет равноускоренным, а если разные знаки, — равнозамедленным.
Формулы (25) — (27) определяют также законы равномерного или равнопеременного прямолинейного движения точки, если считать 
При этом в равенствах (26) и 
где а — числовое значение ускорения данной точки [см. формулу (23)].
5. Гармонические колебания. Рассмотрим прямолинейное движение точки, при котором ее расстояние 
от начала координат О изменяется со временем по закону
где 
— постоянные величины.
Точка М (рис. 126) совершает при этом движении колебания между положениями 
Колебания, происходящие по закону (28), играют большую роль в технике. Они называются простыми гармоническими колебаниями. Величина А, равная наибольшему отклонению точки от центра колебаний О, называется амплитудой колебаний.
Легко видеть, что, начиная движение в момент 
из положения 
точка вновь придет в это положение в момент времени 
для которого 
Промежуток времени 
в течение которого точка совершает одно полное колебание, называется периодом колебаний.
Беря производные от 
по t, найдем значения скорости и ускорения точки:
Следовательно, в этом движении и скорость, и ускорение точки изменяются с течением времени по гармоническому закону. По знакам v и а легко проверить, что когда точка движется к центру колебаний, ее движение является ускоренным, а когда от центра колебаний, — замедленным.
Аналогичные колебания происходят и при законе 
только движение в этом случае начинается из центра О.
Гармонические колебания по закону 
точка может совершать, двигаясь вдоль любой кривой (см., например, в § 46 задачу 51). Все сказанное о характере движения при этом сохранится с той лишь разницей, что последняя из формул (29) будет определять касательное ускорение точки; кроме него точка будет еще иметь нормальное ускорение 
