Понятие энтропии ввёл Клаузиус, а физический смысл её выяснил Больцман. Он предположил, что энтропия связана с термодинамической вероятностью состояния системы.
Термодинамическая вероятность (статистический вес) состояния системы 
– число микросостояний (способов), которыми может быть реализовано данное макросостояние.
Пример: рассмотрим ящик, содержащий молекулы. Мысленно разделим его пополам. Если число молекул в ящике равно N =2, то возможны следующие 4 способа разместить эти две молекулы по двум одинаковым половинам ящика (рис.8.15). Таким образом, полное число способов размещения молекул N СП.=4. Термодинамическая вероятность такого состояния, когда обе молекулы соберутся в одной (например, левой) половине, равна 1: 
; это способ №1.
Число микросостояний равномерного распределения молекул равно 2: 
; это способы №3 и 4. Найдём соответствующие математические вероятности: 
и 
.
Если число молекул в ящике равно 4, то ; 
; 
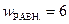и 
(рис.8.16).
Термодинамическая и математическая 
вероятности связаны между собой:
; (8.62)
здесь N СП. – число всевозможных способов распределения, и они равновероятны. Математическая вероятность всегда не больше 1, а термодинамическая не меньше 1: 
, 
.
Больцман показал, что
. (8.63)
Из формулы Больцмана (8.63) следует, что энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние.
Более вероятное состояние оказывается менее упорядоченным: для четырёх молекул ; 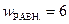. Для большого числа молекул разница окажется гораздо большей: менее упорядоченное состояние, когда молекулы распределяются равномерно, имеет существенно большую термодинамическую вероятность, чем упорядоченное состояние, когда все молекулы соберутся в одной половине ящика. Отсюда вытекает физический смысл энтропии: энтропия – мера неупорядоченности.
По второму началу термодинамики, энтропия замкнутой системы не убывает (8.43):
.
В соответствии с формулой Больцмана, это значит, что все реальные процессы идут в сторону наибольшей термодинамической вероятности; при обратимых процессах термодинамическая вероятность остаётся постоянной.
Однако при малом числе молекул (например, как в вышеприведённых примерах, две или четыре) все молекулы могут случайно в какой-то момент времени в результате теплового движения собраться в одной половине ящика. Вероятность такого события не мала: , если молекул четыре и , если две. То есть при малом числе молекул в результате флуктуаций статистический вес состояния может уменьшиться. Это происходит потому, что второе начало термодинамики неприменимо к системам с малым числом частиц.
Таким образом, второе начало термодинамики – статистический закон, выражающий закономерности большого числа частиц. В замкнутой системе, состоящей из большого числа микрочастиц, при необратимых процессах термодинамическая вероятность возрастает, при обратимых остаётся постоянной.
Если молекул в ящике много, вероятность того, что все молекулы в результате теплового движения в какой-то момент времени соберутся в одной половине, практически равна нулю: 
. Если газ первоначально находился в одной половине ящика с перегородкой, он займёт весь объём ящика, если перегородку убрать. Это необратимый процесс, так как обратный к нему процесс невозможен.
