Тепловой эффект реакции (ЛНР) не зависит от пути её протекания, а определяется только природой и физиче­ским состоянием исходных веществ и конечных продуктов

Этот закон был экспериментально установлен и имеет в настоящее время два практически важных следствия.

Согласно одному из них: Тепловой эффект реакции равен сумме теплот образова­ния продуктов реакции 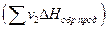за вычетом суммы теплот обра­зования исходных веществ 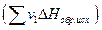с учетом числа молей (v) всех участвующих в реакции веществ:

(1.10)

В общем случае тепловой эффект 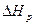реакции типа:

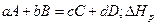
рассчитывается по уравнению

Согласно другому следствию, термохимические уравнения можно складывать, вычитать и умножать на численные множители.

В соответствии с законом сохранения энергии, система может самопроизвольно совершать "работу только за счёт собственной энергии, т.е. запас её внутренней энергии должен при этом уменьшаться или 𝛥U<0. В случае самопроизвольно протекающих химических реакций, это стремление к уменьшению запаса внутренней энергии может быть связано с выделением теплоты в виде экзотермического эффекта. Влияние этого фактора на направление самопро­извольного протекания различных процессов является одной из движущих сил химической реакции, а сам фактор называется энергетическим или энтальпийным. Но, наряду с ним, дей­ствует и другой фактор, иначе бы все химические реакции были экзотермическими. Этот фактор получил название структурного или энтропийного. Для понимания его природы не­обходимо рассмотреть ещё одну термодинамическую функцию состояния системы, полу­чившую название «энтропия».

Мерой неупорядоченности или хаотичности системы в термодинамике служит энтропия (S). Обозначим энтропию исходного со­стояния данной системы как S₁, энтропию конечного состояния как S₂, а её изменение в про­цессе как 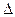S = S₂ - S_1.Поскольку из опыта следует, что S₂ > S₁, то 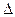S >0. Стремление же различных тер­модинамических систем к увеличению энтропии называется структурным или энтропийным фактором и его преобладающим действием объясняется самопроизвольное протекание эндо­термических процессов.

Энтропия зависит от всех видов движения частиц, составляющих систему, их количе­ства, числа степеней свободы, агрегатного состояния и возрастает с повышением температу­ры. Поэтому в процессах, вызываемых увеличением движения частиц, т.е. при нагревании, испарении, плавлении, разрыве связей между атомами и т.п., энтропия возрастает. Наоборот, упрочнение связей, охлаждение, конденсация, кристаллизация, полимеризация, т.е. процес­сы, связанные с упорядочением системы, сопровождаются уменьшением энтропии.

Энтропия пропорциональна также массе вещества. Её обычно относят к одному моль вещества и выражают в Дж/моль*К.

Энтропия является функцией состояния системы.

Энтропия, отнесенная к стандартной температуре 25°С (298К) и стандартному давле­нию (1 атм), называется стандартной (S°₂₉₈).

Одной из характерных особенностей энтропии в отличие от других термодинамиче­ских функций состояния является то, что можно определить её абсолютное значение. В тер­модинамических справочниках приводятся абсолютные значения стандартной энтропии ве­ществ при 298 К на основании которых можно рассчитать стандартные энтропии тех или иных реакций.

Изменение энтропии системы в результате протекания химической реакции (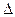 S) или энтропия реакции, как любой функции состояния системы, также не зависит от пути процес­са, а определяется лишь энтропией начального и конечного состояний:

(1.26)

При суммировании следует учитывать число молей (V) всех участвующих веществ. В общем случае изменение энтропии 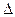S_p в результате протекания химической реак­ции типа:

рассчитывается по уравнению

(1.27)

 

ЭНЕРГИЯ ГИББСА

Для решения одной из основных задач химической термодинамики - установления принципиальной возможности самопроизвольного протекания процессов - необходимо иметь объективный количественный критерий. Выше было показано, что действующими си­лами в различных процессах (в том числе и химических) выступают две конкурирующие тенденции или два противоположных фактора:

1. Энергетический, или энтальпийный, обусловленный стремлением системы пе­рейти в состояние с наименьшей энергией, например, при р=const понизить эн­тальпию (𝛥H< 0);

2. Структурный, или энтропийный, обусловленный стремлением системы перейти в состояние с максимальной степенью разупорядоченности, т.е. повысить энтро­пию (𝛥S>0).

Если в ходе реакции степень беспорядка не изменяется (𝛥S=0), то направление процесса определяется изменением энтальпии и процесс проходит самопроизвольно в направлении уменьшения энтальпии (𝛥H< 0).

Если процесс происходит без изменения энтальпии (𝛥H=0), то фактором, определяю­щим направление реакции, является энтропия и процесс пойдет самопроизвольно в сторону её увеличения (𝛥S >0).

Если одновременно изменяются и энтальпия, и энтропия, то направление самопроиз­вольного протекания процесса определяется суммарной движущей силой реакции. Самопро­извольно реакция протекает в том направлении, в котором общая суммарная движущая сила системы будет уменьшаться.

С учетом одновременного действия этих двух противоположных факторов, такой движущей силой (функцией состояния) для реакций, протекающих при постоянной темпера­туре и давлении, является энергия Гиббса (G), называемая также изобарно-изотермическим потенциалом, или свободной энергией.

В качестве критерия для определения направления самопроизвольного протекания химических процессов (при р=const используется изменение энергии Гиббса 𝛥G или

𝛥G=G₂- G₁ (1.27)

В зависимости от знака её изменения, возможны три случая.

1. 𝛥G < 0, реакция термодинамически возможна.

При постоянной температуре и давлении химические реакции протекают самопроизвольно только в направлении уменьшения энергии Гиббса в системе (𝛥G < 0).

Это положение связано с принципом минимума энергии, лежащим в основе второго закона термодинамики, одна из формулировок которого гласит:

«Теплота не может самостоятельно переходить от менее нагретого тела к более нагретому, самопроизвольно возможен лишь обратный процесс».

2. 𝛥G > 0, реакция термодинамически невозможна;

3. 𝛥G = 0, термодинамически возможны как прямая, так и обратная реакция.

Отсутствие изменения энергии Гиббса является термодинамическим условием установления химического равновесия в реакционной системе.

Энергия Гиббса связана с энтальпией, энтропией и температурой следующим образом:

G=H-T*S

Изменение энергии Гиббcа (𝛥G) при этом записывается в виде:

𝛥G = 𝛥Н – Т𝛥S (1.28)

Из уравнения 1.28 следует, что возможность самопроизвольного протекания химических ре­акций зависит от соотношения величины 𝛥Н и Т𝛥S. При этом возможны четыре основных случая:

1. Если 𝛥Н < 0, а 𝛥S > 0, то энергия Гиббcа всегда будет величиной отрицательной (𝛥G < 0). Такие реакции термодинамически возможны при любой температуре.

2. Если 𝛥Н > 0, а 𝛥S < 0, то всегда 𝛥G > 0. Такие реакции термодинамически невозможны при любых температурах.

3. Если 𝛥Н > 0 и 𝛥S > 0, то реакция возможна только при высоких температурах, когда | 𝛥Н | < | Т𝛥S |.

4. Если 𝛥Н <0 и 𝛥S <0, то реакция возможна при низких температурах, когда | 𝛥Н | > | Т𝛥S |.

Для проведения различных термодинамических расчетов, также как и в случае других термодинамических функций, вводят специальное понятие: стандартная энергия Гиббcа об­разования вещества (𝛥G°_обр.298). Это - изменение энергии Гиббса в реакции образования од­ного моля соединения из соответствующих простых веществ, когда все участвующие веще­ства находятся в стандартном состоянии, а реакция проходит при стандартных условиях (из­меряется обычно в кДж/моль). При этом: