Гетерогенные системы содержат, по меньшей мере, две фазы.
Равновесие, которое устанавливается между фазами при физических процессах перехода веществ из одной фазы в другую, называется фазовым равновесием.
Для описания фазового равновесия систем, содержащих жидкие и газообразные фазы, например система
2Н2 (г) + О2 (г)⇄ 2Н2О (ж),
применим закон действующих масс и принцип Ле Шателье. Однако для описания системы, изменяющей свои параметры необходим количественный закон, управляющий равновесием между фазами.
К общим законам гетерогенного равновесия относится правило фаз Гиббса: число степеней свободы системы равно числу независимых компонентов минус число фаз плюс число параметров системы.
Числом независимых компонентов (К) называется число веществ в системе, достаточное для образования всех фаз данной системы. Например, в системе
CaCO3 (тв)⇄ СаО (тв) + CO2 (г)
число компонентов 3, а число независимых компонентов 2.
Число степеней свободы системы (С) – это число независимых термодинамических параметров (n) (температура, давление, электрическое поле и др.), которые можно произвольно менять в некоторых пределах без изменения числа фаз в системе.
| С = К ─ Ф + n. | (6.2.4) |
На фазовое равновесие обычно влияют температура и давление, в этом случае n = 2 и правило фаз можно записать:
| С = К ─ Ф + 2. | (6.2.5) |
Диаграммы, по которым можно определить условия устойчивости фаз и фазового равновесия, называются диаграммами состояния. Для однокомпонентных систем правило фаз имеет вид:
С = 3 ─ Ф.
Однофазная система имеет две степени свободы (С = 2) и называется бивариантной. Двухфазная система имеет одну степень свободы (С = 1) и называется моновариантной, трёхфазная система не имеет степеней свободы (С = 0) и называется инвариантной.
Примеры решения задач
Пример 1. Определить массу аммиака, объемом 1м3, который подвергнется разложению за 40 секунд, если реакция:
2NH3(г) ⇄ N2 (г) +3H2 (г)
идет со скоростью 0,02 моль/л.
Решение
Запишем математическое выражение скорости гомогенной реакции:
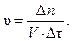
Отсюда количество молей должно быть равно:
∆ n = υ · V · ∆τ = 0,02 · 1 · 40 = 0,8 моль.
По уравнению
0,8 · 2 = 1,6 моль,
тогда масса аммиака, подвергшегося разложению:
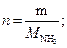
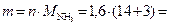27,2 г
Пример 2. Записать кинетическое уравнение и вычислить, как изменяется скорость прямой реакции, если:
а) уменьшить давление в системе в 3 раза.
б) увеличить в 3 раза концентрацию вещества А.
2А (г) + В (г) ⇄ 3С (г)
Решение
Согласно ЗДМ кинетическое уравнение прямой реакции до изменения условий запишется следующим образом:
υ пр = k [А]2 [В]
а) уменьшение давления в системе в 3 раза приведет к увеличению объема газообразной системы также в 3 раза и как следствие уменьшение концентрации также в 3 раза, тогда скорость этой реакции примет вид:
υ пр1 =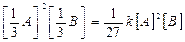 
.
Беря соотношение скоростей, определяем, что скорость реакции уменьшилась в 27 раз.
б) увеличение концентрации одного из реагентов, вызовет изменение скорости реакции и кинетическое уравнение примет вид:
υ пр1 = k ·[3A]2· [B] = 9 k ·[A]2· [B]
Беря соотношения скоростей, определяем, что скорость реакции увеличилась в 9 раз.
Пример 3
Температурный коэффициент некоторой реакции равен 3. Определить, как изменится скорость реакции при увеличении температуры с 20 °С до 60°С.
Решение. Приближенно зависимость скорость химической реакции выражается эмпирическим правилом Ван-Гоффа, математическая запись которого выглядит так:
,
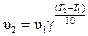В данном примере. Т 2 – Т 1= 60 °С – 20 °С = 40 °С, тогда
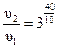= 81 раз.
Пример 4
Найдите температурный коэффициент скорости реакции разложения, если при увеличении температуры на 60.°С скорость реакции возрастает в 64 раза.
Решение. Воспользуемся эмпирическим правилом Ван-Гоффа. Температурный коэффициент можно определить:
64 =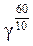 
, lg 64 = 6 · lg γ, lg γ = 
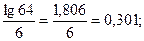γ = 2.
Пример 5. Рассчитайте энергию активации реакции, в которой при температуре 273 К константа скорости реакции равна 4,04 · 10– 5 с– 1, при увеличении температуры до 280 К константа скорости равна 7,72 ·10 – 5 с-1.
Решение. Воспользуемся уравнением Аррениуса в прологарифмированной форме.
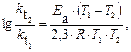
из которого энергия активации равна.
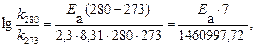
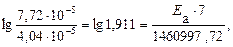
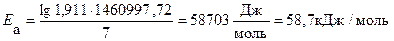
Пример 6. Как изменится равновесие реакций:
а) Н2 (г) + Br2 (г) ⇄ 2НBr (г);
б) 2H2S (г) + SO2 (г) ⇄ 3S (тв) + 2Н2О(г),
при увеличении давления?
Решение
а) из двух объемов газа образуется два объема газа. Увеличение давления не изменит равновесия.
б) из трех объемов газа исходных веществ образуется 2 объема газа продуктов реакции. Согласно принципу Ле-Шателье при увеличении давления равновесие сместится в сторону продуктов реакции.
Пример 7
Найти значение константы равновесия для реакции:
Н2 (г) + I2 (г) ⇄ 2НI (г),
если исходные концентрации Н2 и I2 равны 0,2 моль/л и 0,1 моль/л, а к моменту равновесия прореагировало 20 % иода.
Решение. Выражение константы имеет вид:
.
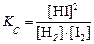К моменту равновесия прореагировало 20 % или 0,02 моль/л I2 и столько же Н2, а осталось: 0,1 – 0.02 = 0,18 моль/л Н2. Так как из 1 моля I2 и 1 моля Н2 образуется 2 моля HI, то из 0,02 моля I2 и 0,02 моля Н2 образуется 0,04 моля HI. Таким образом, равновесные концентра (моль/л):
[H2]равн= 0,18; [HI]р = 0,040.
К р = 0,042/0,18× 0,08 = 0,11.
Пример 8
Реакция протекает по уравнению
Д (г) + С (г) ⇄ 2А (г).
Определите равновесные концентрации реагирующих веществ, если исходные концентрации веществ Д и С соответственно равны 0,5 и 0,7 моль/л, а константа реакции К р = 50.
Решение
К моменту равновесия концентрации веществ Д и С понизятся. а концентрация вещества А увеличится. Так как на каждый моль веществ Д и С образуется 2 моля вещества А, то если понижение концентраций веществ Д и С обозначим через х молей, тогда увеличение концентрации вещества А будет равно 2 х молей.
Равновесные концентрации реагирующих веществ будут равны (моль/л):
[Д]р = (0,5─ х); [С]р= (0,7─ х); [А]р= 2 х.
В соответствии с этим:
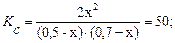
46x2 + 60x + 17,5 = 0.
Решая это уравнение, получаем: x1 = 0,86; x2 = 0,44. По условию задачи подходит значение x2. Следовательно равновесные концентрации веществ равны: (моль/л):
[Д]р = 0,5 ─ 0,44 = 0,06; [С]р= 0,7─0,44 = 0,26;
[А]р= 2 ∙ 0,44 = 0,88.
