Принцип аргумента.
В основе частотных методов лежит принцип аргумента.
Проведем анализ свойств многочлена вида:
где li - корни уравнения
На комплексной плоскости каждому корню соответствует вполне определенная точка. Геометрически каждый корень li можно изобразить в виде вектора, проведенного из начала координат в точку li: |li| - длина вектора, argli - угол между вектором и положительным направлением оси абсцисс. Отобразим D(p) в пространство Фурье, тогда 
где jw-li - элементарный вектор.
Концы элементарных векторов находятся на мнимой оси.
- модуль вектора, а аргумент (фаза) 
Направление вращения вектора против часовой стрелки принимают за ПОЛОЖИТЕЛЬНОЕ. Тогда при изменении w от 
до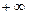 
каждый элементарный вектор (jw-li) повернется на угол +p, если li лежит в левой полуплоскости.
Пусть D(l)=0 имеет m корней в правой полуплоскости и n-m корней в левой, тогда при возрастании w до 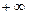изменение аргумента вектора D(jw) (угол поворота D(jw), равный сумме изменений аргументов элементарных векторов) будет 
Принцип аргумента.
    Изменение аргумента вектора D(jw) при возрастании w от до 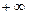равно разности (n-m) корней уравнения D(l)=0, лежащих в левой части плоскости, и числом m корней уравнения, лежащих в правой части плоскости, умноженной на p.
|
Критерий Найквиста базируется на частотных характеристиках разомкнутой цепи САУ, так как по виду частотных характеристик разомкнутой цепи можно судить об устойчивости замкнутой системы.
Критерий Найквиста нашел широкое применение в инженерной практике по следующим причинам:
1. 
Устойчивость системы в замкнутом состоянии исследуют по частотной передаточной функции ее разомкнутой цепи, а эта функция, чаще всего состоит из простых сомножителей. Коэффициентами являются реальные параметры системы, что позволяет выбирать их из условий устойчивости.
2. Для исследования устойчивости можно использовать экспериментально полученные частотные характеристики наиболее сложных элементов системы (объект регулирования, исполнительный орган), что повышает точность полученных результатов.
3. Исследовать устойчивость можно по ЛЧХ, построение которых несложно.
4. Удобно определять запасы устойчивости.
1. Система, устойчивая в разомкнутом состоянии.
Пусть 
введем вспомогательную функцию 
заменим p®jw, тогда 
Согласно принципа аргумента изменение аргумента D(jw) и Dз(jw) при 0<w<¥ равно 
Тогда 
то есть годограф W1(jw) не должен охватывать начало координат.
Для упрощения анализа и расчетов сместим начало радиуса-вектора из начала координат в точку (-1, j0), а вместо вспомогательной функции W1(jw) используем АФХ разомкнутой системы W(jw).
Формулировка критерия №1
| Если разомкнутая цепь системы устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой цепи не охватывала точку (-1, j0). |
Примеры.
Отметим, что разность числа положительных и отрицательных переходов АФХ левее точки (-1, j0) равна нулю.
Билет 24
