| Для того чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы при всех значениях w, где L(w)>0, разность числа положительных и отрицательных переходов фазовой характеристики разомкнутой системы через линии ±(2k+1)p (k=0,1,2,…) равнялась m/2, где m - число полюсов с положительной вещественной частью в передаточной функции разомкнутой цепи системы. |
Примечание: фазовая характеристика ЛЧХ астатических систем дополняется монотонным участком +np/2 при w®0.
Пример 1.
 Здесь m=0 Þ система устойчива, но при уменьшении k система может быть неустойчива, поэтому такие системы называются условно-устойчивыми.
Здесь m=0 Þ система устойчива, но при уменьшении k система может быть неустойчива, поэтому такие системы называются условно-устойчивыми.
| Пример 2.
20lgk
1/T0
Здесь  При любых k система неустойчива. Такие системы называются структурно-неустойчивыми.
При любых k система неустойчива. Такие системы называются структурно-неустойчивыми.
|
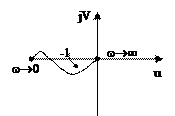 Пример 3. Пример 3.
 АФХ охватывает точку с координатами (-1, j0) 1/2 раза, следовательно замкнутая система устойчива.
АФХ охватывает точку с координатами (-1, j0) 1/2 раза, следовательно замкнутая система устойчива.
| Пример 4.
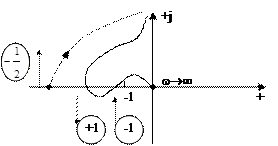
 при w®0 АФХ имеет разрыв, и поэтому ее нужно дополнить дугой бесконечно большого радиуса от отрицательной вещественной полуоси.
На участке от -1 до -¥ имеется один положительный переход и полтора отрицательных. Разность между положительными и отрицательными переходами равна -1/2, а для устойчивости замкнутой системы требуется +1/2, так как характеристический полином разомкнутой системы имеет один положительный корень - система неустойчива.
при w®0 АФХ имеет разрыв, и поэтому ее нужно дополнить дугой бесконечно большого радиуса от отрицательной вещественной полуоси.
На участке от -1 до -¥ имеется один положительный переход и полтора отрицательных. Разность между положительными и отрицательными переходами равна -1/2, а для устойчивости замкнутой системы требуется +1/2, так как характеристический полином разомкнутой системы имеет один положительный корень - система неустойчива.
|
Абсолютно-устойчивой называют систему, которая сохраняет устойчивость при любом уменьшении коэффициента усиления разомкнутой цепи, иначе система условно- устойчивая.
Системы, которые можно сделать устойчивыми путём изменения их параметров, называются структурно-устойчивыми, иначе – структурно-неустойчивыми.
Билет 22
Вопрос 1. Уравнение Статики САУ
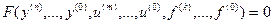 - (нелинейность несущественная) аналитическая нелинейная функция в области малых приращений.
- (нелинейность несущественная) аналитическая нелинейная функция в области малых приращений.
Если нелинейная функция F и все её производные однозначны и непрерывны, то при малых отклонениях координат она может быть разложена в ряд Тейлора в окрестности произвольно выбранной базовой точки (n+m+k+3)-мерного пространства (для САР эта точка соответствует установившемуся режиму):
 где (1)
где (1)
 так как выбранная точка (y0, u0, ¦0) – установившийся режим работы, где производные координат равны нулю, для приращений начальные условия будут нулевыми.
так как выбранная точка (y0, u0, ¦0) – установившийся режим работы, где производные координат равны нулю, для приращений начальные условия будут нулевыми.
Ф – сумма членов ряда Тейлора высшего порядка малости и ими можно пренебречь (для устойчивых САУ отклонения переменных малы, ибо этого требует сама идея работы замкнутой автоматической системы).
Уравнение установившегося режима
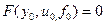 (2)
(2)






