Билет 21
Вопрос 1. Принцип обратной связи (принцип управления по отклонению контролируемой функции от входного воздействия, принцип Ползунова-Уатта)
Сущность принципа обратной связи заключается в том, что регулятор вступает в работу только тогда, когда между текущим и заданным значениями регулируемой функции появляется рассогласование, и регулятор воздействует на объект таким образом, чтобы свести это рассогласование к нулю или к малой величине.
Принцип внутренне противоречив, ибо прежде чем ликвидировать ошибку необходимо допустить ее возникновение.
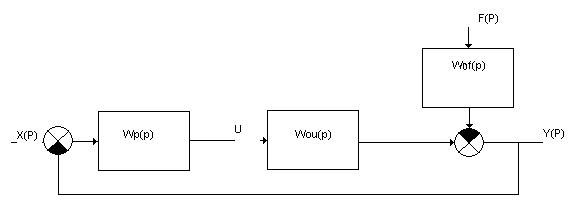
В рассматриваемом случае уравнение системы регулирования будет иметь
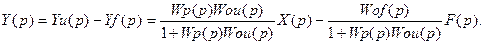
Если Wp(p) по модулю во всех режимах работы системы сделать достаточно большим [в идеале Wp(jω)®¥], то у®u, так как при этом условии Wзf(p) будет стремиться к нулю, а Wзx(p) - к единице. Следовательно, регулирование по отклонению позволяет одновременно уменьшить влияние на систему возмущающих воздействий f и увеличить точность воспроизведения заданного входного воздействия x.
| Регулятор вырабатывает в системе изменение y(t), направленное навстречу начальному отклонению, вызвавшему работу регулятора, то есть стремится компенсировать возникшее отклонение. |
Обратные связи в регуляторе или объекте называются местными обратными связями.
Если система линейная и звенья статические, то в установившемся режиме 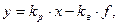
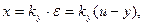 тогда
тогда 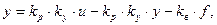 где обозначим k=kpky – общий передаточный коэффициент разомкнутой цепи регулирования.
где обозначим k=kpky – общий передаточный коэффициент разомкнутой цепи регулирования.
Уравнение статического равновесия имеет вид 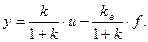
При увеличении k влияние ¦ уменьшается, поэтому достоинством этого принципа регулирования является его универсальность по отношению к возмущениям, а недостатком – склонность системы к неустойчивому режиму работы.
Установившаяся ошибка регулирования в статической системе с единичной отрицательной обратной связью (статическая ошибка)  если k>>1, то
если k>>1, то 
Достоинства:
1. Регулирование по отклонению позволяет уменьшить влияние на систему всех возмущающих воздействий;
2. Увеличивается точность воспроизведения заданного входного воздействия;
3. На динамические свойства объекта никаких ограничений не накладывается. Следовательно, регулирование по отклонению применимо к любым объектам, в том числе и к неустойчивым;
4. Отсутствие необходимости замера возмущений, что очень важно с практической точки зрения;
5. Отсутствие жёстких требований к стабильности характеристик элементов регулятора и объекта.
Недостатки:
1. Принципиально нельзя получить регулирование без ошибки, так как ошибка
регулирования является сигналом, который управляет регулирующим органом;
2. Склонность системы к неустойчивому режиму работы.
Управление – фундаментальная философская категория, решающая задачу формирования управляющих воздействий.
Регулирование – производная философская категория, решающая задачу отработки заданных воздействий.
Системы автоматического регулирования (САР) отличаются от систем автоматического управления (САУ) тем, что в последних происходит как формирование (выработка) желаемого поведения объекта на основании цели управления в виде задающих (управляющих) воздействий, так и их отработка; в САР происходит лишь их отработка, а сами управляющие воздействия, поступающие на элемент сравнения, считаются заданными.
Теория автоматического регулирования является основой построения первого уровня, а теория автоматического управления – основой всей иерархической структуры информационных процессов управления, необходимых для комплексной автоматизации сложных объектов.
Принцип действия любой САР состоит в том, чтобы обнаружить отклонения регулируемых величин, характеризующих работу машины, или протекание процесса от требуемого режима, и при этом воздействовать на машину или процесс так, чтобы устранить возникшие отклонения.
В теории автоматического регулирования основными являются проблемы: устойчивости, управляемости, наблюдаемости, качества переходных процессов, динамической точности, автоколебаний, оптимизации, синтеза и идентификации.
Пример 3. Определить уравнение статики системы регулирования напряжения генератора постоянного тока.

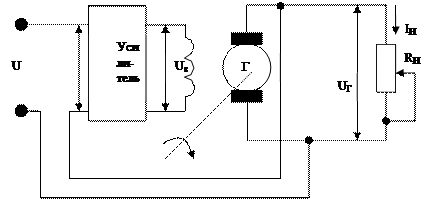
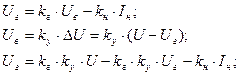

где k=kг×kу, kг=F(Uг) определяется при Iн=0.
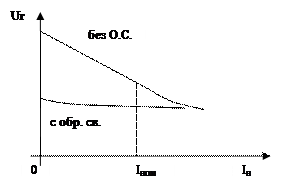
Выходная статическая характеристика САР.
Вопрос 2. Критерий Найквиста для систем, разомкнутые цепи которых кроме полюсов с отрицательными вещественными частями имеют полюса на мнимой оси.
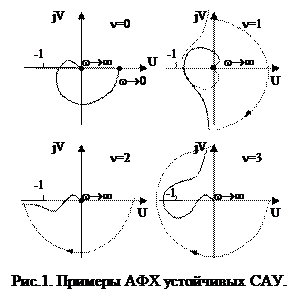
 | |||||
 | |||||
 |
Для анализа устойчивости системы АФХ дополняют окружностью бесконечно большого радиуса при w®0 против часовой стрелки до положительной вещественной полуоси при нулевых полюсах, а в случае чисто мнимых корней - полуокружностью по часовой стрелке в точке разрыва непрерывности АФХ
Формулировка критерия №2
| Если передаточная функция разомкнутой цепи системы имеет нулевые или чисто мнимые полюсы, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы с ее дополнением в бесконечности не охватывала точку (-1, j0). |
3. Система с неустойчивой разомкнутой цепью.
Более общий случай - знаменатель передаточной функции разомкнутой системы содержит корни, лежащие в правой полуплоскости. Появление неустойчивости разомкнутой системы вызывается двумя причинами:
1. Следствием наличия неустойчивых звеньев;
2. Следствием потери устойчивости звеньев, охваченных положительной или отрицательной обратными связями.
Xотя теоретически вся система в замкнутом состоянии может быть устойчивой при наличии неустойчивости по цепи местной обратной связи, практически такой случай является нежелательным и его надо избегать, стремясь использовать только устойчивые местные обратные связи. Это объясняется наличием нежелательных свойств, в частности появлением условной устойчивости, которая при имеющихся обычно в системе нелинейностях может в некоторых режимах привести к потере устойчивости и появлению автоколебаний. Поэтому, как правило, при расчете системы выбирают такие местные обратные связи, которые были бы устойчивыми при разомкнутой главной обратной связи.
Пусть характеристический многочлен D(p) разомкнутой системы имеет m корней с положительной вещественной частью.
Тогда 
Вспомогательная функция 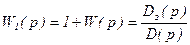 при замене p®jw согласно принципа аргумента для устойчивых замкнутых систем должна иметь следующее изменение аргумента при
при замене p®jw согласно принципа аргумента для устойчивых замкнутых систем должна иметь следующее изменение аргумента при 

Формулировка критерия №3
| Для устойчивости замкнутой системы, разомкнутая цепь которой неустойчива, требуется, чтобы амплитудно-фазовая характеристика разомкнутой цепи (с дополнением в бесконечности для систем с нулевыми и чисто мнимыми полюсами передаточной функции разомкнутой системы) охватывала точку (-1, j0) против часовой стрелки на угол mp, где m - число полюсов с положительной вещественной частью в передаточной функции неустойчивой разомкнутой цепи системы. |
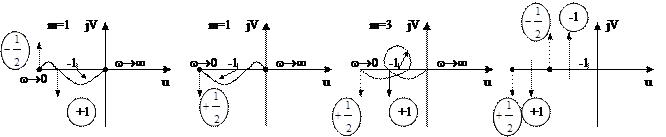
Формулировка Я.З. Цыпкина.
| Замкнутая система устойчива, если при изменении w от нуля в сторону положительных значений до ¥ разность числа положительных и отрицательных переходов АФХ разомкнутой системы через полупрямую (-¥, -1) равна m/2. |






