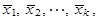
|
lze k výpočtu aritmetického průměru rovněž použít vztah (1.21). Jestliže aritmetické průměry v jednotlivých intervalech neznáme, což je v praxi častější případ, nemůžeme celkový aritmetický průměr spočítat přesně a musíme jej proto pouze odhadnout. Jsou-li všechny intervaly ohraničeny, budeme předpokládat, že aritmetický průměr v každém intervalu odpovídá středu tohoto intervalu a jednotlivé intervaly nehradíme jejich středy. Výpočet aritmetického průměru za všechny intervaly dohromady pak provedeme stejným způsobem jako výpočet váženého aritmetického průměru v prostém rozdělené četností, přičemž středy jednotlivých intervalů dosazujeme do vzorce (1.13) za obměny proměnné. V případě, že jsou krajní intervaly neuzavřené, potom se buď neuzavřený krajní interval považuje za stejně široký, jako je interval bezprostředně sousedící, a takto pomyslně vytvořené krajní intervaly se nahradí svými středy, nebo se určí minimální, resp. maximální, hodnota proměnné ve statistickém souboru a tato hodnota slouží jako odhad hranice intervalu, který potom stejným způsobem nahradíme jeho středem. Výpočet potom provedeme opět pomocí vztahu (1.13), kde za obměny proměnné opět dosazujeme středy jednotlivých intervalů, v případě krajních neuzavřených intervalů dosadíme odhadnuté středy intervalů.
Geometrický průměr
Prostý geometrický průměr n kladných hodnot x 1, x 2,..., xn, které opět nemusí být uspořádány, vypočteme jako
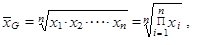
| (1.22) |
kde řecké písmeno P představuje symbol používaný pro součin hodnot. Jsou-li hodnoty proměnné již setříděny do tabulky rozdělení četností, použijeme raději vážený geometrický průměr
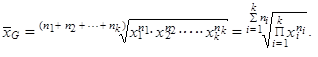
| (1.23) |
Geometrický průměr má smysl tehdy, má-li nějaký informační smysl součin hodnot proměnné.
Harmonický průměr
Prostý harmonický průměr n kladných hodnot x 1, x 2,..., xn, které nemusí být uspořádány, lze vypočítat jako
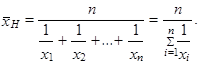
| (1.24) |
Máme-li hodnoty proměnné uspořádány do tabulky rozdělení četností, je lepší použít vážený harmonický průměr
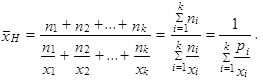
| (1.25) |
Harmonický průměr má smysl tehdy, má-li nějaký informační smysl součet převrácených hodnot proměnné. Jak plyne ze vzorce (1.24), je převrácená hodnota harmonického průměru
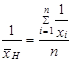
| (1.26) |
aritmetickým průměrem převrácených hodnot proměnné.
Kvadratický průměr
Prostý kvadratický průměr n hodnot x 1, x 2,..., xn, které opět nemusí být uspořádány, vypočteme jako
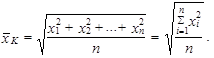
| (1.27) |
Jsou-li hodnoty proměnné již setříděny do tabulky rozdělení četností, použijeme raději vážený kvadratický průměr
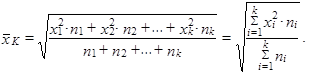
| (1.28) |
Kvadratický průměr má smysl tehdy, má-li nějaký informační smysl součet čtverců hodnot proměnné. Ze vzorce (1.27) plyne, že čtverec kvadratického průměru
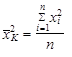
| (1.29) |
je aritmetickým průměrem čtverců hodnot proměnné.
Pro kladné hodnoty x 1, x 2,..., xn platí mezi uvedenými čtyřmi typy průměrů těchto hodnot relace nerovnosti
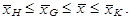
| (1.30) |
Znaménko rovnosti ve vztahu (1.30) platí pouze v případě, jestliže jsou všechny hodnoty číselné proměnné ve statistickém souboru stejné.
Příklad 1.9
U sedmi skupin studentů bydlících na koleji byla zjišťována výše měsíčního kapesného od rodičů. Průměrné měsíční kapesné od rodičů v i -té skupině budeme značit
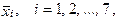
viz tabulka 1.26.
| Tabulka 1.26 | ||||
| 
| 
| ||
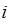
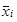
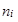
| 1 600 − 3 000 1 160 2 440 2 000 1 400 | − |
Určete chybějící údaje v tabulce, víte-li, že bylo provedeno šetření u 200 studentů a že průměrná výše měsíčního kapesného od rodičů je 1 747 Kč.
Řešení:
Průměrné měsíční kapesné od rodičů za všech k = 7 skupin studentů dohromady je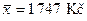 
a celkový počet studentů, u kterých bylo provedeno šetření, za všech k = 7 skupin dohromady n = 200. Vypočteme
|
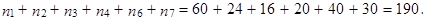
Protože
|
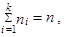
vypočteme chybějící hodnotu n 5 jako
|
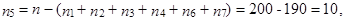
tj. získáváme
|
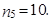
K výpočtu hodnoty
|
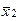
použijeme vztah (1.21), který lze napsat jako
|
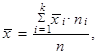
takže
|
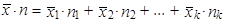
a protože k = 7
|
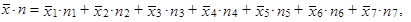
získáváme
|
|
|
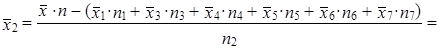
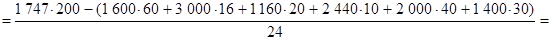
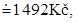
takže další chybějící údaj v tabulce je
|
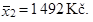
Příklad 1.10
V akciové společnosti je průměrný plat 34 000 Kč, přičemž 60 % pracovníků s nejnižším platem má průměrně 20 000 Kč. Na začátku roku došlo ke zvýšení platů pracovníků této skupiny jednotně o 2 000 Kč. O kolik procent vzrostl průměrný plat v celé společnosti následkem tohoto zvýšení nejnižších platů?
Řešení:
Celkový aritmetický průměr platu v celé akciové společnosti je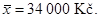 
Relativní četnost pracovníků s nejnižším platem pN = 0,6 a aritmetický průměr platu pracovníků s nejnižším platem
|
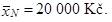
Relativní četnost ostatních pracovníků je potom pO = 1 − pN = 1 − 0,6 = 0,4 (tedy 40 %). Nejprve vypočteme aritmetický průměr platu ostatních pracovníků. Opět využijeme vztah (1.21), přičemž máme zde k = 2 skupiny, tj. pracovníky s nejnižším platem (značíme N) a ostatní pracovníky (značíme O). Tentokrát využijeme vztahu (1.21) vyjádřeného pomocí relativních četností, neboť neznáme absolutní četnosti pracovníků v jednotlivých skupinách, nýbrž pouze relativní četnosti. Ze vztahu (1.21) získáváme
 
|
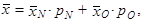
odtud
|
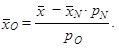
Po dosazení bude aritmetický průměr platu ostatních pracovníků
|
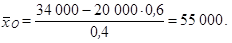
Z vlastnosti aritmetického průměru číslo pět plyne, že jestliže všem zaměstnancům akciové společnosti s nejnižším platem jednotně přidáme 2 000 Kč, aritmetický průměr platu zaměstnanců této skupiny vzroste o 2000 Kč, neboli po zvýšení platů bude aritmetický průměr platu pracovníků s nejnižším platem
|
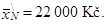
Jestliže přidáme na platu pracovníkům s nejnižším platem jednotně 2 000 Kč, vzroste tím rovněž aritmetický průměr platu pracovníků celé akciové společnosti. Opět využijeme vztah (1.21) a vypočteme nový průměrný plat za celou akciovou společnost dohromady.
|
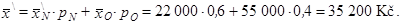
Nyní vypočteme, o kolik procent vzrostl průměrný plat v celé společnosti následkem zvýšení nejnižších platů
|
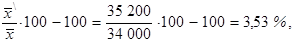
tj. průměrný plat v celé společnosti vzrostl o 3,53 %.
Příklad 1.11
Je dáno intervalové rozdělení četností, viz tabulka 1.27.
| Tabulka 1.27 | |||
| Interval | Relativní četnost | ||
| 121 − 125 126 − 130 131 − 135 136 − 140 141 − 145 146 − 150 151 − 155 156 − 160 161 − 165 166 − 170 | 0,03 0,05 0,08 0,19 0,17 0,27 0,13 0,04 0,03 0,01 |
Vypočítejte aritmetický průměr.
Řešení:
Všechny intervaly jsou ohraničeny, jednotlivé intervaly nahradíme jejich středy. Výpočty shrneme do tabulky 1.28. K výpočtu použijeme vztah (1.13). Protože známe pouze relativní četnosti v jednotlivých intervalech a nikoliv četnosti absolutní, použijeme vztah (1.13) vyjádřený pomocí relativních četností. Proto si v tabulce 1.28 ještě připravíme sloupeček xi ∙ pi.
| Tabulka 1.28 | ||||
| Střed intervalu | Relativní četnost | |||
| xi | pi | xi ∙ pi | ||
| 0,03 0,05 0,08 0,19 0,17 0,27 0,13 0,04 0,03 0,01 | 3,69 6,40 10,64 26,22 24,31 39,96 19,89 6,32 4,89 1,68 | |||
| Celkem | 1,00 |
Aritmetický průměr vypočteme následovně
|
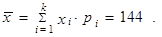
Příklad 1.12
V tabulce 1.29 jsou uvedeny koeficienty růstu prodeje automobilů značky Škoda a značek dovezených zahraničních automobilů v jednom autosalonu v letech 2001 až 2006. Koeficienty růstu jsou indexy, kde v čitateli je hodnota z období t a ve jmenovateli je hodnota z období t − 1.
| Tabulka 1.27 | ||||||||
| Rok | ||||||||
| Automobily | ||||||||
| Škoda | − | 1,136 | 1,217 | 1,154 | 0,819 | 0,934 | ||
| Zahraniční automobily | − | 1,421 | 1,568 | 1,047 | 0,825 | 1,146 | ||
Určete, zda byl v uvedeném období vyšší průměr z těchto koeficientů u značky Škoda nebo u značek zahraničních automobilů.
Řešení:
Koeficienty růstu představují relativní změny prodeje automobilů v období t oproti období t − 1. Tyto hodnoty nelze proto sčítat, smysl má však shrnutí součinem, jinými slovy průměrný koeficient růstu (průměr z koeficientů růstu) je vždy geometrický průměr. Protože je zde každý koeficient růstu obsažen pouze jednou, použijeme prostý geometrický průměr (1.22). Vždy se jedná o geometrický průměr z pěti hodnot, tudíž n = 5. Výpočet provedeme následovně
|
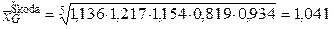
a
|
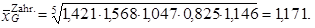
Získáváme
|
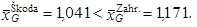
Příklad 1.13
Cena jedné akcie banky na burzovním trhu vzrostla od úterý 16. května 2006 do čtvrtka 18. května 2006 z 1 552 Kč na 1 612 Kč. Jaký byl průměrný relativní denní přírůstek ceny této akcie?
Řešení:
Relativní denní přírůstky ceny této akcie udávají koeficienty růstu. Označme:
x 16…cena akcie v úterý 16. května 2006, x 16 = 1 552 Kč,
x 17…cena akcie ve středu 17. května 2006,
x 18…cena akcie ve čtvrtek 18. května 2006, x 18 = 1 612 Kč.
Koeficient růstu kt je index
|
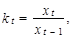
kde xt je hodnota v období t a xt − 1 je hodnota v období t − 1. Koeficient růstu z úterý 16. května 2006 na středu 17. května 2006 je
|
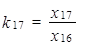
a koeficient růstu ze středy 17. května 2006 na čtvrtek 18. května 2006 je
|
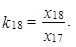
Průměrný relativní denní přírůstek ceny této akcie vypočteme opět jako geometrický průměr. Jedná se opět o prostý geometrický průměr, neboť každý z uvedených dvou koeficientů růstu je zde pouze jednou, n = 2
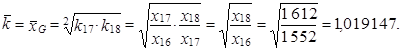(Poznámka: Výraz  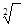je zde použit pro zdůraznění, že se jedná o druhou odmocninu)
|
Chceme-li vědět o kolik procent
|
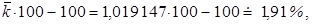
tj. denní přírůstek v průměru o 1,91 %.
Příklad 1.14
Řidič zkušebního automobilu jel do cílového místa průměrnou rychlostí 60 km/h a zpět průměrnou rychlostí 80 km/h. Předpokládáme, že trasa tam i zpět je totožná. Jakou průměrnou rychlost dosáhl řidič na celé trase?
Řešení:
Označíme x 1 = 60 km/h a x 2 = 80 km/h. Podíl
|
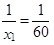
představuje, „kolik hodin (jako desetinné číslo) jel řidič v průměru jeden kilometr při cestě tam“, obdobně podíl
|
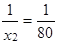
představuje, „kolik hodin jel řidič v průměru jeden kilometr při cestě zpět“. Protože obě trasy jsou stejně dlouhé a obě jel řidič pouze jednou, použijeme při výpočtu prostý vzorec. Trasy jsou dvě, tedy n = 2. Protože má smysl součet převrácených hodnot
|
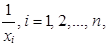
použijeme při výpočtu vzorec prostého harmonického průměru (1.24)
|
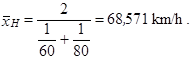
Na celé trase řidič dosáhl rychlosti v průměru 68,571 km/h.
Příklad 1.15
Automobil jel z města A do města B průměrnou rychlostí 60 km/h, z města B do města C průměrnou rychlostí 70 km/h a z města C do města D průměrnou rychlostí 80 km/h. Vypočítejte, jakou průměrnou rychlost dosáhl automobil na celé trase, jestliže:
a) vzdálenost města A a města B je 5 km, vzdálenost města B a města C je 8 km a vzdálenost města C a města D je 10 km,
b) vzdálenost města A a města B představuje 10 % celkové trasy, vzdálenost města B a města C představuje 40 % celkové trasy a vzdálenost města C a města D představuje 50 % celkové trasy.
Řešení:
a) Označme x 1 = 60 km/h, x 2 = 70 km/h a x 3 = 80 km/h, přičemž x 1 = 60 je zde n 1 = 5-krát (touto rychlostí jel automobil 5 km), x 2 = 70 je zde n 2 = 8-krát (touto rychlostí jel automobil 8 km) a x 3 = 80 je zde n 3 = 10-krát (touto rychlostí jel automobil 10 km). Tedy k = 3.Podíl
|
|
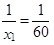
představuje „kolik hodin (jako desetinné číslo) jel automobil v průměru jeden kilometr z města A do města B “. Protože z města A do města B je n 1 = 5 km, získáváme podíl
|
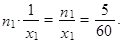
Analogickou úvahou získáváme podíly
|
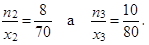
Pro výpočet použijeme vzorec váženého harmonického průměru (váženého proto, že x 1 = 60 je zde n 1 = 5-krát, x 2 = 70 je zde n 2 = 8-krát a x 3 = 80 je zde n 3 = 10-krát), protože má smysl součet podílů
|
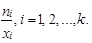
Dosadíme do vzorce (1.25)
|
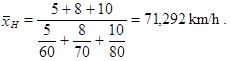
