Statistický znak je odraz určité vlastnosti každé statistické jednotky uvažovaného statistického souboru. Počet hodnot (které mohou být slovní i číselné) daného statistického znaku je roven rozsahu statistického souboru. Např. v 60 domácnostech určité obce můžeme sledovat následující statistické znaky: počet osob v domácnosti, počet dětí domácnosti, čistý měsíční příjem domácnosti, měsíční výdaje domácnosti apod.
Hodnota statistického znaku, která se často nazývá rovněž pozorování, je označení stupně uvažované vlastnosti, která je vyjádřená určitým statistickým znakem, pozorovaného u každé jednotlivé statistické jednotky statistického souboru
Statistický znak může v určitém statistickém souboru nabývat buď pouze jedné obměny, někdy říkáme varianty, nebo dvou obměn, neboli variant, nebo více obměn, tj. variant. Obměny, neboli varianty statistického znaku jsou navzájem různé hodnoty statistického znaku. Statistický znak, který nabývá v daném statistickém souboru pouze jedné obměny, se nazývá shodný, např. statistický znak „ročník studia“ nabývá v statistickém souboru studentů druhého ročníku Vysoké školy finanční a správní pouze jedné obměny, tj. 2. Statistický znak nabývající pouze jedné obměny se nazývá identifikačním statistickým znakem, neboť je zpravidla součástí definice daného statistického souboru. Statistické znaky, které nabývají v uvažovaném statistickém souboru více než jedné obměny, nazýváme proměnné. Proměnné jsou předmětem statistického zkoumání.
1.2.1 Typy proměnných
Z hlediska toho, jsou-li obměny určité proměnné vyjádřeny slovně nebo číselně, rozdělujeme proměnné na slovní proměnné, které se občas rovněž nazývají alfabetické, častěji však kategoriální, a dále na číselné proměnné, které se mezinárodně nazývají numerické. Někdy se můžeme setkat především ve starší odborné literatuře s členěním na kvalitativní znaky, které odpovídají slovním proměnným, a kvantitativní znaky, které odpovídají číselným proměnným.
Jako příklad slovní proměnné lze uvést druh vlastnictví bytu 40 náhodně vybraných domácností s obměnami: nájemní, vlastní, družstevní. Jako příklad číselné proměnné můžeme uvést počet členů domácnosti nebo třeba měsíční výdaje domácnosti. Dalším příkladem slovní proměnné může být v souboru vysokoškolských studentů výsledek zkoušky ze statistiky s obměnami: výborně, velmi dobře, dobře a nevyhověl. Slovní proměnné se někdy snažíme převést na proměnné číselné, tak např. slovní proměnnou výsledek zkoušky ze statistiky můžeme převést na číselnou proměnnou známka ze statistiky s obměnami: 1, 2, 3 a 4. K převodu některých slovních proměnných na proměnné číselné nás vede povaha některých statistických postupů spočívajících ve zkoumání zákonitostí hromadných jevů pomocí čísel. U některých slovních proměnných není možný převod na numerické proměnné, např. druh vlastnictví bytu.
Z hlediska toho, kolika obměn proměnné v daném statistickém souboru nabývají, členíme proměnné na alternativní proměnné, které nabývají pouze dvou obměn, a množné proměnné, které nabývají více než dvou obměn.
Jako příklad alternativní proměnné ve statistickém souboru zaměstnanců určitého podniku můžeme uvést pohlaví s obměnami muž a žena. Slovní alternativní proměnná se často převádí na číselnou alternativní proměnnou tím způsobem, že se jedna z obou obměn této proměnné označí číslem 1 a druhá z obou obměn dané proměnné se označí číslem 0. Jedničkou se obvykle označí ta z obou obměn, která nás v dané souvislosti více zajímá. Slovní alternativní proměnnou, která je uvedeným způsobem převedena na číselnou alternativní proměnnou, nazýváme nulajedničkovou veličinou. Příkladem množné proměnné ve statistickém souboru zaměstnanců určitého podniku může být věk zaměstnance v dokončených letech nebo počet dětí zaměstnance.
Z hlediska toho, zda obměny číselné proměnné mohou nabýt v určitém intervalu, v němž se reálně pohybují, všech reálných čísel nebo jen izolovaných číselných hodnot, se číselné proměnné dále člení na nespojité proměnné, někdy říkáme diskrétní proměnné, které mohou nabývat v určitém intervalu pouze izolovaných číselných hodnot, nejčastěji jsou to přirozená čísla nebo nezáporná celá čísla, a spojité proměnné, někdy říkáme kontinuální proměnné, které mohou nabývat v daném intervalu jakýchkoliv reálných číselných hodnot. Členění proměnných na nespojité a spojité se týká, jak již bylo uvedeno, pouze číselných proměnných.
Příkladem nespojité proměnné ve statistickém souboru zaměstnanců určitého podniku může být počet dětí zaměstnance s obměnami: 0, 1, 2,..., příkladem spojité proměnné ve statistickém souboru zaměstnanců určitého podniku může být hrubý měsíční příjem zaměstnance. Členění číselných proměnných na nespojité a spojité je do určité míry relativní a subjektivně ovlivnitelné. Například ve statistickém souboru zaměstnanců určitého podniku bude číselná proměnná věk proměnnou spojitou (nikomu není v daném okamžiku přesně 20, 21, 22 atd. ale třeba 22,248...4 let), ale číselná proměnná věk v dokončených letech bude proměnnou nespojitou.
Z hlediska typu vztahů mezi obměnami členíme proměnné na nominální proměnné, neboli jmenné proměnné, názvové proměnné, u jejichž obměn nelze objektivně jednoznačně stanovit jediné pořadí tak, aby obměna s vyšším pořadím vyjadřovala vyšší stupeň sledované vlastnosti, než jiná obměna s pořadím nižším, tj. o dvou obměnách nominální proměnné můžeme pouze říci, zda jsou stejné nebo různé, nic více; na ordinální proměnné, neboli pořadové proměnné, o jejichž obměnách lze nejen konstatovat, že jsou různé, ale rovněž je lze jednoznačně seřadit od nejnižší obměny po nejvyšší a rozdíl dvou obměn ordinální proměnné značí pouze rozdíl v pořadí těchto obměn; a na metrické proměnné, neboli měřitelné proměnné, to jsou ty proměnné, u kterých lze o dvou obměnách říci nejen, že jsou různé a že jedna z těchto obměn je větší než druhá, ale i změřit, o kolik je jedna obměna větší než druhá. Metrické proměnné jsou vždy proměnné číselné. Pro metrické proměnné se často používá souběžně název kardinální proměnné, ale uvedené ztotožnění metrických a kardinálních proměnných není přesné, neboť kardinální proměnná je taková metrická proměnná, která nabývá v určitém statistickém souboru pouze kladných číselných obměn. O dvou obměnách kardinální metrické proměnné lze říci nejen, o kolik je jedna obměna větší než druhá, ale rovněž, kolikrát je jedna obměna větší než druhá.
Jako příklad nominální proměnné ve statistickém souboru zaměstnanců určitého podniku můžeme uvést místo narození nebo druh absolvované střední školy. Příkladem ordinální proměnné ve statistickém souboru zaměstnanců určitého podniku může být nejvyšší dosažené vzdělání. Příkladem ordinální proměnné v souboru vysokoškolských studentů může být výsledek zkoušky ze statistiky s obměnami: výborně, velmi dobře, dobře a nevyhověl nebo známka ze statistiky s obměnami: 1, 2, 3 a 4. Příkladem metrické proměnné v souboru zaměstnanců určitého podniku může být hrubý měsíční příjem.
Z hlediska oboru obměn, kterých může v daném souboru metrická proměnná nabýt, členíme metrické proměnné na kardinální metrické proměnné a nekardinální metrické proměnné, které nabývají v daném statistickém souboru kladných i nekladných číselných obměn. U dvou obměn nekardinální metrické proměnné lze pouze změřit, o kolik je jedna obměna větší než druhá, ale nelze říci, kolikrát je jedna kladná obměna větší než jiná obměna nekladná. Příkladem nekardinální metrické proměnné může být ve statistickém souboru vysokoškolských studentů měsíční stipendium studenta, neboť tato proměnná může kromě kladných hodnot nabývat i hodnoty 0.
1.2.2 Statistická šetření
Předmětem zájmu jsou některé vlastnosti určitých statistických souborů. Tyto vlastnosti jsou vyjádřeny určitými proměnnými, které nabývají u každé statistické jednotky určité hodnoty. Ke statistickému zkoumání jsou zapotřebí právě tyto hodnoty, neboli data či údaje. Tato data lze získat dvojím způsobem. Nejčastěji je odněkud převezmeme, např. z některé statistické ročenky. Sekundárními daty označujeme převzaté hodnoty proměnných, které nás zajímají. Méně často získáváme potřebná data tak, že je sami zjišťujeme. Jedná se pak o primární data.
Získávání neznámých statistických dat o hodnotách proměnných jednotlivých statistických jednotek nazýváme statistické šetření, tj. statistické zjišťování. Kromě vlastního získávání statistických dat jsou náplní statistického šetření i teoretické a praktické postupy takovéhoto šetření. Účelem statistického šetření je získání statistických dat potřebných k prozkoumání nebo sledování nějakých hromadných jevů či jejich vztahů nebo jejich vývoje. Z konkrétního účelu statistického šetření plyne, které proměnné se mají zjišťovat, co bude statistickým souborem a co statistickou jednotkou. Ke splnění konkrétního účelu statistického šetření je třeba velmi přesné věcné, prostorové a časové vymezení statistického souboru a příslušných proměnných.
Z hlediska časového vymezení nás zajímá rozhodný okamžik, což je časový moment určující pro zahrnutí či nezahrnutí statistických jednotek do statistického souboru a pro zachycení hodnot okamžikových statistických znaků, a rozhodná doba, což je časový interval o určité konečné délce, jehož obě hranice jsou vymezeny dvěma časovými okamžiky nebo počátečním časovým okamžikem a délkou tohoto období. Tento časový interval je potřebný v případě intervalového statistického znaku (např. měsíční kapesné studenta v Kč).
Z hlediska toho, zda jsou zjišťovány hodnoty sledovaných proměnných u všech statistických jednotek základního souboru nebo pouze u některých jednotek základního souboru rozdělujeme statistická šetření na vyčerpávající a nevyčerpávající statistická šetření.
Vyčerpávající statistická šetření jsou taková statistická šetření, při kterých zjišťujeme hodnoty příslušných proměnných u všech statistických jednotek základního statistického souboru. I při vyčerpávajícím statistickém šetření se však může stát, že se z nějakého důvodu nepodaří zjistit hodnoty zkoumaných proměnných u některých statistických jednotek, i když se to zamýšlelo. Jedná se tedy potom o statistické šetření, které není zcela úplné, ačkoliv bylo organizováno jako vyčerpávající statistické šetření a rovněž zůstává statistickým šetřením vyčerpávajícím. Úplné statistické šetření je takové statistické šetření, při kterém byly prošetřeny všechny statistické jednotky, které být prošetřeny měly. Pokud některé statistické jednotky, jejichž prošetření bylo zamýšleno, prošetřeny nebyly, jedná se o neúplné statistické šetření. Neúplnost vyčerpávajícího statistického zjišťování lze v některých případech tolerovat, a sice tehdy, je-li počet statistických jednotek, u kterých se nepodařilo zjistit hodnoty sledovaných proměnných, vzhledem k rozsahu základního souboru velmi malý. Výhodou úplného vyčerpávajícího statistického šetření je skutečnost, že poskytuje podklady pro zcela přesné charakterizování základního souboru, a skutečnost, že poskytuje hodnoty zkoumaných proměnných jednotlivě o každé statistické jednotce zvlášť. Nevýhodou je to, že někdy nelze vyčerpávající statistické šetření vůbec uskutečnit, a to tehdy, je-li šetření spojeno s likvidací statistických jednotek (zkoumání pevnosti vyrobených součástek, změření pevnosti je spojeno se zničením součástky). Nevýhodou vyčerpávajícího statistického šetření je i to, že je velice drahé, velmi časově náročné a vede k relativně dlouhé době, která je potřebná ke statistickému zpracování.
Nevyčerpávající statistická šetření jsou taková šetření, u kterých se předem počítá s tím, že hodnoty zkoumaných proměnných budou zjišťovány pouze u statistických jednotek výběrového statistického souboru. Nevyčerpávající statistické šetření může být opět úplné i neúplné. Hlavní výhodou nevyčerpávajícího statistického šetření je především to, že bývá jedinou alternativou v případech, kdy samotné zjišťování je spojeno se zničením statistických jednotek. Další výhodou nevyčerpávajících statistických šetření je skutečnost, že získání dat je poměrně úsporné na finanční, věcné a pracovní náklady a je možné snáze a rychleji zkontrolovat správnost a úplnost získaných výsledků. Při nevyčerpávajícím statistickém šetření lze registrační chyby, které vznikají při zaznamenávání, omezit na zanedbatelné minimum. Další výhodou nevyčerpávajícího statistického šetření je, že zpracování a vyhodnocování tohoto zjišťování je rychlejší. Hlavní nevýhodou nevyčerpávajícího statistického šetření je skutečnost, že odhady získané s využitím výběru se plně nekryjí se skutečnými vlastnostmi základního souboru, ale jsou zatíženy výběrovou chybou. Výběrová chyba vzniká proto, že hodnoty proměnných jsou zjišťovány pouze u výběrového statistického souboru a závěry jsou prováděny pro celý základní statistický soubor. Z hlediska toho, do jaké míry lze výsledky nevyčerpávajícího statistického šetření zobecnit, neboli rozšířit poznatky získané nevyčerpávajícím statistickým šetřením na základní soubor, členíme nevyčerpávající statistická šetření na nereprezentativní nevyčerpávající statistická šetření a reprezentativní nevyčerpávající statistická šetření.
V případě nereprezentativních nevyčerpávajících statistických šetření výběrový statistický soubor nereprezentuje, tj. nepředstavuje, dostatečně celý zkoumaný základní statistický soubor a možnost zobecnění poznatků získaných nereprezentativními nevyčerpávajícími statistickými šetřeními je problematická. Jako příklad takovýchto statistických šetření lze uvést anketu.
V případě reprezentativních nevyčerpávajících statistických šetření je výběrový statistický soubor svými vlastnostmi věrnou zmenšeninou vlastností základního statistického souboru a poznatky pořízené z prozkoumání vlastností výběrového statistického souboru je možné zobecnit na vlastnosti základního statistického souboru. Z hlediska způsobu zajištění reprezentativnosti se reprezentativní nevyčerpávající statistická šetření člení ještě na dva druhy, a to na záměrný výběr a na náhodný výběr. V případě záměrného výběru, neboli úsudkového výběru, zkušený odborník na základě známých vlastností základního statistického souboru a vlastního úsudku vybírá ze základního statistického souboru určité statistické jednotky záměrně tím způsobem, aby byl výběrový statistický soubor reprezentativní. V případě náhodného výběru, neboli pravděpodobnostního výběru, se reprezentativnost zabezpečuje prostřednictvím náhody.
1.3 Zpracování dat o slovní proměnné
Obměny slovní proměnné označíme ai, i = 1, 2,..., k, kde k je počet obměn uvažované slovní proměnné. Dále označíme absolutní četnosti ni, i = 1, 2,..., k, což znamená, že n 1 statistických jednotek statistického souboru má obměnu a 1, n 2 statistických jednotek statistického souboru má obměnu a 2 atd. až nk statistických jednotek statistického souboru má obměnu ak. Rozsah výběrového statistického souboru označíme n. Platí
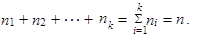
| (1.1) |
Obdobně označíme relativní četnosti pi, kde

| (1.2) |
tedy p 1 představuje relativní četnost jednotek, které mají obměnu a 1, p 2 představuje relativní četnost jednotek, které mají obměnu a 2, atd. až pk představuje relativní četnost jednotek, které mají obměnu ak. Platí

| (1.3) |
součet relativních četností je roven jedné. Jestliže vynásobíme relativní četnosti stem, získáváme relativní četnosti v procentech a jejich součet je tedy roven 100 %.






