Automobil dosáhl na celé trase průměrnou rychlost 71,292 km/h.
b) Opět x 1 = 60 km/h, x 2 = 70 km/h a x 3 = 80 km/h, přičemž tentokrát neznáme absolutní četnosti ni, i = 1, 2, , k, ale pouze četnosti relativní pi, i = 1, 2, , k, tj. p 1 = 0,1 (vzdálenost města A a města B tvoří 10 % trasy), p 2 = 0,4 (vzdálenost města B a města C tvoří 40 % trasy) a p 3 = 0,5 (vzdálenost města C a města D tvoří 50 % trasy). Trasy zůstávají tři, tedy k = 3. Vztah (1.25) je vyjádřen rovněž pomocí relativních četností
|
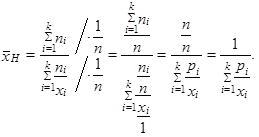
Do tohoto vztahu dosadíme
|
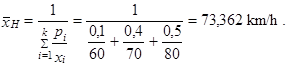
Na celé trase automobil dosáhl průměrné rychlosti 73,362 km/h.
Příklad 1.16
Při placení zboží platební kartou v hypermarketu byla v jednom okamžiku na dvanácti pokladnách měřena doba, během které pokladní ověří platnost platební karty zákazníka v bance. U sedmi zákazníků trvalo ověření tři minuty a u pěti zákazníku dvě minuty. Určete průměrnou dobu potřebnou k ověření platební karty.
Řešení:
U n 1 = 7 zákazníků trvalo ověření x 1 = 3 minuty a u n 2 = 5 zákazníků trvalo ověření x 2 = 2 minuty. Opět podíl
|
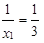
představuje, kolik zákazníků (jako desetinné číslo) bylo v průměru ověřeno za jednu minutu v prvním případě, takovýchto zákazníků je však n 1 = 7. Získáváme
|
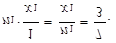
Obdobně pro druhý případ získáváme podíl
|
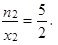
Opět, protože má smysl součet podílů
|
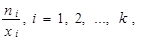
použijeme pro výpočet harmonický průměr. Hodnota x 1 = 3 je zde obsažena n 1 = 7 krát, hodnota x 2 = 2 je zde obsažena n 2 = 5 krát. Použijeme proto vzorec váženého harmonického průměru (1.25), máme dvě skupiny zákazníků, tedy k = 2
|
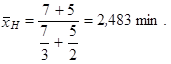
Průměrná doba potřebná k ověření platební karty je 2,483 min.
Cvičení
1. Určete aritmetický průměr následujícího souboru, který obsahuje spotřebu elektrické energie v jednotlivých kancelářních měsících, viz tabulka 1.28.
|
|
|
| Tabulka 1.28 | ||||||||||
2. Sledovaný statistický znak nabyl následujících hodnot, viz tabulka 1.29. Určete aritmetický průměr.
| Tabulka 1.29 | ||||||
3. V následující tabulce 1.30 jsou uvedeny koeficienty růstu produkce výrobního podniku A a výrobního podniku B v letech 2002 až 2006.
| Tabulka 1.30 | |||||
| Rok | |||||
| Podniky | |||||
| A | − | 1,1112 | 1,0017 | 0,9988 | 1.0555 |
| B | − | 1,3681 | 1,3642 | 0,7814 | 0,8802 |
Určete, který podnik má vyšší průměr z těchto koeficientů.
4. V následující tabulce 1.31 jsou uvedeny koeficienty nárůstu státního dluhu státu XSR a státu YSR v letech. 1994 až 2006
| Tabulka 1.31 | ||||||
| Stát | Stát | |||||
| Rok | XSR | YSR | Rok | XSR | YSR | |
| − 1,04 1,07 1,05 1,06 1,09 1,40 | − 1,10 1,20 1,09 0,95 0,98 0,99 | 1,23 1,12 1,14 1,09 1,10 1,01 | 1,01 1,05 1,06 1,70 1,60 1,30 |
Určete, který stát má vyšší průměr z těchto koeficientů.
5. Naměřené délky souběžně probíhajících výrobních operací jsou uvedeny v tabulce 1.32. Určete průměrnou dobu provedení jedné operace.
| Tabulka 1.32 | ||||||
| 15,7 | 17,6 | 12,3 | 14,1 | 16,7 | 11,2 | 21,3 |
| 14,7 | 14,6 | 11,5 | 18,1 | 11,9 | 16,7 | 20,3 |
6. Naměřené délky souběžně odbavovaných turistů na letišti jsou uvedeny v tabulce 1.33. Určete průměrnou dobu odbavení jednoho turisty.
| Tabulka 1.33 | ||||||
| 8,7 | 6,2 | |||||
| 7,5 | 5,6 | 8,2 | 6,7 | |||
| 5,7 | 7,3 | 6,9 | 4,1 | 16,3 | 4,2 | 15,7 |
| 4,7 | 4,6 | 10,1 | 8,9 | 9,9 | 4,7 | 20,0 |
Výsledky
1.
162,523
2.
106,571
3.
Podnik B (1,0644) má vyšší koeficient než podnik A (1,0408)
4.
YSR (1,1486) má vyšší koeficient než XSR (1,1125)
5.
14,88
6.
7,81
Charakteristiky variability
Obrázek 1.17
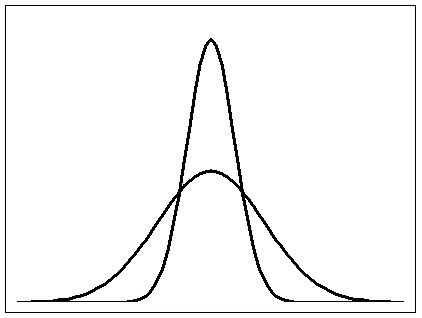
Hodnoty statistického souboru A jsou těsněji koncentrovány okolo aritmetického průměru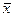 
než hodnoty statistického souboru B, můžeme proto konstatovat, že v případě statistického souboru A aritmetický průměr lépe vystihuje polohu statistického souboru, nežli je tomu v případě statistického souboru B. Vypovídací schopnost aritmetického průměru je tím větší, čím je menší variabilita sledované proměnné a naopak.
|
|
|
Číselná proměnná je vždy variabilní na rozdíl od konstanty, jejíž variabilita je nulová. Malý stupeň variability, tj. stupeň variability blízký nulové variabilitě, představuje malou vzájemnou odlišnost hodnot sledované proměnné, a tedy velkou vzájemnou podobnost hodnot dané proměnné, což znamená, že průměr, medián i modus jsou dobrými charakteristikami obecné velikosti hodnot sledované proměnné ve statistickém souboru. Vysoký stupeň variability představuje velkou vzájemnou odlišnost hodnot sledované proměnné, což znamená, že vypočítané charakteristiky polohy, jako jsou průměr, medián i modus, nejsou dobrými charakteristikami obecné výše hodnot sledované proměnné ve statistickém souboru.
Charakteristik variability existuje celá řada, nulová hodnota charakteristik variability značí konstantnost, neboli nulovou variabilitu. Kladné hodnoty charakteristik variability značí vyšší stupeň variability.
Charakteristiky měřící proměnlivost statistického souboru v absolutní velikosti označujeme jako charakteristiky absolutní variability. Takovéto charakteristiky vyjadřují variabilitu ve stejných měrových jednotkách, ve kterých je vyjádřena sledovaná proměnná (nebo např. ve čtvercích těchto měrových jednotek). Srovnáváme-li variabilitu statistických souborů, které se liší svojí polohou, používáme charakteristiky relativní variability. Tyto charakteristiky vyjadřují variabilitu sledované proměnné v poměru k poloze sledované proměnné ve statistickém souboru. Takovéto charakteristiky jsou bezrozměrná čísla (nebo po vynásobení stem v procentech), což umožňuje rovněž srovnání variability proměnných, které se liší měrovou jednotkou.
Charakteristiky absolutní variability
Variační rozpětí
Variační rozpětí číselné proměnné x je definováno jako rozdíl mezi maximální hodnotou proměnné xmax a minimální hodnotou proměnné xmin
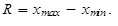
| (1.31) |
Variační rozpětí představuje pouze velice přibližnou charakteristiku variability hodnot číselné proměnné z toho důvodu, že je příliš ovlivněno velikostí extrémních hodnot. Výskyt jediné extrémní hodnoty proměnné vyvolá značnou velikost variačního rozpětí. Variační rozpětí dále nic neříká o variabilitě hodnot sledované proměnné uvnitř variačního rozpětí.
|
|
|
Kvantilová rozpětí
Kvartilové rozpětí číselné proměnné x je definováno jako rozdíl mezi horním kvartilem proměnné a dolním kvartilem proměnné
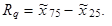
| (1.32) |
Podobně je dále definováno decilové rozpětí jako
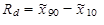
| (1.33) |
a percentilové rozpětí jako
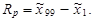
| (1.34) |
Kvantilová rozpětí při charakterizování variability neberou v úvahu velikost všech hodnot číselné proměnné.
Rozptyl
Prostý rozptyl n hodnot x 1, x 2,..., xn, které nemusí být uspořádány, je definován jako aritmetický průměr čtverců odchylek jednotlivých hodnot sledované proměnné od jejich aritmetického průměru
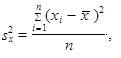
| (1.35) |
jsou-li hodnoty proměnné setříděny do tabulky rozdělení četností, lze použít vážený rozptyl
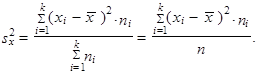
| (1.36) |
Jestliže při výpočtu váženého rozptylu (1.36) použijeme namísto absolutních četností n 1, n 2,..., nk četnosti relativní p 1, p 2,..., pk, získáváme
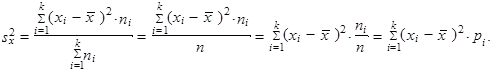
| (1.37) |
Častěji než rozptyl (1.35) až (1.37) je prostý rozptyl n hodnot x 1, x 2,..., xn, které opět nemusí být uspořádány, definován jako
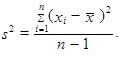
| (1.38) |
Jsou-li hodnoty proměnné již setříděny do tabulky rozdělení četností, použijeme raději vážený rozptyl
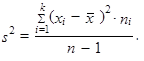
| (1.39) |
Použijeme-li při výpočtu váženého rozptylu (1.39) místo absolutních četností n 1, n 2,..., nk relativní četnosti p 1, p 2,..., pk, dostaneme
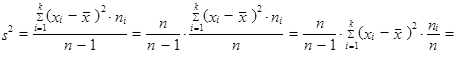
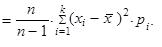
| (1.40) |
Rozptyl (1.38) až (1.40) označujeme jako výběrový rozptyl.
Rozdíl mezi rozptyly
|
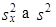
při velkém rozsahu výběru (n > 30) je zanedbatelný. Např. ze vztahů (1.35) a (1.38) plyne
|
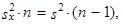
odtud získáváme
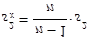
| (1.41) |
a
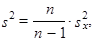
| (1.42) |
tj. z rozptylu
|
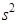
získáme násobením koeficientem
|
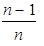
rozptyl
|
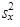
a z rozptylu
|
|
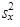
získáme násobením koeficientem
|
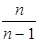
rozptyl
|
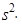
Je-li nutné symbolicky rozlišit rozptyl základního souboru a rozptyl výběrového souboru, tak rozptyl základního souboru označujeme zpravidla s2 a rozptyl výběrového souboru s 2.
Rozptyl má některé důležité vlastnosti:
| 1. | Rozptyl konstanty se rovná nule | ||
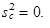
| (1.43) | ||
| 2. | Součet čtverců odchylek jednotlivých hodnot sledované proměnné od jejich aritmetického průměru (čitatel rozptylu) je vždy menší než součet čtverců odchylek jednotlivých hodnot sledované proměnné od libovolné konstanty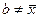 
| ||
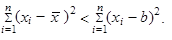
| (1.44) | ||
| 3. | Přičteme-li ke všem hodnotám, resp. odečteme-li od všech hodnot, proměnné libovolnou kladnou konstantu (a > 0), rozptyl se nezmění | ||
| |||
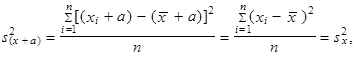
| resp. | (1.45) | ||
| |||
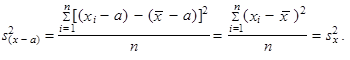
| 4. | Násobíme-li, resp. vydělíme-li, všechny hodnoty proměnné libovolnou nenulovou konstantou (k ≠ 0), rozptyl se znásobí, resp. vydělí, čtvercem této konstanty | ||
| |||
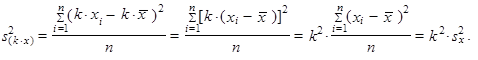
| resp. | (1.46) | ||
| |||
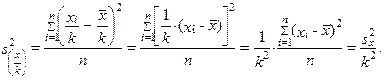
| 5. | Rozptyl (1.35) až (1.37) můžeme vyjádřit jako aritmetický průměr čtverců hodnot sledované proměnné zmenšený o čtverec aritmetického průměru hodnot dané proměnné | ||
| |||
| |||
| |||
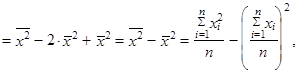
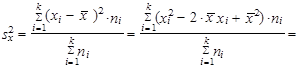
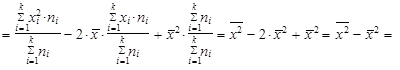
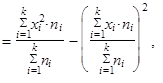
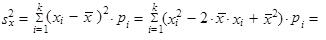
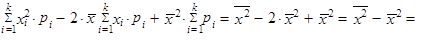
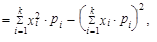
| takže platí | |||
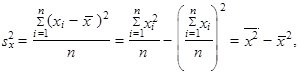
| (1.47) | ||
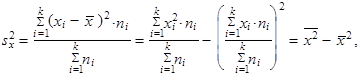
| (1.48) | ||
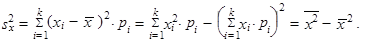
| (1.49) | ||
| Vztahům | |||
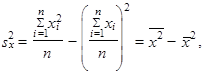
| (1.50) | ||
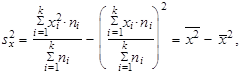
| (1.51) | ||
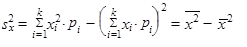
| (1.52) | ||
| říkáme výpočtový tvar rozptylu. | |||
| 6. | Rozptyl součtu dvou číselných proměnných x a y je roven součtu rozptylů obou těchto proměnných, ke kterému přičteme dvojnásobek kovariance | ||
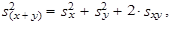
| (1.53) | ||
| rozptyl rozdílu dvou číselných proměnných x a y je roven součtu rozptylů obou těchto proměnných, od kterého odečteme dvojnásobek kovariance | |||
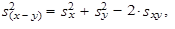
| (1.54) | ||
| kde | |||
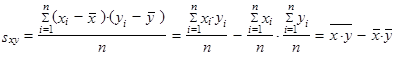
| (1.55) | ||
| je kovarianceproměnných x a y, která charakterizuje vzájemnou závislost těchto proměnných. | |||
| 7. | Je-li statistický soubor rozdělen na k dílčích podsouborů s dílčími rozptyly v jednotlivých dílčích podsouborech | ||
| |||
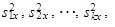
| s dílčími aritmetickými průměry v jednotlivých dílčích podsouborech | |||
| |||
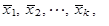
| a s počty pozorování v jednotlivých dílčích podsouborech n 1, n 2,..., nk, rozptyl celkového statistického souboru vypočteme jako součet aritmetického průměru dílčích rozptylů a rozptylu dílčích aritmetických průměrů | |||
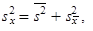
| (1.56) | ||
| kde | |||
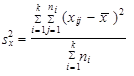
| (1.57) | ||
| je celkový rozptyl statistického souboru (celková variabilita), | |||
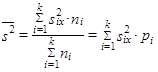
| (1.58) | ||
| je aritmetický průměr dílčích rozptylů (vnitroskupinová variabilita) a | |||
| |||
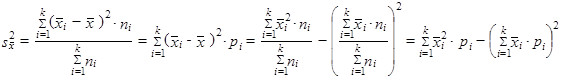
| (1.59) | |||
| je rozptyl dílčích aritmetických průměrů (meziskupinová variabilita). | |||
S využitím vztahu (1.56) můžeme vypočítat celkový rozptyl (1.57), i když neznáme původní hodnoty číselné proměnné. Výše uvedený rozklad celkového rozptylu (1.57) na aritmetický průměr dílčích rozptylů (1.58) a rozptyl dílčích aritmetických průměrů (1.59) umožňuje rovněž posoudit, do jaké míry je celkový rozptyl ovlivněn variabilitou uvnitř skupin (vnitroskupinová variabilita) a do jaké míry variabilitou mezi skupinami (meziskupinová variabilita).
|
|
|
|
|
|
