А) общественное обращение постоянного капитала, переменного капитала и прибавочной стоимости 17 страница

Сумма стоимости предметов потребления общества оста­лась вообще неизменной. Лишь большая ее часть произведена в форме предметов потребления рабочих, а меньшая — в форме предметов потребления капиталистов. В действительности необ­ходимые жизненные средства образуют как часть I b, так и часть I a. Но весьма «значительная часть lb состоит из предме­тов роскоши. При изменившемся распределении большая часть общественного фонда потребления находится в форме необходи­мых жизненных средств₁ меньшая часть — в форме предметов роскоши.

Наконец, что касается денежного капитала, в виде кото­рого авансируется переменный капитал, то в случае V = M он был равномерно распределен между I a и I b. Теперь 1) аван­сируется меньше денежного капитала на V в I b, чем в I a и в абсолютных величинах в I b меньше, чем прежде. М_а и т. д. должна быть меньше, чем V_a и т. д., так как V > M; но М_а = = V_b и т. д. Следовательно, теперь авансированный в I b де­нежный капитал должен быть меньше в абсолютном выраже­нии, чем когда V = M.

Однако авансированный в I a и т. д. денежный капитал (на V_a и т. д.) должен в большей степени возрасти, нежели аван­сированный в I b и т. д. денежный капитал уменьшился. Так как V_α + V_αα + V_α + V_b + V _ßß + V _ß теперь больше (на ⅓, чем прежде, поскольку I a возрос с 300 до 400), a V_b, V _ßß, V _ß — меньше, чем прежде, то V_a + V_αα + V_α должны возрасти

К. МАРКС

не настолько, насколько уменьшается V_b, V _ßß, V_ß, а больше. Иначе I a не будет больше, чем I a в случае V = М.

[194] Раньше было: авансированный в качестве переменного денежный капитал — 300 ф. ст., прибавочная стоимость — 75 ф. ст., [всего] — 375 ф. ст.; теперь: переменный денежный капитал — 400 ф. ст., прибавочная стоимость — 37 ф. ст., все­го — 437 ф. ст.; то есть переменный капитал теперь на 100 ф. ст. больше.

В действительности (не говоря уже о том, что здесь вооб­ще взяты слишком большие по отношению к стоимости то­вара обращающиеся суммы: так, отношение денег, обращающих прибавочную стоимость, к деньгам, обращающим V, принято слишком малым), хотя С_а и т. д. = (V + М) (IIαα, IIα), тем не менее также и внутри IIα, IIαα и т. д. постоянно будут находиться деньги в качестве запаса для обращения приба­вочной стоимости, прежде чем I a купит постоянный капитал у IIαα, IIα. Однако более подробно об этом — впоследствии.

Если I a > I b, то при всех обстоятельствах требуется боль­ше денег для обращения V и меньше денег для обращения М. Часть денег, которая прежде служила средством обращения прибавочной стоимости, служит теперь средством обращения заработной платы и принимает поэтому форму денежного ка­питала.

Следовательно, если требуется больше денег для обраще­ния V, то значительная часть из них во всяком случае достав­ляется за счет тех денег, которые стали избыточными для обра­щения прибавочной стоимости.

Когда же отсутствует такой избыток, то он — при чисто металлическом обращении — образуется за счет приведения в текучее состояние лежащих праздно сокровищ.

При этом изменившемся распределении речь идет не только,, как показано, о просто измененном распределении имеющегося в наличии фонда потребления, или части годового продукта общества, которая входит в его фонд потребления. Так это обычно представляют себе. Речь идет об измененном распре­делении в формах фонда потребления, о потребительных фор­мах, в которых он существует, об измененном распределении рабочей силы в различных сферах производства, наконец — об измененном распределении постоянного капитала.

Итак, посредством такого изменения в вышеуказанном слу­чае I a увеличился бы с 300 до 400, то есть на ⅓, или на 33⅓%. Авансированный постоянный капитал остался бы преж­ним (по стоимости). Масса примененного труда осталась бы прежней. Авансированный переменный капитал возрос бы, —

ВТОРАЯ КНИГА. ПРОЦЕСС ОБРАЩЕНИЯ КАПИТАЛА

что, однако (поскольку мы рассматриваем лишь его матери­альный субстрат), не означает ничего иного, кроме того, что большая часть фонда потребления приняла бы форму предметов потребления рабочих, а меньшая — форму предметов потреб­ления капиталистов.

Если бы тот же результат достигался вследствие накопле­ния капитала, то (при неизменной пропорции V: М):

Первоначально капитал, равный 1 500 ф. ст. = С^{1 200} + V ³⁰⁰, производит 300 М. Следовательно, если бы V возрос с 300 до 400, то так же возросла бы и М, и мы имели бы:

Капитал был бы теперь: С ¹⁶⁰⁰ + V ⁴⁰⁰ + М ⁴⁰⁰. Или капитал возрос бы с 1 500 до 2 000, то есть на V₃ = 33⅓%.

Рост капитала на ⅓ огромен и требует времени, не говоря о том, что это сопровождалось бы обстоятельствами и движе­ниями, которые заставили бы сомневаться, не хуже ли теперь обстоят дела у рабочей силы, представленной V ⁴⁰⁰, чем они были прежде у рабочей силы, представленной V ³⁰⁰.

Механизм буржуазного общества способствует тому, что та­кие изменения, как, например, представленные в случае I (V = M) и II (V > Μ) (например, V_a = 2М_а) (стр. 191 *), сопровождают­ся обстоятельствами, парализующими их действие и даже их исключающими.

Итак, если мы сравниваем I (V = М) и IIα (V = 2 М), то это предполагает одновременное повышение заработной платы на ⅓ во всех отраслях производства.

Бόльшая часть продуктов I а (здесь мы сначала абстраги­руемся от внешней торговли) состоит из продуктов питания, которые должны быть произведены на один год вперед, — по крайней мере, в виде сырых материалов для производства продуктов питания. Спрос на них очень сильно возрастает. Прибыль в Ι a и т. д. соответственно пока тоже сильно возра­стает. Короче говоря, капитал и рабочая сила должны быть извлечены из I b и т. д. и перейти в Ι a и т. д. Это изменение сопровождается помехами в I b и т. д. Во-первых, падающим спросом на значительную часть этого продукта (так как лишь относительно небольшая часть его превращается из продукта I b в продукт Ι a, то есть покупается теперь рабочими вместо капиталистов). Поскольку это имеет место, постольку это означает простое перемещение того же самого продукта (и ка-

• См. настоящий том, стр. 272. Ред.

К. МАРКС

питала и рабочих, которые его производят) из I b в I a. Он просто учитывается не в одном классе, а в другом, потому что M уменьшается и в новых условиях в I b и т. д. наступает перепроизводство. Это падение сказывается на занятости ра­бочих в I b и т. д. Их заработная плата снижается, вместо того чтобы возрасти, в той мере, в какой их перевод в I а про­исходит не столь быстро, как их высвобождение в I b и т. д. (а их перевод отчасти затруднен из-за их принадлежности оп­ределенному предприятию в силу определенного разделения труда). С другой стороны, падение их заработной платы будет сдерживать рост спроса в самом I a. Итак, возникает внезап­ное изменение, которое, по крайней мере частично, парализует указанное изменение.

Продукт I b и т. д. состоит отчасти из необходимых жиз­ненных средств и т. д., которые потребляются челядью капи­талистов, слугами и т. д., — короче говоря, непроизводитель­ными работниками. Часть из них увольняют при падении M на ⅓. (Однако если рассматривать совокупный класс капита­листов, то есть всех, кому принадлежит прибавочная стоимость, то это не имело бы такого значения, как может пока­заться на первый взгляд. Сравни английские отчеты о наро­донаселении за 1861 год ⁵¹.) Часть уволенных — дети рабо­чих и т. д. — могла бы с возрастом быть использована самими их родителями разумнее, чем в качестве прислуги и т. д.: они поступают на рынок рабочей силы, а именно — на рынок рабочей силы I а и т. д. Это прежде всего было бы просто ком­пенсацией за то, что часть излишних в I b рабочих здесь вла­чит жалкое существование. Короче говоря, если учесть, что, с одной стороны, класс капиталистов может наблюдать за де­лом, а, с другой стороны, высвобождение применяемых в I b производительных рабочих и части непроизводительных работ­ников, участвующих в потреблении продукта I b, может вызы­вать реакцию против самого процесса, — то становится по­нятной трудность и относительная невозможность изменений таким путем. Именно — при принятых предположениях, что производительность, интенсивность и продолжительность ра­бочего дня остаются прежними. При этом не упомянута реак­ция, которую вызывает повышение заработной платы в при­менении машин и т. д., то есть средств дальнейшего высвобож­дения рабочей силы.

Это — имманентные механизму капиталистического произ­водства препятствия на пути любого быстрого и всеобщего изменения этого рода; и если изменение является лишь по­степенным и частичным, то только накапливаются препят-

ВТОРАЯ КНИГА. ПРОЦЕСС ОБРАЩЕНИЯ КАПИТАЛА 283

ствия, которые капиталистическое производство стихийно со­здает против подобного изменения, — те препятствия, которые буржуазные экономисты зачастую рассматривают как до­казательство того, что дело вообще невозможно. Отсюда лишь следует, что необходимы всеобщие меры, которые затрудняют действие нашего стихийного механизма, и если они и не могут преобразовать его тотчас же, то вызывают внезапные значитель­ные изменения, которые подрывают, ослабляют имманентную ему силу сопротивления и вследствие этого облегчают даль­нейшие изменения в том же направлении.

Если теперь мы сравним III (V < М) со II и I, то здесь имеют место обратные явления, или изменения в противо­положном направлении.

[195] I Ь > I а. V < M во всех сферах производства. В I b производится большая масса прибавочной стоимости, чем в I a. I b поглощает больше рабочей силы, чем I a. Постоянного капи­тала больше поглощается в 1 b, чем в I a.

Что касается авансированного переменного денежного ка­питала, то он равен 250 ф. ст. (а не так, как в I случае, 300, и не так, как во II случае, 400). Кроме того, для обращения прибавочной стоимости необходимо, если исходить из старого масштаба, 34²/₁₈ + 68¹/_l8 = 102³/₁₈ = 102¹/₆, скажем, 103 ф. ст. Вся сумма обращающихся денег равна 353 ф. ст.

* * *

Рабочий фонд. Прежде всего следует отметить: здесь — распространенный взгляд на фиксированность так называе­мого рабочего фонда. При одной и той же величине стоимости годового общественного продукта этот рабочий фонд может быть равен 300, 400, 350, 250 и т. д. Он может упасть на­много ниже стоимости рабочей силы — вплоть до абсолютного минимума, и он может возрасти и стать больше последнего и т. д., — возможны самые различные вариации. Но то, что он есть фиксированная величина, является одной из основных догм политической экономии!

If) Абстрактные предпосылки исследования обращения

и воспроизводства общественного капитала

и действительный процесс]

Спрашивается, прежде всего, в какой мере изложенное до сих пор покоится не на чисто абстрактных и противореча­щих действительности предположениях?

К. M A P К С

Ясно, что такого абстрактного разделения на I a и т. д. — производство предметов потребления рабочих — и I b и т. д. — производство предметов потребления капиталистов — в дей­ствительности не существует.

Необходимые жизненные средства образуют, конечно, наи­более значительную часть предметов потребления рабочих. Но они в значительной мере входят также и в потребление капиталистов. Очень значительная часть продуктов питания идентична и для тех, и для других. Так же топливо. Во всем остальном, даже если это продукты одной и той же катего­рии — жилище, одежда, меблировка и т. д., — то все же это продукты разного рода. С другой стороны, в потребление ра­бочих входят также некоторые предметы роскоши (хотя на­верняка это не так, если брать среднюю для всего класса и взвесить, например, то, как много тратится на водку и т. д, и как мало — на пищу, одежду для детей и т. д.).

Большая часть постоянного капитала — та же самая, сырые материалы, машины, орудия, здания и т. д. Там, где различны станки, там одни и те же постройки, двигатели и передаточ­ные механизмы и т. д. Это в действительности доказывает, что перевод постоянного капитала из I a в I b и vice versa * связан с гораздо меньшими трудностями, чем перевод рабочих сил, ставших односторонне развитыми вследствие разделения труда.

Противоречит ли это изложенным законам?

Прежде всего, остается большое различие в вещественном образе, потребительной форме фонда I a и фонда I b. Первый состоит в своей большей части из необходимых жизненных средств, второй — в очень значительной части из предметов роскоши, то есть из продуктов, которые при данном разви­тии производительной силы и данной рабочей силе отчасти вовсе не производились бы, отчасти производились бы в садом небольшом размере, если бы производители были в то же вре­мя и потребителями своего продукта.

Поскольку рассматривается общая схема, постольку ка­жется, что наибольшая трудность возникает из того, что один и тот же капиталист принадлежит и категории I а, и катего­рии I b. Например, капиталистический земледелец производит хлеб, который входит как в фонд потребления I а, так и в фонд потребления I b. Следовательно, часть прибавочной стоимости, производимой в I а, потребляется самим ее капиталистическим производителем в I а, и ее не нужно сначала превращать из на­туральной формы I a в натуральную форму I b. Следовательно,

* — обратно. Ред.

ВТОРАЯ КНИГА. ПРОЦЕСС ОБРАЩЕНИЯ КАПИТАЛА 285

часть М_аа (соответственно M_a) не нужно стачала реализовывать в I b и т. д., и вследствие этого М_а не должна быть обязательно равна V и т. д. (I b и т. д.).

Лучше всего все-таки рассмотреть найденные законы во всеобщей форме и посмотреть, насколько они связаны с опре­деленной формой схемы — или, вернее, позволяет ли данная форма выступить отчетливее этим законам.

I) Согласно схеме (например, I V = М) (стр. 191 *), стои­
мость фонда потребления рабочих равна цене общественной ра­
бочей силы, которая была применена во всех отраслях про­
цесса производства. (В данном случае она равна V (а, αα, α) +
+ V (b, ßß, ß).) С другой стороны, стоимость фонда потребле­
ния капиталистов равна сумме произведенной во всех отрас­
лях прибавочной стоимости. Поэтому сумма стоимости про­
дуктов, предназначенных для индивидуального потребления,
равна сумме стоимости затраченного обществом переменного
капитала V (а, αα, α + b, ßß, ß) + M (а, αα, α + b, ßß, ß),
то есть равна стоимостному продукту годовых общественных
рабочих дней.

Это положение абсолютно не зависит от того, что I а и т. д. и I b и т. д. рассматриваются как два самостоятельных отдель­ных больших подразделения общественного процесса произ­водства, как это было в схеме.

Каков бы ни был материальный образ потребительной стоимости общественного фонда потребления, а следователь­но, и особенных процессов производства, из которых выходят конституирующие этот фонд элементы, его стоимость рав­на V + M, где V — цена всей примененной рабочей силы,, равная стоимостному продукту необходимой части рабочего дня, M — сумма прибавочной стоимости, равная стоимостному продукту затраченного прибавочного труда, а V + M равны стоимостному продукту годового общественного рабочего дня.

II) Точно так же ясно, что если весь фонд потребления ра­
вен, например, 600 (как в вышеуказанном случае) и если эти 600
разлагаются соответственно своим стоимостным составным ча­
стям на С ⁴⁰⁰ + V ¹⁰⁰ + М ¹⁰⁰, то содержащаяся здесь постоян­
ная часть капитала, С ⁴⁰⁰, должна быть [равна] (V_II + М _II ) ⁴⁰⁰,
произведенным в сферах производства, которые доставляют —
прямо или косвенно — средства производства товаров, образую­
щих фонд потребления. Эти С ⁴⁰⁰ (I) в виде предметов потреб­
ления должны быть обменены на (V_II + М_II) в виде средств
производства.

• См. настоящий том, стр. 272. Ред.

К. МАРКС

Это следует просто уже из того, что стоимость фонда по­требления разлагается на (V + М) всех отраслей производства.

Следовательно, стоимость фонда потребления равна V ₃₀₀+ + M ₃₀₀, где V ₃₀₀есть V всех классов и М ₃₀₀— M всех классов.

Далее, стоимость этого фонда потребления равна С_I ⁴⁰⁰ + + V_I ⁴⁰⁰+ M_I ¹⁰⁰. Здесь мы обозначаем через C_I постоянную часть капитала в стоимости фонда потребления; далее,_; V_I и M_I — созданная в самой сфере производства предметов по­требления стоимость V и М.

[196] Следовательно, так как C_I ⁴⁰⁰ + V_I ¹⁰⁰ + M_I ¹⁰⁰= V ³⁰⁰ + + M ³⁰⁰, то С_I ⁴⁰⁰(= V ³⁰⁰ + M ³⁰⁰) — (V_I ¹⁰⁰ + M_I ¹⁰⁰ ), a именно,

Следовательно, С_I ¹⁰⁰ = (V_x + M_x)⁴⁰⁰, то есть стоимость по­стоянной капитальной части предметов потребления равна стоимости переменной капитальной части плюс прибавочная стоимость средств производства.

Или вообще, если стоимость предметов потребления равна Т и это

Т = С_а + V_а + M_а (где С_а — постоянная часть капитала,

V_a — переменная, М_а — прибавочная стоимость этой сферы I),

то С _а = Т — (V _a + М _а), то есть равна (V_b + М_b), где V_b —

созданный во всех сферах, исклю­чая I a), V, a M_b — созданная во всех сферах, исключая I а),приба­вочная стоимость.

Теперь, далее, ясно, что С_а (здесь = C_I ⁴⁰⁰ ) должен сна­чала обменяться на (быть возмещен посредством) средства производства, входящие непосредственно в производство пред­метов потребления, или, другими словами, образующие нату­ральную форму постоянного капитала С_а, С_а как раз нужно вновь превратить из формы продукта — предметов потребле­ния — в его натуральную форму, то есть в средства произ­водства этого продукта, предметов потребления.

Поэтому если мы обозначим эти средства производства b₁, то С_а должен сначала быть возмещен этими средствами произ­водства b₁ той же стоимостью (то есть стоимость которых равна V_b + M_b). (Следовательно, в данном случае — товарами b₁ на сумму V_b + М_b = 400.)

Если бы теперь V + M в сфере b₁ были равны V_b + M_b, то есть равны сумме производимых вообще вне сферы Iа V + М, то сопутствующий воспроизводству процесс обращения (об-

ВТОРАЯ КНИГА. ПРОЦЕСС ОБРАЩЕНИЯ КАПИТАЛА 287

мен между различными сферами) достиг бы тем самым своей цели.

Но вне сферы b₁, охватывающей все отрасли промышлен­ности, производящей прямые средства производства (това­ров I а), находятся другие сферы производства, которые про­изводят средства производства сферы b₁. Следовательно, V_b + + М_b должны иметь большую стоимость, чем V_b1 + M_bl; следовательно, так как стоимость товаров b₁, которые возме­щают С _α, больше, чем V_b1 + M_b1,то часть этих товаров b₁, обмениваемых на С_а, должна образовывать часть постоянной части стоимости продукта b_l; часть стоимости C_b1, которая снова должна быть возмещена за счет С_b2.

Эта часть С_b1, которая должна быть возмещена за счет C_b2, может быть равна только (V + М)_b2, — совершенно так же, как С_а был равен (V + М)_b. (Предполагается, что все отрасли промышленности, которые доставляют средства производства для С_b1, объединены в сфере b₂.)

Масса товаров b), равная (V + М)_b = С _α, продается им [классу] а). Но эта масса больше, чем (V + М)_b1, то есть больше, чем та часть стоимости продукта b₁, которая может быть израс­ходована на предметы потребления. Поскольку С_а > (V + M)_bl, постольку [классу] а) продается часть постоянной части стои­мости C_b1, которая снова возмещена в своей натуральной форме посредством обмена с b₂;таким образом, что перешедшие к b₁ в первую очередь предметы потребления а), или их стоимость (равная С_а) — поскольку эта стоимость больше (V + M)_b1, — в действительности переходят от b₁ к b₂, a b₂ доставляет вза­мен снова подлежащую возмещению часть С_b1. Часть стоимо­сти b₂, которая таким образом обменивается на часть C_bl, должна быть равна (V + M)_b2, так как b₂ должен обменять на предметы потребления только (V + M)_b2. Если бы обме­ниваемая таким образом на b₂ часть C_bl была больше (V + M)_b2, то она охватывала бы часть C_b2, который тогда нужно было бы снова обменивать на товар b₃ на сумму (V + М)_b3 и т. д., — до тех пор, пока расчет не удастся завершить без остатка. Поэтому для наглядности достаточно предположить, что кроме класса b¹ существует еще класс b₂, так что (V + M)_bl + + (V + M)_b2 = (V + M)_b, то есть равны сумме стоимости всех V + М, заключающихся в прямых и косвенных сред­ствах производства а).

288 К. Маркс

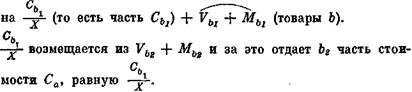
Следовательно, процесс таков: Са целиком обменивается

Следовательно, в действительности (V + M)_b1 + (V + Μ)_b2 возмещаются в натуральной форме за счет С _α, в то время как

(V + M)_b2.

Вследствие этого распределение части предметов потреб­ления, равной С_а, между (V_bl + M_bl) + (V_b2 + M_b2), то есть между (V + M)_b1 сопровождается возмещением всего постоян­ного капитала а) из b₁) и части постоянного капитала b¹) — из b₂.

III) Следовательно, после того как это движение завер­шено:

1) вся совокупность предметов потребления — весь про­дукт а) — распределена между рабочими и капиталистами классов а), b₂) и b₂). (V_a + М_а) присвоены их производителем а) in natura, и часть стоимости продукта а), равная С _а, рас­пределена так, что часть ее на сумму V_bl + M_b1 попала к клас­су b₁ а другая часть, на сумму V_b2 + M_b2, — к классу Ь₂. Весь доход общества распределен.

С другой стороны, в натуральной форме возмещены:

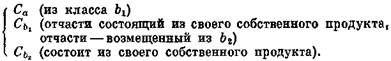
Единственное обращение, которое может еще совершиться,— это внутри класса b₁ (между различными сферами производ­ства, образующими этот класс) и внутри b₂; возможен также еще частичный обмен между C_b1 и С_b2.

Все это обращение, следовательно, совершается только между постоянным капиталом классов b₁ и b₂.

Между а), b₁) и b₂) обращение совершается лишь до тех пор, пока С_а не возмещен in natura и (V + Μ) (b₁ и b₂) не реа-

ВТОРАЯ КНИГА. ПРОЦЕСС ОБРАЩЕНИЯ КАПИТАЛА 289

лизованы в предметах потребления а). Поэтому это тот обмен — именно этот последний, — на явлениях которого основывается ложное представление А. Смита и т. д.

[197] I α) С_α(T) ⁵⁰ + С_αα(T) ³⁵⁰ + V_а ¹⁰⁰(деньги) + M_а(T) ¹⁰⁰

II αα) С_αα(T) ²⁵⁰+ С_α(T) ²⁰⁰ + V_αα ¹⁰⁰(деньги) + 50 ф. ст. деньгами

+ 50 ф. ст. в фонде потребления I α) С_α(T) ⁴⁰⁰ + V_α ¹⁰⁰ (деньги)

+ 50 ф. ст. для обращения прибавочной стоимости.

IIαα покупает на 50 ф. ст. T I a, I a покупает на 50 ф. ст. Т IIαα, и к IIαα окончательно притекают те 50 ф. ст. денег, которые он авансировал.

Мы имеем:

I a) C_a ⁴⁰⁰(в виде средств производства аа) + V_a ¹⁰⁰(в виде денег)

 

+ M_a(T) ¹⁰⁰

(Допустим, что на обращение М_а ¹⁰⁰в этом классе пред­назначаются 50 ф. ст.)

IIαα) C_αα(Т) ²⁰⁰ + С²⁰⁰ (в виде средств производства товаров а)

+ V_αα ¹⁰⁰(деньгами)

+ 50 ф. ст. деньгами для обращения прибавочной стои­мости.

IIα) C_α(Т) ¹⁰⁰ + V_a ¹⁰⁰ (деньгами)

+ 50 ф. ст. для обращения прибавочной стоимости.

В целом на обращение здесь авансированы: 300 ф. ст. — на выплату заработной платы V (а, αα, α и др.) и 150 ф. ст. — на обращение прибавочной стоимости (50 ф. ст. — в I а, 50 ф. ст.— в IIαα, 50 ф. ст. — в IIα).

Как и раньше, авансированных в IIαα и IIα на обращение V + M денег должно хватить для того, чтобы вновь превра­тить C_a ⁴⁰⁰из формы товара (предметов потребления) а)в форму средств их производства αα); далее, для обмена V _αα¹⁰⁰(как до­хода рабочих αα) на товар а); также для обратного притока денежной формы V _αα¹⁰⁰как денежной формы переменного капи­тала; также — для реализации М _ααв товаре I а и для об­ратного притока в IIαα денег, авансированных на реализацию прибавочной стоимости IIαα в пределах IIαα. Наконец, этих денег достаточно для того, чтобы превратить часть постоянного капитала IIαα, равного (V + М) IIα, в средства производства α, восстановить денежную форму переменного капитала IIα, обе­спечить обратный приток денег, авансированных на обраще­ние прибавочной стоимости в IIα, — точно так же,как и для