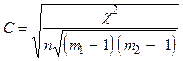,
де c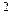 
= 
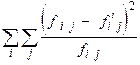– сума стандартизованих відхилень фактичних частот розподілу від теоретичних; m 1 та m 2 – кількість груп за першою і другою ознаками; n – кількість елементів сукупності.
Розрахунок c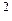 
подано в таблиці 7.13. Теоретичні частоти обчислюють на основі підсумкових частот 
.
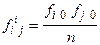Наприклад, 
і т. д.
Таблиця7.13. Розрахункова таблиця
| Група i j | f i j | f ‘ i j | f i j – f ‘ i j | (f i j – f ‘ i j) | (f i j – f ‘ i j) / f ‘ i j |
| 28,0 | |||||
| -6 | 3,3 | ||||
| -8 | 7,1 | ||||
| -7 | 4,4 | ||||
| 13,1 | |||||
| -5 | 8,0 | ||||
| -7 | 7,0 | ||||
| -7 | 4,1 | ||||
| 19,6 | |||||
| Разом | - | 96,3 |
Коефіцієнт співзалежності становить 0,49, тобто
.
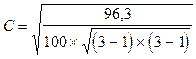Перевірку істотності зв’язку здійснюють за допомогою критерію c 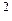з числом ступенів вільності K = (m 1 – 1) (m 2 – 1) = 2 x 2 = 4.
Критичне значення c 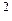(0,95) (4) = 9,49 значно менше від фактичного c 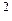= 96,3, отже, зв’язок між віком подружжя істотний.
Завдання 7.14
Необхідно:
– обчислити коефіцієнт рангової кореляції та перевірити істотність зв’язку між результатами лижників у кросах і лижних гонках з імовірністю 0,95.
Дані для виконання:
Підсумкові результати в кросах (ранг Х) і лижній гонці (ранг Y) у 10 лижників розподілились так:
| X | ||||||||||
| Y |
Розв’язок. Коефіцієнт рангової кореляції визначають за формулою Спірмена
r = 1 –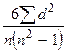 
,
де n – кількість елементів сукупності; d =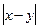 
– відхилення рангів.
Розрахунок суми квадратів відхилень рангів наведено в таблиці 7.14.
Таблиця7.14. Розрахунок суми квадратів відхилень рангів
| X | Y | d =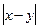
| d |
| - | - | - |
За розрахунком коефіцієнт рангової кореляції становить 0,83.
Критичне значення r для a = 0,05 наведено в додатку. Для n = 10 критичне значення r 0,95 = 0,563 менше від фактичного, що свідчить про істотний зв’язок між ознаками.
Завдання 8.1
Необхідно:
– дати повну і змістовну відповідь на наступні питання.
Дані для виконання:
1. Сутність вибіркового спостереження. та характеристика основних видів вибірок
2. Основні види вибірок
3. Види і порядок розрахунку помилок вибіркового спостереження
Завдання 8.2
Необхідно:
– обчислити середні витрати часу на завантаження вагона шихтою та з імовірністю 0,997 помилку вибірки для середньої.
Дані для виконання:
За даними вибіркового обстеження, витрати часу на завантаження вагону шихтою з вугільної башти становлять, с: 104, 113, 110, 108, 105, 97, 103, 111, 119, 100.
Завдання 8.3
Необхідно:
– за даними таблиці 8.1 обчислити: 1) середнє число дітей у сім’ях переселенців та довірчий інтервал для середньої з імовірністю 0,954; 2) з такою самою імовірністю граничну помилку та довірчий інтервал для частки сімей, які мають троє і більше дітей.
Дані для виконання:
Таблиця 8.1. Дані 20%-го вибіркового обстеження 100 сімей переселенців із зони жорсткого радіаційного контролю
| Число дітей | Разом | ||||||
| Число сімей |
Завдання 8.4
Необхідно:
– за даними таблиці 8.2 обчислити: 1) середній строк служби верстатів та довірчий інтервал для середньої з імовірністю 0,997; 2) граничну помилку і довірчий інтервал для частки верстатів, строк служби яких більш, як 12 років, з такою самою імовірністю.
Дані для виконання:
Таблиця 8.2. Дані 5%-го вибіркового обстеження верстатів за строком служби
| Строк служби, років | до 4 | 4 – 8 | 8 – 12 | 12 і більше | Разом |
| Кількість верстатів |
Завдання 8.5
Необхідно:
– за даними табл. 8.3 визначити середній процент під кредит, граничну помилку та довірчий інтервал для середньої з імовірністю 0,954.
Дані для виконання:
Комерційні банки надають кредит на купівлю автомобілів під 12%, дилери, що торгують автомобілями, – 8 – 16%.
Таблиця 8.3. Дані вибіркового обстеження 25 дилерів
| Процент під кредит | 8 – 10 | 10 – 12 | 12 – 14 | 14 і більше |
| Число дилерів |
Завдання 8.6
Необхідно:
– визначити: 1) з імовірністю 0,954 граничну помилку та довірчий інтервал для частки тих відповідей, що передбачають поліпшення ситуації, припускаючи, що думку висловили випадково відібрані бізнесмени; 2) яка має бути вибіркова сукупність, щоб точність висновку щодо погіршення ситуації на ринку з імовірністю 0,997 не перевищила 5%.
Дані для виконання:
При опитуванні, яке проводилось асоціацією промисловців відносно перспектив торгівлі в найближчі півроку, думки 64 бізнесменів розподілилися так: 28 осіб вважають, що ситуація поліпшиться, 16 – погіршає, 20 осіб – змін не передбачається.
Завдання 8.7
Необхідно:
– встановити, яка має бути вибіркова сукупність, щоб помилка вибірки для частки працюючого без простоїв обладнання з імовірністю 0,954 не перевищила 5%.
Дані для виконання:
За даними пробного вибіркового обстеження роботи ковальсько-пресового обладнання (обсяг вибірки – 16), в першу зміну без простоїв працювало 80% машин.
Завдання 8.8
Необхідно:
– за даними таблиці 8.4 визначити: 1) середній вміст жиру в молоці; 2) середнє квадратичне відхилення і дисперсію вмісту жиру; 3) з імовірністю 0,954 граничну помилку вибірки та інтервал, в якому знаходиться середній вміст жиру в молоці.
Дані для виконання:
Таблиця 8.4. Вміст жиру у 15 партіях молока
| Вміст жиру, % | Кількість партій |
| 2,8 | |
| 2,9 | |
| 3,0 | |
| 3,4 |
Завдання 8.9
Необхідно:
– за даними таблиці 8.5 визначити: 1) середній відсоток вологості; 2) середнє квадратичне відхилення; 3) з імовірністю 0,997 граничну помилку вибірки для середньої вологості всієї партії виробів.
Дані для виконання:
Таблиця 8.5. Дані вибіркового обстеження трьох відсотків виробів партій готової продукції
| Відсоток вологості | До 15, 0 | 15,0 – 17,0 | 17,0 – 19,0 | 19,0 – 21,0 | 21,1 – 23,0 |
| Кількість виробів |
Завдання 8.10
Необхідно:
– за даними табл. 8.5 визначити з ймовірністю 0,997, в яких границях коливається середній відсоток природного убутку в генеральній сукупності.
Дані для виконання:
Таблиця 8.5. Дані обстеження 100 рівних за вагою партій
| Відсоток природного убутку | 3 – 5 | 5 – 7 | 7 – 9 | 9 – 11 | 11 – 13 | Разом |
| Кількість партій товару |
Завдання 8.11
Необхідно:
– за даними табл. 8.6 визначити середнє навантаження на одного продавця, середнє квадратичне відхилення; з ймовірністю 0,954, в яких границях міститься середній розмір навантаження в генеральній сукупності.
Дані для виконання:
Таблиця 8.6. Дані обстеження 100 продавців
| Товарообіг на одного продавця, млн. грош. од. | 1 – 5 | 5 – 10 | 10 – 15 | 15 – 20 | Разом |
| Кількість продавців |
Завдання 8.12
Необхідно:
– за даними табл. 8.7 визначити ймовірність того, що помилка репрезентативності при визначенні середньої зольності вугілля не перевищує 0,3 %.
Дані для виконання:
Із різних вагонів вугілля, який надійшов на електростанцію, в порядку випадкової і безповторної вибірки взято 100 проб для визначення зольності. На підставі аналізу отримані наступні дані:
Таблиця 8.7. Дані вибіркового обстеження 100 проб за рівнем зольності
| Зольність, % | До 12 | 12 – 14 | 14 – 16 | 16 – 18 | 18 – 20 | Більше 20 |
| Число проб |
Завдання 8.13
Необхідно:
– за даними таблиці 8.8 з ймовірністю 0,954 визначити границі, в яких можна очікувати середні витрати часу на виготовлення одної деталі всіма верстатними підприємствами. З ймовірністю 0,997 визначити частку верстатників, у яких витрати часу вище 25 хвил.
Дані для виконання:
Для вивчення продуктивності праці верстатників заводу проведено 10 %-ве вибіркове обстеження за методом безповторного відбору.
Таблиця 8.8. Дані вибіркового обстеження робітників-верстатників для визначення продуктивності праці
| Час обробки деталі, хвил. | 17 – 19 | 17 – 21 | 21 – 23 | 23 – 25 | 25 – 27 |
| Число працівників |
Розв’язок типових завдань
Завдання 8.14
Необхідно:
– за даними таблиці 8.8 визначити: 1) середню міцність ниток та граничну помилку вибірки для середньої з імовірністю 0,954; 2) частку ниток, міцність яких більша за 90 г, та граничну помилку для частки з імовірністю 0,954.
Дані для виконання:
дало такі результати.
Таблиця 8.8. Дані вибіркове випадкового обстеження 20 проб пряжі на міцність
| Міцність ниток, г | до 50 | 50 – 70 | 70 – 90 | 90 і більше | Разом |
| Число проб |
Розв’язок. 1. Граничну помилку вибірки для середньої обчислюють за формулою
D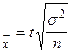 
,
де n – обсяг вибіркової сукупності;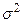 
– дисперсія ознаки x; t – коефіцієнт довіри (для імовірності 0,954 цей коефіцієнт становить 2).
Розрахунок середньої міцності ниток і дисперсії цього показника показано в таблиці 8.9.
Таблиця8.9. Розрахунок середньої міцності ниток і дисперсії
| Значення варіанта х (середина інтервалу) | Частота f | xf | _ x – x | _ 2 (x – x) f |
| -20 | ||||
| +20 | ||||
| +40 | ||||
| Разом | - |
За розрахунками,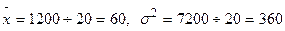 
. Помилка вибірки середньої з імовірністю 0,954 становить
D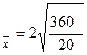 
= 8,5 г.
2. Частка ниток, міцність яких більша за 90 г, становить 10% (р = 2: 20 = 0,1), а дисперсія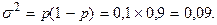 
Гранична помилка вибірки для частки з імовірністю 0,954 дорівнює 13,4%, тобто D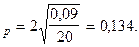 
Завдання 8.15
Необхідно:
– обчислити: 1) середні втрати зерна в розрахунку на одну пробну ділянку та довірчі межі середніх втрат для всієї площі озимої пшениці з імовірністю 0,954; 2) мінімально достатній обсяг вибірки, при якому помилка з імовірністю 0,954 не перевищить 1 ц/га
Дані для виконання:
Проведено вибіркове обстеження втрат зерна озимої пшениці в зв’язку з несвоєчасним збиранням врожаю. Число пробних ділянок визначалось пропорційно площі посіву відповідного сорту пшениці (розшарована вибірка). Результати обстеження занесено в таблицю 8.10.
Таблиця 8.10. Дані вибіркового обстеження втрат зерна озимої пшениці в зв’язку з несвоєчасним збиранням врожаю
| Сорт пшениці | Кількість пробних ділянок | Втрати зерна, ц/га | Дисперсія втрат зерна |
| Одеська – 2 | 6,4 | ||
| Народна – 4 | 7,8 | ||
| Черкаська – 3 | 10,3 |
Розв’язок. 1. Середні втрати зерна обчислюють за формулою середньої арифметичної зваженої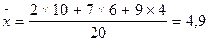 
ц / га.
Довірчі межі середньої визначають згідно з теорією вибіркового методу
.
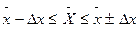При обчислені граничної помилки D x розшарованої вибірки використовують середню з групових дисперсій. В нашому прикладі
,
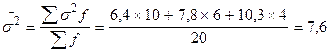а гранична помилка – D x =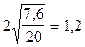 
ц/га.
Отже, середні втрати зерна від несвоєчасного збирання урожаю на всій площі посіву озимої пшениці становлять 4,9 ± 1,2, тобто не менш як 3,7 і не більш як 6,1 ц/га.
2. Розрахунок мінімально достатньої вибіркової сукупності здійснюють за формулою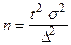 
.
Умовою задачі передбачено D х = 1 ц/га. Таку точність результатів забезпечує обстеження 30 пробних ділянок: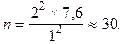 
Завдання 9.1
Необхідно:
– дати повну і змістовну відповідь на наступні питання.
Дані для виконання:
1. Види й основні характеристики рядів динаміки
2. Вирівнювання динамічних рядів
3. Виявлення та вимірювання сезонних коливань
4. Аналіз рядів динаміки і прогнозування рівнів ряду
Завдання 9.2
Необхідно:
– за даними таблиці 9.1 обчислити базисні і ланцюгові характеристики динаміки: абсолютні прирости, темпи зростання і темпи приросту.
Дані для виконання:
Таблиця 9.1 Динаміка витрат на збут ВАТ “Дніпро”
| Роки | |||||||
| Витрати на збут, млн. грн. | 2000,0 | 2344,0 | 1997,0 | 2450,0 | 3430,0 | 3540,0 | 5567,0 |
Завдання 9.3
Необхідно:
– за даними таблиці 9.2 обчислити базисні характеристики динаміки: абсолютні прирости і темпи приросту.
Дані для виконання:
Таблиця 9.2. Динаміка собівартості ВАТ “Нортон”
| Роки | |||||||
| Собівартість товарів, млн. грн. | 17855,0 | 66778,0 | 55734,0 | 66790,0 | 266750,0 | 99543,0 | 46678,0 |
Завдання 9.4
Необхідно:
– за даними таблиці 9.3 обчислити ланцюгові характеристики динаміки: абсолютні прирости і темпи приросту, абсолютні значення 1% приросту. Показати взаємозв’язок названих характеристик
Дані для виконання:
Таблиця 9.3. Динаміка виробництва будівельної цегли в регіоні характеризується такими даними, млн. шт.
| Рік | ||||||||
| Кількість, млн. шт. |
Завдання 9.5
Необхідно:
– за даними таблиці 9.4, використовуючи взаємозв’язок характеристик динаміки, визначити обсяги виробництва пральних машин, абсолютну та відносну швидкість його зростання.
Дані для виконання:
Таблиця9.4. Ланцюгові характеристики динаміки виробництва
пральних машин
| Рік | Виробництво пральних машин, тис. шт. | Ланцюгові характеристики динаміки | |||
| абсолютний приріст, тис. шт. | темп зростання, % | темп приросту, % | абсолютне значення 1% приросту, тис. шт. | ||
| – | – | – | – | ||
| ? | ? | ? | ? | ? | |
| ? | ? | ? | 3,9 | ||
| ? | ? | ? | 6,6 | ? | |
| ? | ? | 102,1 | ? | ? | |
| ? | ? | ? | ? |
Завдання 9.6
Необхідно:
– за даними таблиці 9.4 визначити вид ряду динаміки, середньорічні темпи росту (зменшення), побудуйте прогноз на 2005 рік та відобразіть його графіком.
Дані для виконання:
Таблиця 9.4. Випуск продукції промисловості області характеризується такими даними за 1998-2004 рр.
| Роки | |||||||
| Випуск продукції промисловості, млн. грн. | 3440,0 | 4435,0 | 5554,0 | 3456,0 | 5561,0 | 3345,0 | 8133,0 |
Завдання 9.7
Необхідно:
– за даними таблиці 9.5 визначити прогностичні рівні обсягу виробництва на 2005 рік та середньорічні темпи їх зниження (зростання).
Дані для виконання:
Таблиця9.5. Виробництво основних видів продовольчих товарів на душу населення області характеризується такими даними за 2000 – 2004 рр.
| Продукти, кг | Роки | ||||
| М’ясо | 53,2 | 47,8 | 39,3 | 28,4 | 24,3 |
| Молоко | 123,9 | 108,8 | 78,8 | 53,7 | 50,1 |
| Цукор-пісок | 130,9 | 92,0 | 69,9 | 76,5 | 70,2 |
| Олія | 20,6 | 19,3 | 16,4 | 15,4 | 15,2 |
| Хлібопродукти | 129,0 | 128,6 | 123,5 | 104,3 | 111,2 |
Завдання 9.8
Необхідно:
– за даними таблиці 9.6 розрахувати абсолютний приріст, темп зростання, темп приросту базисним і ланцюговим способами, середньорічний темп зростання власного капіталу.
Дані для виконання:
Таблиця 9.6. Динаміка власного капіталу підприємств Житомирської області
| Роки | |||||||
| Власний капітал, млн. грн. | 2000,0 | 2344,0 | 1997,0 | 2450,0 | 3430,0 | 3540,0 | 5567,0 |
Розв’язок типових завдань
Завдання 9.9
Необхідно:
– за даними таблиці 9.7 визначити: 1) базові і ланцюгові характеристики динаміки: абсолютні прирости, темпи зростання і приросту, абсолютні значення 1% приросту; 2) середньорічні темпи зростання і абсолютні прирости за 1985 – 1990 та 1991 – 1995 рр.
Дані для виконання:
Таблиця 9.7. Динаміка виробництва промислових роботів в об’єднанні
| Рік | |||
| Кількість, шт. |
Розв’язок. Абсолютний приріст Dt показує, на скільки одиниць власного виміру рівень ряду yt більший (+) чи менший (–) за рівень, взятий за базу порівняння (yt- 1 чи y 0):
ланцюговий Dt= yt – yt- 1,
базовий D t = yt – y 0.
Так, за 1985 – 1990 рр. виробництво промислових роботів зросло на 54 шт. (114 – 60), за 1990 – 1995 рр. – на 12 шт. (126 – 114). За весь період абсолютний приріст становив 66 шт. (126 – 60).
Темп зростання показує, в скільки разів один рівень ряду більший за інший:
ланцюговий tt =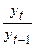 
,
базовий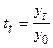 
.
За 1985 – 1990 рр. виробництво роботів збільшилось в 1,9 рази (114: 60), за 1990 – 1995 рр. – в 1,1 рази (126: 114). Базовий темп зростання за весь період становив 2,1 рази (126: 60).
Темп приросту показує, на скільки процентів значення yt більше (+) чи менше (–) за рівень, який прийнятий за 100%: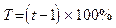 
У нашому прикладі темпи приросту становлять: ланцюгові 190 – 100 = 90%, 110 – 100 = 10%; базовий – 210 – 100 = 110%.
Абсолютне значення 1% приросту можна обчислити як частку відділення абсолютного приросту на темп приросту: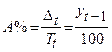 
; 54: 90 = 0,60; 66: 110 = 0,60, тобто вага відносно приросту є не що інше, як сота частина рівня, взятого за базу порівняння.
Середньорічний абсолютний приріст – це середнє з ланцюгових абсолютних приростів: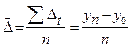 
, де уп – кінцевий рівень ряду. За 1985 – 1990 роки 
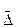= 54: 5 = 10,8; за 1990 – 1995 роки 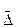= 12: 5 = 2,4.
Середньорічний темп зростання визначають за формулою середньої геометричної
.
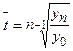У нашому прикладі за 1985 – 1990 рр.
;
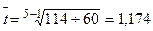за 1990 – 1995 рр.
.
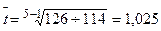Середньорічний приріст виробництва промислових роботів за 1985 – 1990 роки становив 17,4%, за 1990 – 1995 роки – 2,5%.
Прискорення (сповільнення) зростання обчислюють зіставленням однойменних характеристик швидкості зростання. Наприклад, абсолютних приростів: d t = D i – D i -1 = 2,4 – 10,8 = –8,4.
Значення d t < 0 свідчить про сповільнення зростання. Темп сповільнення абсолютної швидкості обчислюють відношенням абсолютних приростів
g t = 2,4: 10,8 = 0,222.
Прискорення (сповільнення) відносної швидкості є частка від ділення середньорічних темпів зростання. Дільником виступає більший за значенням. У нашому прикладі g t = 1,137: 1,024 = 1,111.
Завдання 10.1
Необхідно:
– дати повну і змістовну відповідь на наступні питання.
Дані для виконання:
1. Сутність, призначення та види індексів
2. Загальні агрегатні індекси кількісних та якісних показників
3.Аналіз співвідношень середніх рівнів
4. Ланцюгові та базисні індекси
