Кути многокутника. Прямий кут. Прямокутник.
Периметр многокутника
Зміст роботи розкриємо окремо для кожного класу.
У 1 класі учні ознайомлюються з трикутником, чотирикутником, п'ятикутником і шестикутником. Діти повинні засвоїти правильні назви цих многокутників, вміти їх розпізнавати. З цією метою многокутники, а також круг постійно використовуються як дидактичний матеріал. За програмою розгляд елементів многокутника у 1 класі не передбачено, але багато вчителів у ході аналізу того чи іншого многокутника пропонують показати і полічити сторони, вершини, кути. Таке випередження допустиме, але не слід його вводити в ранг програмових вимог.
У процесі вивчення нумерації чисел першого десятка практикується складання многокутників з паличок, вирізування з паперу, а також розпізнавання многокутників на предметах оточення та малюнках.
Новою вправою буде в цей час розгляд многокутника, поділеного відрізком на дві фігури, і визначення назви кожної фігури (мал. 163).

Мал. 163
Робота з формування уявлень учнів про круг і многокутники проводиться в тісному зв'язку з уроками праці й образотворчого мистецтва. Діти складають фігури з паперу, малюють їх, використовують фігури для різноманітних аплікаційних робіт, малюють орнаменти з геометричними фігурами.
У 2 класі продовжується робота з формування уявлень учнів про многокутники і круг. Пропонуються дещо ускладнені вправи на розпізнавання многокутників, на поділ фігур на многокутники і немногокутники. Учні вивчають елементи многокутників, вимірюють довжини їх сторін.
Поняття кута і вершини трикутника (многокутника) вводять (конкретизують) за допомогою запитань: Скільки в трикутнику кутів? Вершин? Сторін?
Сторони, вершини і кути многокутника потрібно показувати учням на моделях плоских фігур. Кут бажано показати віялоподібним рухом указки, один кінець якої суміщений з вершиною кута многокутника. Треба звернути увагу дітей на те, що вершина многокутника є і вершиною відповідного кута. Бажано показати їм, що кути є різні за величиною, але величина кута не залежить від довжини його сторін.
Прямий кут. Для ознайомлення з прямим кутом варто розглянути його утворення в процесі перегинання листка паперу. Кожному учневі треба дати аркуш паперу довільної форми. Потім під керівництвом учителя діти складають аркуші вдвічі, притискують лінію згину. Після цього аркуш перегинають ще раз, стежачи за тим, щоб частини утвореної раніше лінії перегину сумістилися. Утвориться кут. Такий кут називається прямим. Якщо папір розгорнути, діти побачать, що дві лінії перегину поділяють аркуш на чотири частини. Утворилось чотири прямі кути, які мають спільну вершину.
За допомогою паперової моделі прямого кута учні відшукують прямі і непрямі кути на предметах з навколишнього оточення і на косинці. Після цього користуються прямим кутом косинця.
Прямокутник. Дітям пропонують розглянути малюнки чотирикутників і знайти серед них такі, в яких всі кути прямі (мал. 164). Після цього подають означення прямокутника.
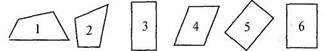
Мал. 164
Варто звернути увагу учнів на форму навколишніх предметів або їх частин. Вони знаходять предмети, що мають форму прямокутника: зошит, книжка, кришка стола, класна дошка тощо.
У процесі вимірювання сторін прямокутника діти встановлюють, що його протилежні сторони рівні.
Через кілька уроків вводять поняття довжини і ширини прямокутника.
Квадрат. Квадрат вводять як рівносторонній прямокутник. Учитель пропонує серед даних на малюнку прямокутників або серед даних моделей знайти такі, в яких сторони рівні (мал. 165). Після цього він подає означення квадрата.

Мал. 165

Із введенням понять прямокутника і квадрата збагачуються вправи на розпізнавання многокутників. Адже тепер квадрат має чотири назви: квадрат, прямокутник, чотирикутник і многокутник, а прямокутник — три назви: прямокутник, чотирикутник і многокутник.
Наприкінці навчання в 2 класі запроваджуються вправи на розпізнавання многокутників у конфігураціях фігур.
Коло і круг. При введенні поняття кола і круга можна йти двома шляхами: а) розглянути спочатку коло як особливий вид кривої лінії, а потім ввести поняття круга як фігури, яку обмежує коло; б) розглянути круг, виходячи з відомого дітям поняття "кружечок", а коло ввести як лінію, яка обмежує круг. У зв'язку з тим, що кружечки, вирізані з паперу, потрібні для проведення предметної лічби вже з перших уроків математики, перевагу варто надати другому шляху.
Учитель повідомляє дітям, що на малюнку зображено круг (мал. 166).

Мал. 166
Лінія, яка є межею круга, називається колом. Коло будують за допомогою циркуля. Точка О, в якій міститься голка циркуля,— центр кола. Відрізок ОА — радіус кола.
З метою уточнення уявлень про коло і круг доцільно розглянути вправи виду:
.С

Мал. 167
Назвіть точки, які: а) належать кругу; б) належать колу; в) не належать у; г) належать кругу, але не належать колу (мал. 167).
Навчаючи дітей креслити коло за допомогою циркуля, вчитель спочатку демонструє таку побудову на аркуші білого паперу, прикріпленому до дошки. При цьому він ознайомлює їх з інструкцією побудови кола за допомогою циркуля:
1. Розвести ніжку циркуля і вістря олівця на величину заданого радіуса. Для цього голку треба встановити на нульову поділку лінійки, а вістря олівця — на поділку, числове значення якої дорівнює заданій величині радіуса.
2. Встановити голку в задану точку. Для цього правою рукою потрібно тримати олівець, а пальцем лівої руки спрямовувати вістря голки в задану точку.
3. Коло креслять в напрямі за годинниковою стрілкою, нахиливши циркуль трохи вперед у напрямі руху олівця. Починати креслити слід від нижньої точки кола (від себе).
4. Креслити коло треба однією правою рукою, тримаючи олівець за верхній кінець.
5. Лікоть правої руки спочатку відведений від корпуса, а відповідно до наближення вістря олівця до кінця (і початку) кола поступово наближається до нього.
Спочатку учні вчаться будувати коло на окремих аркушах паперу (на чернетках). Коли вони більш-менш правильно навчаться креслити коло, можна дозволити побудову кола в зошиті.
Є сенс і в тому, щоб ввести у 2 класі поняття діаметра кола. Вчитель пропонує дітям провести відрізок, який би проходив через центр кола і сполучав дві точки кола. Потім він повідомляє, що такий відрізок називається діаметром кола. Діаметр кола складається з двох радіусів.
Він поділяє круг на дві рівні частини.
Периметр многокутника. Означення периметра многокутника вводять у 2 класі. Як і довжину ламаної лінії, периметри многокутників знаходять у результаті вимірювання довжин їх сторін з подальшим додаванням здобутих результатів.
У 3 класі вводять буквене позначення многокутників. Це дає змогу урізноманітнити постановку завдань з геометричним змістом. Наприклад, серед даних фігур назвати прямокутники, квадрати тощо.
Пропонуються різні вправи на побудову многокутників на папері в клітинку. Причому такі завдання ускладнюють поділом фігури на задані многокутники.
Учні продовжують виконувати вправи на знаходження периметра многокутника. При цьому їм потрібно показати різні способи обчислення. Якщо довжину прямокутника позначити буквою а, а ширину — буквою Ь, то ці способи можна записати так: а + Ь + а + Ь; а + а + Ь + Ь; а • 2 + Ь • 2; (а + Ь) • 2. Останній спосіб найзручніший, але учні повинні бути ознайомлені з усіма способами.
У 4 класі діти продовжують виконувати вправи на розпізнавання і побудову плоских фігур, розв'язують інші задачі з геометричним змістом.
Геометричні задачі, пов'язані з периметром, дещо ускладнюються, більшість з них пов'язана з поняттям площі фігури.
Спостереження геометричних тіл і введення їх назв. Перші уявлення про геометричні тіла діти отримують у дошкільному віці. У початкових класах для розвитку цих уявлень можна використати уроки математики, малювання, а також моделювання з пластиліну на уроках праці, прогулянки та екскурсії.
Можливі такі види роботи з геометричними тілами: розгляд предметів, моделей, малюнків, що мають певну геометричну форму; поступове введення назв геометричних тіл; знаходження в навколишньому середовищі предметів відповідної назви (форми); моделювання геометричного тіла з пластиліну; виділення деяких елементів тіла (вершини, ребра, грані, основи); малювання на папері за зразком і вказівками вчителя.
У початкових класах варто дати школярам також поняття про такі геометричні тіла: кулю, куб, циліндр, прямокутний паралелепіпед, конус та піраміду.
Рівняння.
Поняття рівняння тісно пов’язане з поняттям виразу, змінної, рівності.
З рівняннями діти ознайомлюються у 3 класі. Відповідна підготовча робота розпочинається з 1 класу. Вона передбачає виконання вправ з “віконцями” та знаходження невідомого компонента арифметичних дій на основі зв’язків між компонентами та результатами арифметичних дій.
Розв’язування рівнянь. Ознайомлення з рівняннями ґрунтується на двох вправах, поданих нижче.
Вправа І. Порівняй і замість зірочки постав знак “>”, “<“ або “=”, якщо відомо, що в усіх випадках х = 5.
х+ 22 * 25 х~ 2 * 10
х + 5 * 10 х— 1*4
Після перевірки правильності виконання завдання вчитель пропонує учням виписати в окремий рядок усі рівності і повідомляє їм, що рівності зі змінною (з невідомим) називають рівняннями. У кожному з виписаних рівнянь невідоме дорівнює 5. Це розв’язок кожного з даних рівнянь.
Вправа 2
13 ~х = 8 х + 5 = 10 х~ 1 = 4
Це — рівняння. Розв’язати рівняння означає знайти те числове значення букви, при якому рівність буде правильною.
Перевірте (усно), чи правильно розв’язані рівняння, х + 8 = 11 20 + х = 52
х = 11 - 8 л: = 52 — 20
х = 3 х = 32
Після виконання завдання вчитель повідомляє, що невідомий доданок у рівнянні можна знаходити добором або за правилом знаходження невідомого доданка.
На наступному уроці вчитель подає зразок міркування при розв’язуванні рівняння на знаходження невідомого доданка.
Міркування. У рівнянні х + 7 = 70 невідомий перший доданок, відомі другий доданок і сума. Щоб знайти невідомий доданок, треба від суми відняти відомий доданок. Запишемо рівняння так: х + 7 = 70 х= 70 — 7 = 63 Перевіримо (усно):
63 + 7 = 70
70 = 70
Рівняння на знаходження зменшуваного або від’ємника пропонують учням після повторення правил на знаходження відповідних компонентів.
У 3 класі діти вчаться розв’язувати рівняння на знаходження невідомого множника, діленого, дільника. Кожне з цих рівнянь розглядають одразу після ознайомлення з відповідним правилом. До розгляду правил учні мають справу
3 рівняннями цього виду на рівні вправ з “віконцями”. У процесі формування вмінь розв’язувати рівняння практикують як усне розв’язування, так і з записами у зошиті.
З усіма різновидами рівнянь на знаходження невідомого компонента учні ознайомлюються в 3 класі. У 4 класі вони лише закріплюють навички, розв’язують рівняння в нових числових межах. Однак вважаємо, що учнів
класу потрібно ознайомити з розв’язуванням рівнянь на дві операції.
23. Числові рівності і нерівності
Тотожне перетворення числового виразу — це заміна одного виразу іншим без зміни його значення. В процесі обчислень складених виразів ми постійно виконуємо тотожні перетворення.
Процес перетворення виразів, крім безпосередніх обчислень, відбувається під час виконання ряду вправ. Найбільш типовими серед них є такі: заміна числа сумою двох доданків (7 = 2 + 5); заміна числа розрядними доданками (235 = 200 + ЗО + 5); перетворення виразу на основі означення дії множення (4 + 4 + 4 = 4 • 3); обчислення у вигляді ланцюжка рівностей (7 + 8 = 7 і + (3 + 5) = 10 + 5 = 15); ілюстрування правил чи властивостей арифметичнії і дій ((20 —3) • 4 = 20 • 4 - 3 • 4).
Одним з видів роботи з перетворення виразів є їх порівняння. У початкомич класах його проводять здебільшого на основі порівняння значень виразін
У деяких вправах порівняння виконують на основі властивос'П'11 арифметичних дій. Саме в цих випадках більше виявляється “тотожнісп. виразів”. Наприклад: 4 • 3 + 4 • 6 = 4 • (3 + 6).
Порівняння виразів з використанням знаків “більше”, “менше" і “дорівнює” допомагає у розвитку самоконтролю під час проведенпч обчислень, стає основою у формуванні уявлень про числові, рівності І нерівності, про нерівності зі змінною.
У діючих підручниках вправ на порівняння достатньо, практикуються різні форми подання завдань (наприклад, порівняйте значення виразів і поставте потрібний знак; запишіть приклади, в яких відповідь менша за 50; випишіть вирази, між якими треба поставити знак та ін.).
Порівняння виразів і поняття про рівність використовуються під час ознайомлення з деякими властивостями арифметичних дій. Наприклад, порівнюючи вирази виду 7 + 3 і 3 + 7, учні знаходять, що значення виразів однакові. Отже, можна записати, що 7 + 3 = 3 + 7, і зробити висновок про переставну властивість додавання.
Потрібно стимулювати дітей до порівняння виразів на основі міркування. Наприклад: 9*9 — 3. Зліва — число 9, справа — від числа 9 відняли 3. Отже, справа стало менше, ніж 9. Тому 9 > 9 - 3.
9 + 3 * 10 + 5. У сумах зліва і справа перший доданок — 10.
Другий доданок зліва — 3, а справа — 5. Зліва додали менше, ніж справа. Отже, 10 + 3 < 10 + 5.
5 + 5 + 5 + 5*5-3. Зліва число 5 береться доданком 4 рази, а справа — тільки 3 рази. Отже, значення виразу зліва більше, ніж значення виразу справа, тому 5 + 5 + 5 + 5>5-3.
Корисні і подобаються учням вправи на порівняння виразів способом зміни порядку виконання арифметичних дій за допомогою дужок (наприклад, розставити дужки так, щоб рівності були правильними: 31 - 10 - 3 = 24; 4 • 7 - 4: 2 = 20).
24. Довжина. На першому етапі слід з’ясувати практичне значення ви мірювання, сам його процес. Учні отримують уявлення про сантимеі|і і вимірюють довжину відрізка за допомогою моделей сантиметра.
Потім діти ознайомлюються з лінійкою (покажіть початок лінійки, початок її відліку, перший, другий і т. д. сантиметр). Вони навчаються виконувані окремі операції: розміщувати аркуш паперу так, щоб руки і лінійка не закривали відрізка, який вимірюють; суміщати початок відліку лінійки і початком вимірюваного відрізка; розміщувати чотири пальці лівої руки так, щоб вони притискували середину лінійки до аркуша паперу.
Ознайомлення з дециметром та вимірювання довжини предметів і відрізків у дециметрах і сантиметрах проводяться під час вивчення чисел другого десятка. Учитель креслить на дошці відрізок завдовжки 50 см і пояснює, що вимірювати його довжину сантиметром незручно. Тому треба мати більшу одиницю вимірювання довжини. Потім показує смужку завдовжки 1 дм. Учні, маючи такі самі смужки, прикладають їх до шкали лінійки і встанов люють, що 1 дм = 10 см.
Первинне закріплення проводять за завданнями підручника. Учні розглядають моделі 1 см і 1 дм, визначають довжини відрізків, які поділено на сантиметри.
Ознайомлення з метром (у процесі вивчення нумерації чисел 21 — 100) проводять за таким планом: бесіда вчителя, за допомогою якої він підводить учнів до висновку, що великі відстані краще вимірювати більшими одиницями мір; показ демонстраційного метра для безпосереднього зорового сприймання; повідомлення співвідношень: 1 м = 100 см, 1 м = 10 дм; розгляд моделей метра, виготовлених з різних матеріалів; самостійне виготовлення дітьми метра з паперових смужок; вправи на вимірювання.
Вправи на вимірювання бувають подвійного роду: вимірювання відстані між двома пунктами (точками), наприклад, довжини та висоти класу, довжини шнурка та ін.; відмірювання відстаней, що дорівнюють даному числу метрів (наприклад, відміряти 3 м ниток).
У 3 класі вводяться нові одиниці вимірювання довжини (міліметр, кілометр), буквене позначення відрізків. Відрізки широко використовують пня розгляду понять збільшення і зменшення числа в кілька разів, кратного порівняння чисел та ін.
У 4 класі передбачається узагальнення набутих раніше знань, умінь і павичок вимірювання довжини. Учні під керівництвом вчителя складають іаблицю одиниць вимірювання довжини (табл. 32).
Таблиця 32
| м = | 10 дм | 1 км = | 1 000 м | |
| м = | 100 см | 1 дм = | 10 см | |
| м = | 1 000 мм | 1 см = | 10 мм |
Під час виконання практичних завдань, розв’язування задач, обчислення ішразів часто доводиться перетворювати складене іменоване число на просте і, навпаки, просте число на складене. Подамо зразки міркувань.
1. Подайте 3 790 см у метрах і сантиметрах. Один метр — це сто сантиметрів, тобто одна сотня сантиметрів. У числі 3 790 см стільки метрів, скільки в ньому всього сотень. У числі 3 790 всього 37 сотень. Отже, 3 790 см — цс 37 м 90 см.
2. Подайте 26 км 370 м у метрах.
Один кілометр — це одна тисяча метрів. 26 км — це 26 тисяч метрів та ще 370, буде 26 370 м.
25. Площа. З поняттям площі діти мають справу постійно. Вже дошкільники порівнюють предмети за площею (не називаючи самого слова “площа”). Ііони порівнюють не накладанням, а на око (наприклад, листок дуба більший, ніж листок берези). У початкових класах уявлення про площу стають чіткішими: фігури можуть бути різними й однаковими за площею.
У 4 класі учні ознайомлюються з поняттям площі. Вчитель повідомляє про те, що в розмовах, передачах по радіо, телебаченню часто можна почути: посівна площа, житлова площа, площа квартири, площа класної кімнати; що серед предметів, котрі нас оточують, багато таких, поверхня яких має форму трикутника, прямокутника, круга (дно каструлі — круг; підлога, стіни кімнати, класна дошка — прямокутники), кожна з них має площу. Порівнюючи площі фігур, виставлених на набірному полотні (наприклад, круг, трикутник, квадрат), діти встановлюють, що квадрат займає більше місце, ніж круг або трикутник. Учитель констатує, що в такому разі калVI* що площа квадрата більша, ніж площа кожної іншої фігури. Він зазначці що площа — це величина, яку можна не тільки порівнювати, а й вимірній Учні порівнюють площі фігур (мал. 113): найбільшу площу має прямокутно, площа квадрата більша, ніж площа круга або трикутника; проте порішиш» площі трикутника і круга важче. Після цього вчитель ставить завдання о мі годні на уроці ми будемо вчитися вимірювати площу).
Мал. 113
Далі він демонструє квадрат зі стороною 4 см і прямокутник зі сторонами З см і 5 см, пропонує порівняти площі цих фігур. Після одержання відпонІліЦ учитель повертає фігури, які на зворотному боці поділені на квадрат Підрахувавши ці квадрати, учні дізнаються, що площа квадрата більшії ні площу прямокутника.
Ознайомивши учнів з квадратним сантиметром, учитель проводи и. практичну роботу, пов’язану зі знаходженням площі фігур способом розбп 11 н її на квадратні сантиметри. Після цього знаходять площі прямокутнім їм (мал. 114, де лінійні розміри зменшено)
Мал. 114
Виміряйте довжину і ширину першого прямокутника. Яка його довжина і ширина? (8 см і 1 см). Як знайти площу прямокутника? (Розбити на квадраті сантиметри). Скільки їх? (8). У цьому прямокутнику вміщується стільці квадратних сантиметрів, скільки лінійних сантиметрів міститься в довжині Скільки квадратних сантиметрів у другому прямокутнику? (16). Як іш дізналися? (В одному ряду 8 см2, а таких рядів 2). Як по-іншому мо ї ми полічити квадрати? (В одному стовпчику 2 см2, а таких стовпчиків 8).
Знайдіть площу третього прямокутника. Не розбивайте весь прямокутно на квадрати. Покажіть тільки ряди, один з них розбийте на квадраті сантиметри. Яка площа прямокутника? (24 см2). Як ви про це дізнались? Як по-іншому можна знайти площу прямокутника? Чи потрібно розбивати прямі > кутник на ряди і квадрати? Чи можна відразу знайти площу прямокутники 1 Що для цього потрібно знати? (Довжину і ширину прямокутника).
Окремий урок відводиться для ознайомлення учнів з новими одиницями вимірювання площі. Вводяться відразу всі одиниці вимірювання плоіііі передбачені програмою. Основу бесіди складає таке повідомлення: “Площа одна з математичних величин. Для її вимірювання користуються не тільки
мівдратними сантиметрами, а й іншими одиницями. В табл. 33 подано одиниці намірювання площі, які найчастіше застосовуються в практичній діяльності”.
У процесі подальшого вимірювання й обчислення площі прямокутника і розв’язування задач на обчислення площі слід мати на увазі такі моменти:
1. Діти повинні достатньо практикуватися у вимірюванні площ прямокутників на моделях та малюнках.
2. Кожен учень має виконати 2—3 завдання на вимірювання площі класної дошки, вікна, поверхні кришки стола, підлоги, стіни класної кімнати, К'мельної ділянки тощо.
Таблиця 33
1 мм[1] — це площа квадрата, сторона якого 1 мм.
1 см2 — це площа квадрата, сторона якого 1 см.
1 дм2 — це площа квадрата, сторона якого 1 дм.
1 м2 — це площа квадрата, сторона якого 1 м.
Ар — це площа квадрата, сторона якого 10 м.
Ар — це сота частина гектара (сотка).
Гектар (га) — це площа квадрата, сторона якого 100 м.
Третій ступінь роботи над задачами цього виду (як і над задачами інших видів) передбачає тривалу практику розв’язування таких задач, творчу роботу над ними.
1 км2 — це площа квадрата, сторона якого 100 м.






