При решении уравнений с модулем используется определение модуля и метод интервалов. Напомним, что 
, если 
.
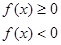Пример 1. Решить уравнение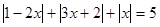 
.
Решение. Приравниваем к нулю выражения, стоящие под знаком модуля, отмечаем на числовой оси полученные значения, исследуем уравнение в каждом из полученных интервалов:
а) если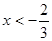 
, то 
и уравнение переписывается так: 
, т.е. 
, 
;
б) если 
, то 
, 
, 
и поэтому имеем 
, и т.к.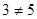 
, то в промежутке 
корней нет;
в) если 
, то получаем 
, т.е. 
, 
; наконец,
г) если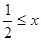 
, то 
, 
, 
.
О т в е т: 
, 
.
Пример 2. Решить уравнение 
.
Решение.
а) 
, тогда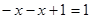 
, 
, 
;
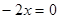б) 
, тогда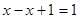 
, 
, 
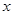- любое из 
;
в) 
, тогда 
, , 
.
О т в е т: 
.
Пример 3. Найти корни уравнения 
.
Решение. Возведя обе части уравнения в квадрат, получим эквивалентное уравнение 
, т.е.
, т.е.
, 
, 
.
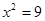О т в е т: 
, 
.
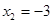Пример 4. решить уравнение 
.
Решение. Это уравнение эквивалентно совокупности систем
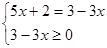и 
Отсюда находим, что 
, 
.
О т в е т: , .
Пример 5. Указать все корни уравнения 
.
Решение. Это уравнение с параметром а. Оно эквивалентно совокупности систем 
и 
.
Находим, что 
, 
, но должно выполняться условие 
, т.е. 
. Стало быть, 
, т.е. 
и 
, т.е. 
.
При 
имеем 
.
О т в е т: если , то 
; если 
, то 
.
З а д а ч и. Решить уравнения.
1) 
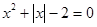
2) 
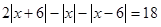
3) 
8. Геометрические задачи
1. Найти смежные углы, если их градусные меры относятся как 3:7.
2. Величины углов треугольника относятся как 1:2:3. Большая сторона имеет длину 8 м. Найти длины меньшей стороны и медианы большей стороны.
Ответ: 4 м,4 м.
3. Средняя линия равнобедренного треугольника, параллельная основанию, равна 6 см. Найти длины сторон треугольника, если его периметр равен 32 см.
4. Из одной точки окружности проведены две взаимно перпендикулярные хорды, которые удалены от центра на 3 см и 5 см. Найти их длины.
5. В равнобочной трапеции большее основание равно 2,7 м, боковая сторона равна 1 м, угол между ними 60 градусов. Найти меньше основание.
Ответ: 1,7 м.
6. Около трапеции описана окружность. Периметр трапеции равен 30 см, а средняя линия равна 9 см. Найти длину каждой из боковых сторон трапеции.
Ответ: 6 см.
7. Сторона треугольника равна 20 см, а противолежащий ей угол 150 градусов. Найти радиус описанной окружности.
Ответ: 20 см.
8. Радиусы вписанной и описанной окружностей прямоугольного треугольника соответственно равны 2 м и 5 м. Найти катеты треугольника.
Ответ: 6 м и 8 м.
9. Даны три стороны треугольника. Найти его углы, если a=55, b=21, c=38.
10. Даны сторона и два угла треугольника. Найти третий угол и остальные две стороны, если c=14, 
, 
.
11. Найти все элементы прямоугольного треугольника с прямым углом С, если известно, что
a) a=6,4; b=50
b) b=65; c=69
c) 
, 
d) a=114,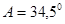 
e) a=18, 
f) 
, 
12. Найдите площадь параллелограмма, если его большая диагональ 5 м, а высота 2 м и 3 м.
13. Найдите площадь трапеции у которой основания 69 см и 20 см, а боковые стороны 13 см и 37 см.
14. Найти стороны ромба, если его диагонали относятся как 3:4, а площадь равна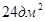 
.
15. Найти площадь равнобедренного треугольника, если его периметр равен 50 дм, а основание меньше боковой стороны на 1 дм.
16. Найти площадь круга, если длина окружности равна 8 м.
Примерное контрольное задание.
Решить уравнение
Решить задачу
С туристической базы вышел пешеход, его скорость 4 км/ч. Через 4,5 ч по той же дороге выехал автомобиль со скоростью 76 км/ч. На каком расстоянии от базы автомобиль догонит пешехода?
3. Постройте график функции 
, записав аналитическое задание функции у:
Вершиной графика является точка М (2;4), и график проходит через точку А (1;5).
Решить задачу
Один из катетов прямоугольного треугольника меньше гипотенузы на 2 см. Сумма трех сторон равна 12 см. Найдите её стороны.
5. Решить графически уравнение: 
10. Основные формулы
1. Свойства степени с рациональным показателем:
; 
;
; 
;
; 
;
; 
.
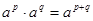
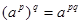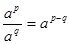
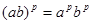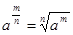
2. Действия с корнями:
; 
; 
;
; 
;
; 
;
; 
;
; 
;
; 
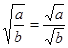
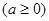Если 
, 
.
Если 
, то 
.
натуральное).
3. Формулы сокращенного умножения:
2 = a2 + 2ab + b2;
(a - b) 2 = a 2 – 2ab + b 2;
3 = a 3 + 3a 2 b + 3ab 2 + b 3;
(a – b) 3 = a 3 - 3a 2 b + 3ab 2 - b 3;
(a + b)(a - b)= a 2 - b 2;
(a + b)(a 2 – ab + b 2 )= a 3 + b 3;
(a - b)(a 2 + ab + b 2 )= a 3 - b 3;
(a – b + c) 2 = a2 + b2 + c 2 – 2ab + 2ac – 2bc;
a2 + b2 = (a + b) 2 – 2ab;
a2 + b2 = (a - b) 2 + 2ab;
4. Квадратное уравнение:
ax2 + bc + c = 0 (a 
0), x1,2 = 
;
ax2 + 2kx + c = 0 (a 0) x1,2 = 
(k2 – ac 
0);
x2 + px + q = 0, x1,2 = 
.
Формулы Виета: 
, 
.
Формулы разложения квадратного трехчлена на линейные множители:
ax2 + bx + c = a(x – x1)(x – x2)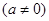 
.
5. Прогрессии:
формула общего члена арифметической прогрессии:
an = a1 + (n - 1)d;
формула суммы первых n членов арифметической прогрессии:
;
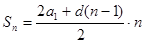формула общего члена геометрической прогрессии:
;
формула суммы первых n членов геометрической прогрессии со знаменателем q 1: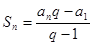 
;
формула суммы бесконечно убывающей геометрической прогрессии:
.
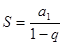
6. Площади многоугольников:
площадь прямоугольника с основанием a и высотой b: S = ab;
площадь параллелограмма с основанием a и высотой h: S = ah;
площадь треугольника с основанием a и высотой h: 
;
площадь треугольника со сторонами a, b, c: 
sin 
, где - угол между сторонами b и c;
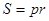, где 
, r – радиус вписанной в треугольник окружности;
, где R – радиус описанной около треугольника окружности;
формула Герона: 
, где ;
площадь трапеции с основаниями a, b и высотой h: 
;
площадь правильного многоугольника: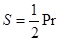 
, где P – периметр многоугольника, r – радиус вписанной в него окружности;
площадь правильного n -угольника: 
sin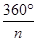 
, где R – радиус описанной окружности.
Сторона правильного n -угольника:
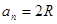sin 
; 
cos ;
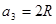sin 
; 
sin 
; 
sin 
.
7. Окружность, круг:
длина окружности: C = pD = 2pR;
длина дуги окружности, отвечающая центральному углу в 
: 
;
площадь круга: S =pR2;
площадь кругового сектора: 
;
площадь сегмента с радианной мерой центрального угла a: 
.
Литература
1. Вавилов В.В. и др. Задачи по математике. Начала анализа. – М.: Наука, 1990
2. Вавилов В.В. и др. Задачи по математике. Алгебра. – М.: Наука, 1989.
3. Вавилов В.В. и др. Задачи по математике. Уравнения и неравенства. – М.: Наука, 1989.
4. Нестеренко Ю.В. и др. Задачи вступительных экзаменов по математике. – М.: Наука, 1983
5. Сборник конкурсных задач по математике для поступающих во втузы / Под редакцией Сканави М.И. – М.: Высшая школа, 1980.
6. Цыпкин А.Г. Справочник по математике. – М.: Наука, 1983.
