Усі випадки множення і ділення, що виходять за межі таблиць умовно названі "поза табличними", і розглядаються на прикладі чисел в межах 100, а узагальнюються на числах в межах 1000. Однак сама тема "Усне множення і ділення" пропонується в рамках розділу "Множення і ділення в межах 1000".
Тема вивчається в наступному порядку:
1. Множення і ділення з числами 0, 1, 10, 100.
2. Множення і ділення розрядних чисел на одноцифрове число.
3. Ділення числа на добуток. Ділення виду 80: 20, 600: 30.
4. Множення суми на число і числа на суму. Множення виду 24 -3,4 «21, 320-3.
5. Ділення суми на число. Ділення виду 39: 3, 72: 6. Перевірка ділення і множення. Ділення виду 64: 16,125: 25.
7. Ділення з остачею.
Різноманітні випадки множення і ділення вводяться після вивчення відповідних властивостей арифметичних дій. Це обумовлено тим, що прийоми поза табличного множення і ділення побудовані на властивостях:
Ділення числа на добуток: розділити число на добуток можна тким способом - спочатку розділити число на один із множників, а потім результат поділити на інший множник:
a: (b * c) = a: b:c
a: (b * c) = a: c: b
Множення суми на число: щоб помножити суму на число, можна помножити кожний добуток на це число, і отримані добутки додати
(a + b) * c = a * c + b * c
Множення числа на суму: щоб помножити число на суму, можна помножити це число на кожний доданок, і отримані добутки додати
c * (a + b) = c * a + c * b
Ділення суми на число: щоб розділити суму на число, можна розділити кожний доданок на це число, і отримані частки додати
(a + b): c = a: c + b: c
В результаті вивчення теми учні оволодівають уміннями і навичками:
Знати і вміти застосовувати правила:
Множення будь-якого числа на одиницю або нуль;
Ділення будь-якого числа на одиницю;
Ділення будь-якого числа само на себе;
Ділення нуля на будь-яке число;
Неможливість ділення на нуль;
Множення будь-якого числа на 10 чи 100.
Знати властивості арифметичних дій множення і ділення:
А) множення суми на число;
Б) ділення суми на число;
В) ділення числа на добуток;
і вміти ними користуватися при усних обчисленнях.
Засвоїти прийоми усних обчислень в межах 100: знати і вміти:
А) множити і ділити розрядне число на одноцифрове;
Б) ділити розрядне число на розрядне;
В) множити двоцифрове число на одноцифрове;
Г) ділити двоцифрове число на одноцифрове;
Д) ділити двоцифрове число на двоцифрове.
4. Вміти виконувати усне ділення з остачею.
Як теоретичне забезпечення прийомів обчислення розглядають ділення числа на добуток, множення суми на число і число на суму, ділення суми на число. Основне завдання множення і ділення багатоцифрових чисел полягає у формуванні навичок письмового множення і ділення. Учні повинні вміти пояснювати виконання дій. Треба систематизувати знання учнів про дії множення і ділення та їхні властивості.
Алгоритми дій множення і ділення різні. Тому прийоми виконання дій вводять почергово: після вивчення одного випадку множення вивчають аналогічний випадок ділення. Опрацювання матеріалу має таку послідовність:
множення і ділення на одноцифрове число;
множення і ділення на дво- і трицифрові розрядні числа;
множення і ділення на двоцифрове число [10, 27].
20. Письмове множення на одноцифрове число. Послідовність розгляду випадків множення визначається зростанням їх складності: 213 • 3 = 639 (множення (>с:і переходу через розряд); 37 • 6 = 222, 127 • 3 = 381 (множення з переходом через розряд); 151 • 6 = 906 (у добутку нуль); 125 • 4 = 500 (у добутку два нулі). І Іотім учні вчаться застосовувати набуті вміння для обчислення виразів на
сумісні дії.
Підготовча робота до вивчення письмового множення має бути реалізо-папа в процесі виконання таких завдань: заміна дії додавання множенням, і навпаки; множення з 0 і 1; множення розрядних чисел на одноцифрове число; застосування властивості множення суми на число до множення ниду 14 • 3; розв'язування вправ виду (7 + 6 + 2) ■ 3.
Перехід від усного множення до письмового треба здійснити так, щоб учні усвідомили необхідність вивчення письмового множення (з цією метою учням потрібно запропонувати текстову задачу практичного змісту).
Пояснення. При письмовому множенні другий множник записуємо під першим. Розмістити числа треба так, щоб одиниці другого множника були шписані під одиницями першого. Розглянемо приклад. 312
х_з
При письмовому множенні починають множити з одиниць: множимо па 3 спочатку 2 од., потім 1 дес. і, нарешті, 3 сот.
2 од. помножити на 3, буде 6 од. Пишемо цифру 6 під одиницями. 1 дес. помножити на 3, буде 3 дес. Пишемо цифру 3 під десятками. З сот. помножити на 3, буде 9 сот. Пишемо цифру 9 на місці сотень. У добутку отримали число 936.
У процесі закріплення на цьому уроці діти обчислюють два вирази з коментуванням (з них один виду 103 • 3), а два-три вирази — самостійно за
паріантами.
Від докладного пояснення обчислення виразів такого виду учні переходять до короткого пояснення. Наведемо зразки докладного і короткого пояснення множення двоцифрового числа на одноцифрове з переходом через розряду
39 127
х 6х З
234 381192
' Розділ VIII. Нумерація чисел 101-1000. Арифметичні дії в межах 1000
Докладне пояснення. Множимо 9 од. на 6, буде 54 од. Це 5 дес. і 4 од.; 4 од. пишемо під одиницями, а 5 дес. запам'ятовуємо; 3 дес. помножити на 6, буде 18 дес. та ще 5 дес, буде 23 дес. Це 2 сот. і 3 дес. Отримаємо 234.
Коротке пояснення. Множимо 7 на 3, буде 21; 1 пишемо, а 2 запам'ятовуємо;
2 множимо на 3, буде 6 та ще 2, буде 8. 1 помножити на 3, буде 3. Пишемо 3. Всього маємо 381.
Письмове ділення на одноцифрове число. Алгоритм письмового ділення складається з багатьох операцій: перетворення одиниць вищого розряду на одиниці нижчого розряду, табличне ділення, ділення з остачею, множення, віднімання. Ці операції мають стати предметом підготовчої роботи. Велику увагу слід приділити повторенню випадків ділення з одиницею і нулем, перевірці ділення множенням.
Письмове ділення на одноцифрове число вивчають у такій послідовності: 966: 3 = 322; 864: 4 = 216; 276: 4 = 69; 822: 6 = 137; 618: 3 = 206. Варто також обчислити кілька виразів на сумісні дії, однією з яких є ділення на одноцифрове число.
Випадок виду 966: 3 розглядають без детального коментування; туї' головною є форма запису, розміщення компонентів письмового ділення. На наступному уроці подається детальне коментування ділення виду 864: 4.
Ми відразу подаємо пояснення для випадку письмового ділення, коли її частці буде двоцифрове число.
При усному діленні ми розкладали ділене на зручні доданки і потім ділили на 3 кожний доданок окремо. При письмовому діленні також розкладають ділене на зручні доданки. Проте спочатку знаходять неповні ділені — цс числа, які попередньо виділяють із діленого, щоб відшукати цифру частки.
Розгляньмо детальне пояснення процесу ділення на прикладі 276: 4.
276 ' '
24_
36_ ■; ■
Докладне пояснення. Ділене — 276, дільник — 4. Утворюємо перше неповне ділене. Вищий розряд діленого — сотні. 2 сот. не можна поділити на 4 так, щоб у результаті отримати сотні.
Замінимо 2 сот. десятками і додамо 7 дес, отримаємо 27 дес. Це перше неповне ділене. Отже, вищий розряд частки — десятки. У частці буде дві цифри. Позначимо їх місце крапками.
27 дес. поділимо на 4, буде 6 дес. Запишемо цифру 6 у частці на місці десятків. Визначимо, скільки всього десятків поділили. Помножимо 6 дес. на 4, буде 24 дес. Запишемо 24 дес під 27 дес. діленого, тобто під першим неповним діленим і підведемо риску. Віднімемо 24 дес. від 27 дес, буде
3 дес; 3 дес. не можна поділити на 4 так, щоб отримати десятки. Отже, цифру 6 знайдено правильно.
Утворимо друге неповне ділене. До остачі додамо 6 од. діленого; 3 дес. і Ь од., буде 36 од. Поділимо 36 од. на 4, буде 9 од. Запишемо цифру 9 у частці ми місці одиниць. Визначимо, скільки одиниць поділили. Помножимо 9 од. на 4, буде 36 од. Запишемо 36 од. під другим неповним діленим і підведемо риску. Віднімемо 36 від 36, буде 0. Одиниці поділили всі. Частка — 69.
У 4 класі повторюємо докладне пояснення алгоритму ділення на одпоцифрове число і вводимо коротке пояснення, яким користуємось надалі.
Розглянемо алгоритм ділення для найскладнішого випадку, коли в записі чистки всередині є нуль.
Докладне пояснення. Ділене — 618, дільник — 3. Утворимо перше неповне ділене. Вищий розряд діленого — сотні. 6 сот. діляться на 3, тому вищим розрядом частки будуть сотні. Отже, в частці буде три цифри. Позначимо місця цих цифр крапками.
618 ІЗ
і 6_ [ІС
_
6 сот. — перше неповне ділене. Поділимо 6 сот. на 3, буде 2 сот. Запишемо цифру 2 у частці на місці сотень. Перевіримо, скільки сотень ми поділили.
1 Іомножимо 2 сот. на 3, буде 6 сот. Запишемо цифру 6 під сотнями діленого. Піднімемо 6 сот. від 6 сот., буде 0. Усі сотні поділили.
1 дес. — це друге неповне ділене. 1 дес. не можна поділити на 3 так, щоб отримати десятки. Тому в частці на місці десятків запишемо 0.
Утворимо третє неповне ділене. 1 дес. і 8 од. буде 18 од. Поділимо 18 од. па 3, буде 6 од. Запишемо цифру 6 у частці на місці одиниць. Визначимо, скільки одиниць поділили. Помножимо 6 од. на 3, буде 18 од. Запишемо 18 од. під третім неповним діленим 18 од. Віднімемо 18 від 18, буде 0. Запишемо 0 під рискою. Усі одиниці поділили. Всього у частці отримаємо 206.
Коротке пояснення. Перше неповне ділене — 6 сот. Отже, вищим розрядом чистки будуть сотні, тому в частці буде три цифри. 6 сот. поділити на 3, буде
2 сот. Остачі немає.
Друге неповне ділене — 1 дес. Його не можна поділити на 3 так, щоб отримати десятки. Тому в частці на місці десятків буде 0.
Третє неповне ділене — 18 од. 18 од. поділити на 3, буде 6 од. Остачі немає. Частка — 206.
Наведені зразки пояснень свідчать про складність алгоритму письмового ділення. Засвоєння його викликає в учнів значні труднощі. Певну допомогу її їх подоланні може надати така нам 'ятка письмового ділення:
1. Виділіть перше неповне ділене і встановіть кількість цифр у частці.
2. Знайдіть першу цифру частки, дізнайтеся, скільки одиниць першого неповного діленого поділили і скільки залишилось поділити.
3. Утворіть друге неповне ділене і продовжуйте ділення, поки не розв'яжете приклад до кінця,.,.,. 194
Розділ VIII. Нумерація чисел 101-1000. Арифметичні діївмежщх 1000
Множення і ділення на двоцифрове число к,>«т
Тема "Письмове множення двоцифрового числа на двоцифрове".7 ■, Бесіда. Будемо вчитися множити двоцифрові числа. Спробуємо спочатку обчислити добуток 23 • 42 усно, але за розгорнутим записом:
23 • 42 = 23 • (40 + 2) = 23 • 40 + 23 • 2 =■ і) = 23 • 4 • 10 + 23 • 2 = 920 + 46 = 966.
■ Без такого запису знайти добуток двоцифрових чисел важко. Будемо застосовувати письмовий спосіб.
Пояснення нового матеріалу.
Докладне пояснення. При письмовому множенні на двоцифрове число спочатку множать на одиниці, а потім на десятки. Нам треба 23 помножити спочатку на 2, а потім на 40, або 4 дес.
Х 12
92_
Множимо 23 на 2 од. і в результаті отримаємо одиниці, тому результат починаємо записувати під одиницями. З помножити на 2, буде 6, запишемо цифру 6 під одиницями; 2 помножити на 2, буде 4. 46 — перший неповний добуток.
Множимо 23 на 4 дес. і в результаті отримаємо десятки, тому результат починаємо записувати під десятками. З помножити на 4, буде 12; запишемо цифру 2 під десятками, а 1 запам'ятаємо; 2 помножити на 4, буде 8. До 8 додаємо 1, матимемо 9. 92 дес. — другий неповний добуток.
Додамо неповні добутки й отримаємо остаточний результат 966.
Коротке пояснення. При письмовому множенні спочатку множать на одиниці, а потім на десятки.
23 помножити на 2 од., буде 46. Це перший неповний добуток, його записують так, щоб остання цифра була розміщена під одиницями.
23 помножити на 4 дес, буде 92 дес. Це другий неповний добуток, його записують так, щоб остання цифра була розміщена під десятками.
Додамо неповні добутки, отримаємо 966. У процесі роботи потрібно звертати увагу учнів, що другий неповний добуток виражає десятки.
Тема "Ділення трицифрового числа на двоцифрове у випадку одно-цифрової частки".
Пояснення. Ділене — 144, дільник — 24. 14 менше, ніж 24, отже, будемо ділити відразу 144 на 24. У частці буде одна цифра. Частку шукаємо способом випробовування. Пробну цифру можна швидше знайти, якщо 14 дес. поділимо на число десятків дільника: 14:2 = 7. Перевіримо цифру 7 усно: 20 • 7 = 140, 4 • 7 = 28, сума чисел 140 і 28 більша, ніж 144. Цифра 7 не підходить. Перевіримо цифру 6. 20 • 6 = 120, 4 ■ 6 = 24, сума чисел 120 і 24 дорівнює 144. Отже, цифра 6 правильна. Запишемо у частку цифру 6.
Як закріплення учні з поясненням знаходять частку 196: 28, а потім один-два приклади розв'язують самостійно з подальшим фронтальним пояс-
Методжа викладання математики в початкових класах
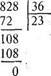
пенням. І нарешті, розглядають ділення трицифрового числа на двоцифрове у випадку двоцифрової частки.
Докладне коментування. Перше неповне ділене — 82 дес. Отже, вищим розрядом частки будуть десятки. Тому в частці буде дві цифри.
Дізнаємося, скільки десятків буде в частці. Для цього 82 дес. поділимо на 36. Можна взяти по 2. Дізнаємося, скільки десятків поділили. Для цього 2 дес. помножимо на 36. Буде 72 дес. Дізнаємося, скільки десятків ще не поділили. Для цього від 82 дес. віднімемо 72 дес. Залишилось 10 дес.
Утворимо друге неповне ділене. 10 дес. — це 100 од. та ще 8 од. діленого — буде 108 од. Дізнаємося, скільки одиниць буде в частці. Для цього 108 поділимо на 36. Можна взяти по 3. Помножимо 36 на 3, щоб дізнатись, скільки одиниць поділили. Буде 108. Поділили всі одиниці. Остачі немає. Частка — 23.
Для закріплення варто запропонувати пояснити кілька розв'язань такими завданнями:
1. Назвіть перше неповне ділене.
2. Розкажіть, як знайти першу цифру частки.
3. Назвіть друге неповне ділене.
4. Розкажіть, як знайти другу цифру частки.
У процесі закріплення та розв'язування задач виконують дії над Іменованими числами, вираженими у метричних мірах. При виконанні арифметичних дій у більшості випадків замінюють складене іменоване число простим і виконують дії над відповідними абстрактними числами, а потім результат перетворюють на складене іменоване число.






