1. Лінійне однорідне диференціальне рівняння надалі (ЛОДР) другого порядку зі сталими коефіцієнтами має вигляд:
(1)
Функція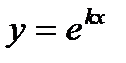 
є розв’язком даного рівняння 
, 
,
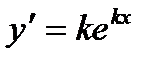де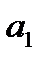 
; 
; 
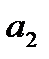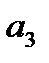- сталі, причому 
. 
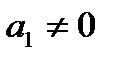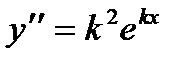, підставивши значення 
, 
, 
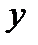в рівняння (1), одержимо:
|: 
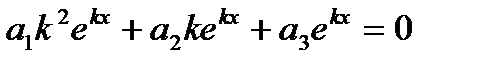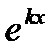
(2)
Дане рівняння називають характеристичним рівнянням ЛОДР.
2. Якщо характеристичне рівняння (2) має два дійсні розв’язки 
, то загальний розв’язок ЛОДР (1) буде:
(3)
3. Якщо характеристичне рівняння (2) має один дійсний корінь k (в такому випадку кажуть, що воно має два дійсні корені, рівні між собою), то загальний розв’язок цього ЛОДР буде:
.
4. Якщо характеристичне рівняння (2) не має дійсних коренів, то воно має два спряжені комплексні корені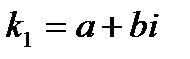 
, 
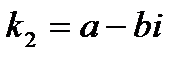, де а, b – дійсні числа, і – уявна одиниця (і 
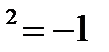). Тоді загальним розв’язком ЛОДР (1) буде:
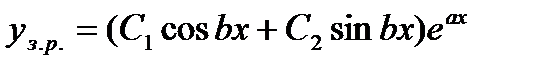
Задача 1. Знайти загальний розв’язок диференціального рівняння
.
Задача 2. Знайти загальний розв’язок диференціального рівняння
.
Задача3. Дано диференціальне рівняння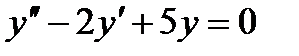 
. Знайти:
а) загальний розв’язок рівняння;
б) частковий розв’язок, що задовольняє початкові умови: y(0)=0 та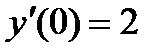 
.
Питання для самоконтролю знань, умінь
1. Загальний вигляд лінійного диференціального рівняння другого порядку з сталими коефіцієнтами.
2. Зміст характеристичного рівняння.
3. Випадки загального розв’язку диференціального рівняння з сталими коефіцієнтами в залежності від значення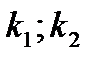 
4. Задача Коші для диференціальних рівнянь другого порядку з сталими коефіцієнтами.
Висновок.______________________________________________________________
Перевірив викладач ___________ Оцінка ___________ Дата___________
