Мета роботи: навчитись знаходити найбільше та найменше значення функції на відрізку та розв’язувати прикладні задачі на застосування похідної.
Наочне забезпечення та обладнання:
1. Інструкційні картки;
2. Приклади задач;
3. Роздаткові матеріали: опорні конспекти «Основні формули диференціювання», варіанти завдань
4. Обчислювальні засоби: калькулятор.
Теоретичні відомості про найбільшеі найменше значення функції на проміжку
Найбільше і найменше значення монотонної функції 
на відрізку 
знаходиться на кінцях відрізка. Якщо ж задана функція не являється монотонною на відрізку 
, але відомо, що вона неперервна, то для знаходження найбільшого і найменшого значення функції на відрізку необхідно:
1. Зайти критичні точки функції.
2. Знайти значення функції в критичних точках, які належать відрізку, і на кінцях відрізку. Найбільше і найменше значення з цих чисел і будуть відповідно найбільшим і найменшим значення функції на відрізку.
Задача № 1. Знайти найбільше і найменше значення функції: 
Теоретичні відомості про екстремум функції
Теорема (друге правило). Якщо в точці 
похідна 
функції 
дорівнює нулю, а її друга похідна 
неперервна в околі цієї точки і 
, то функція має максимум в точці , коли 
і мінімум, коли 
.
Задача №2. Знайти максимум і мінімум функції 
Задача №3. Знайти довжини сторін прямокутника з периметром 72 см, що має найбільшу площу.
Теоретичні відомості про застосування похідної
1. Фізичний зміст похідної. При прямолінійному русі точки швидкість в даний момент 
дорівнює похідній 
від шляху 
по часу 
, обчисленій при : 
.
Прискорення 
в даний момент дорівнює похідній 
від швидкості 
по часу 
, обчисленій при : 
.
2. Геометричний зміст похідної. Похідна 
дорівнює кутовому коефіцієнту 
дотичної до кривої, проведеної у точці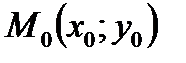 
. Рівняння дотичної до графіка функції 
в точці з абсцисою 
має вигляд: 
.
Задача №4. Знайти швидкість і прискорення точки, що рухається за законом 
в момент часу 
.
Задача №5. Скласти рівняння дотичної до графіка функції 
в точці з абсцисою 
.
Питання для самоконтролю знань, умінь
1. Які точки називаються критичними?
2. Правило знаходження найбільшого та найменшого значення функції.
3. Які точки називаються точками максимуму і точками мінімуму?
4. Перше правило відшукання екстремуму функції.
5. Друге правило відшукання екстремуму функції.
6. Фізичний зміст похідної.
7. Геометричний зміст похідної. Рівняння дотичної до графіка функції.
Висновок __________________________________________________________
____________________________________________________________________
Перевірив викладач_________________ Оцінка _________Дата________
<
Дата добавления: 2015-10-20; Мы поможем в написании ваших работ!; просмотров: 955 | Нарушение авторских прав Поиск на сайте: Лучшие изречения:  | 2320 -  |
Ген: 0.012 с.